Matematika

Matematika (z gr. μαθηματικός (mathematikós)= „milujúci poznanie“ > μάθημα (máthema) = „veda, poznanie“) je väčšinou definovaná ako štúdium zákonitostí štruktúry, zmeny a priestoru. Neformálne ju môžeme tiež nazvať štúdiom „diagramov a čísel“. Z formálneho hľadiska je matematika skúmanie axiomaticky definovaných formálnych štruktúr použitím logiky a matematického označenia. Matematiku možno chápať jednoducho ako rozšírenie hovoreného a písaného jazyka s veľmi presne definovanou slovnou zásobou a gramatikou, s cieľom opisovať a skúmať fyzikálne a konceptuálne vzťahy.

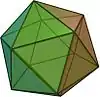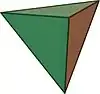
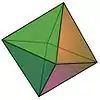
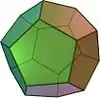
Niektoré platónske telesá tak ako ich poznala už staroveká geometria.

Hoci matematika samotná sa väčšinou nepovažuje za prírodnú vedu, špecifické štruktúry skúmané matematikmi majú často pôvod v prírodných vedách, najmä vo fyzike. Matematici sa však zaoberajú aj štruktúrami, ktorých pôvod nie je čisto matematický, napríklad ak poskytujú zovšeobecnenie spájajúce niekoľko odborov alebo zjednodušujú výpočty. Mnohí matematici sa zaoberajú určitými problémami z čisto estetických dôvodov, chápajúc matematiku skôr ako umenie než praktickú, alebo aplikovanú vedu. Niektorí matematici nazývajú matematiku „kráľovnou vied“.

Prehľad a história matematiky

Hlavné odvetvia matematiky vznikli z potreby robiť výpočty pre účely obchodu, merať pozemky a predpovedať astronomické udalosti. Tieto tri potreby približne zodpovedajú rozdeleniu matematiky na štúdium štruktúry, priestoru a zmeny.

Štúdium štruktúry začína pojmom čísla. Najskôr boli známe prirodzené a celé čísla a ich aritmetické operácie, ktoré sú zahrnuté v elementárnej algebre. Zložitejšie vlastnosti celých čísel skúma teória čísel. Skúmanie metód na riešenie rovníc viedlo k vzniku abstraktnej algebry, ktorá okrem iného skúma štruktúry ako okruhy a polia, ktoré zovšeobecňujú vlastnosti dobre známych aritmetických operácií na číslach. Vektor je pojem dôležitý vo fyzike. Lineárna algebra, ktorá študuje vektory a ich zovšeobecnenie, vektorové priestory, sa nachádza na priesečníku štúdia štruktúry a priestoru.

Štúdium priestoru vychádza z geometrie. Najskôr sa rozvíjala euklidovská geometria a trigonometria dobre známeho trojrozmerného priestoru. Neskôr bola euklidovská geometria zovšeobecnená na neeuklidovské geometrie, ktoré majú dôležitú úlohu v všeobecnej teórii relativity. Niekoľko ťažkých geometrických problémov týkajúcich sa konštrukcií pomocou pravítka a kružidla bolo vyriešených pomocou Galoisovej teórie. Moderné odvetvia diferenciálnej a algebrickej geometrie rozširujú geometriu v nových smeroch. Diferenciálna geometria sa sústredí na pojmy funkcie, derivácie a smeru, kým algebrická geometria definuje geometrické objekty ako množiny riešení polynomiálnych rovníc. Teória grúp skúma pojem symetrie, spája štúdium priestoru a štruktúry. Topológia spája štúdium priestoru a zmeny s dôrazom na koncept kontinuity.

Prírodné vedy často skúmajú zmenu merateľných veličín a matematická analýza na to poskytuje užitočné nástroje. Základným pojmom používaným na popísanie zmeny je pojem funkcie. Mnohé problémy sa dajú vyjadriť ako vzťah medzi veličinou a rýchlosťou jej zmeny. Metódy na riešenie takýchto vzťahov skúma odbor diferenciálnych rovníc. Spojité veličiny sú reprezentované reálnymi číslami. Vlastnosti reálnych čísel a funkcií nad reálnymi číslami skúma reálna analýza. Z viacerých príčin sa často hodí pracovať s komplexnými číslami, ktoré študuje komplexná analýza. Funkcionálna analýza sa zaoberá priestormi funkcií, ktoré majú väčšinou nekonečne veľa rozmerov. Toto štúdium poskytuje okrem iného matematický základ kvantovej mechaniky. Teória chaosu vznikla z dôvodu, že mnohé z prírodných javov tvoria dynamické systémy, ktoré majú nepredpovedateľné ale deterministické správanie.

Teória množín, matematická logika a teória modelov vznikli s cieľom skúmať základy matematiky.

Keď vznikla myšlienka počítačov, matematici zaviedli niekoľko dôležitých teoretických pojmov, ktoré viedli k vzniku odborov ako teória vypočítateľnosti, teória výpočtovej zložitosti, teória informácie a algoritmická teória informácie. Tieto odbory sú dnes časťou teoretickej informatiky. Diskrétna matematika je spoločné meno pre odbory matematiky obzvlášť užitočné v informatike.

Dôležitým odborom aplikovanej matematiky je štatistika, ktorá používa teóriu pravdepodobnosti ako nástroj na opis, analýzu a predpoveď javov a používa sa vo všetkých vedách. Numerická analýza skúma metódy na efektívne riešenie rôznych matematických problémov na počítačoch a zaokrúhľovacie chyby, ktoré pri numerickom riešení vznikajú.

Matematické disciplíny

Tu uvedený zoznam matematických disciplín vonkoncom nemožno považovať za úplný. Záujemcov o naozaj hlboký pohľad do členenia matematických disciplín a ich poddisciplín možno odkázať na AMS Mathematics Subject Classification[1], čo je hierarchia matematických disciplín udržiavaná a aktualizovaná Americkou matematickou spoločnosťou.

Názory filozofov na matematiku

Aristoteles

Matematika je podľa Aristotela veda, ktorá predpokladá kategórie jedného a mnohého.

Cassirer

Matematika podľa Ernsta Cassirera sa má zaoberať len a výlučne vystihovaním a predstavovaním funkcií vzťahov a závislostí. Matematika nie je vedou týkajúcou sa kvantity.

Descartes

René Descartes mal na matematiku takýto názor: Dlhé reťaze výpočtov celkom jednoduché a ľahké, ktoré geometri obyčajne používajú k svojim najťažším demonštráciám, mi vnukli myšlienku, že všetky veci ľuďmi poznateľné idú za sebou v rovnakom poradí a že niet takých vecí, ku ktorým by sa napokon nedospelo, ani takých skrytých, ktoré by sa neodhalili, ak, pravda, neprijmeme klamnú vec za pravdivú a vždy zachovávame patričné poradie, aby sme mohli odvodiť jednu z druhej.

Novoveká filozofia

Novoveká filozofia má na matematiku takýto názor: Klasická filozofia predstavovala matematiku ako vzor metodického myslenia, chápala ju ako sféru evidentných, jasných a zreteľných ideí. Práve tak sa za jasné a prehľadné považujú súvislosti medzi východiskovými princípmi (axiómami) a vetami odvodenými z týchto východísk pomocou jasne a zreteľne stanovených pravidiel.

Filozofia

Podľa filozofie je rozhodujúcou vetou o podstate matematiky z filozofického hľadiska Gödelova veta o neúplnosti.

Frege

Gottlob Frege mal na matematiku takéto názory: Aritmetická pravda nie je syntetická, ale analytická v zmysle zákonov logiky natoľko elementárnych, že ich nemožno poprieť bez protirečení. Gottlob Frege bol vlastne "platonikom"; veril vo sféru matematickej pravdy, nezávislej od ľudskej schopnosti získavať o nej poznanie. Napriek tomu z jeho myšlienok sa zanedlho utvorila matematická veda, nie však ako objavovanie ríše nadčasových entít, ani ako prvoradý príklad syntetického apriórneho poznania, ale ako prienik do logického priestoru nášho vlastného sklonu ku koherentnému mysleniu. Čo sa javí ako nezávislá sféra matematických entít alebo matematickej pravdy, to je jednoducho tieňová reprezentácia našich vlastných intelektuálnych schopností. Číslo jedna nie je o nič viac entitou ako priemerný človek a zákony matematiky nie sú o nič väčšmi pravdami o nezávislom svete ako výrok, že "všetci starí mládenci sú neženatí". Ak matematickú pravdu poznáme a priori, tak preto, že sme sami tú pravdu konštruovali. (Toto vysvetlenie apriórneho poznania je staré a pochádza od stredovekých nominalistov, ktorým chýbali prostriedky, aby mohli určiť, či sa dá aplikovať na matematiku.) G. Frege prvý rozvinul logiku, v ktorej by sa dala posúdiť a dokázať teória aritmetiky Podľa Fregeho Kantova teória matematiky, teda že každá matematická pravda je syntetická a priori, je omyl. Tento omyl sa dá dokázať, ak sa prijme logika bez aristotelovských predpokladov, ktoré hypnotizovali Kanta.

Mill a Frege

Pre Milla sú naše idey čísiel odvodené zo skúsenosti. Číslo tri je nám dobre známe z vnímania trojitosti, štyri z vnímania štvoritosti a tak ďalej. Na matematické pravdy samy, ako napríklad 2+3=5, možno hľadieť aj tak, že odrážajú najzákladnejšie zákony prírody, čo sa odpozorovalo ako niečo, čo dominuje zoskupeniam, na ktoré sa vyťahuje. Gottlob Frege vo svojich Základoch aritmetiky (1884) tvrdil, že tento výklad podstaty čísiel nemožno prijať |K1|takisto ako iný výklad o nich. J.S. Mill nám nielenže nedáva kľúč k pochopeniu nuly, ale hranice nášho matematického poznania vymedzuje aj ako hranice našej skúsenosti. Ale kto skutočne chce potvrdiť fakt, ktorý je podľa Milla obsiahnutý v definícii osemnásťmiestneho čísla, že sa vôbec kedy stalo predmetom pozorovania, a kto chce poprieť, že napriek tomu má symbol takéhoto čísla zmysel? Keď John Stuart Mill tvrdí, že zákony aritmetiky sú induktívne zovšeobecnenia, pletie si používanie matematiky s matematikou samou. Matematika je zrozumiteľná nezávisle od svojho používania. G. Frege napokon vyzdvihuje, že indukcia sa musí zakladať na teórii pravdepodobnosti, lebo nikdy nemôže postihnúť výrok väčšmi ako pravdepodobne. Nedá sa však pochopiť, ako by sa teória pravdepodobnosti dala rozvinúť bez predpokladu zákonov aritmetiky. Na Milla reaguje aj Edmund Husserl.

Tarski

Matematika podľa Alfreda Tarskeho je vedecká teória, ktorej tvrdenia (teorémy, vety) vyplývajú jedno z druhého v určitom poradí podľa istých princípov a sú spravidla sprevádzané dôkazmi. Medzi termínmi a symbolmi vyskytujúcimi sa v matematických teorémach a dôkazoch rozlišujeme konštanty a premenné. Každý z týchto termínov má presne vymedzený význam, ktorý v priebehu úvah zostáva nemenný. Ako premenné sa spravidla používajú jednotlivé písmená. Na rozdiel od konštánt nemajú samé osebe nejaký význam. Také výrazy, ktoré obsahujú premenné a stanú sa výrokmi, keď tieto premenné nahradíme konštantami, sa nazývajú výrokové funkcie. Výrokové funkcie a výroky, ktoré sa skladajú výlučne z matematických symbolov (a nie zo slov bežného jazyka), matematici označujú ako formuly. Matematika ďalej obsahuje označovacie alebo deskriptívne funkcie, ktoré sú výrazmi meniacimi sa po nahradení premenných konštantami na označenie (opis) vecí. Medzi deskriptívne funkcie patria všetky tzv. algebrické výrazy, ktoré sa skladajú z premenných, numerických konštánt a symbolov štyroch základných aritmetických operácií. Algebrické funkcie, t. j. formuly skladajúce sa z dvoch algebrických výrazov spojených symbolom =, sú výrokové funkcie. Premenné, ktoré sa vyskytujú v rovniciach, sa hovorieva ako o neznámych, a o číslach, ktoré spĺňajú rovnicu, ako o koreňoch rovnice. Najdôležitejšie teorémy matematiky sú formulované ako všeobecné výroky alebo výroky všeobecného charakteru, ktoré tvrdia, že akákoľvek vec určitej kategórie (napr. v prípade aritmetiky ľubovoľné číslo) má takú a takú vlastnosť. Vo formulácii všeobecných výrokov sa používa obrat pre akékoľvek veci (alebo čísla) x, y,...; tento obrat sa však často vypúšťa a musíme si ho myšlienkovo doplniť. V matematike sa vyskytujú aj existenčné výroky alebo výroky existenčného charakteru, ktoré konštatujú existenciu vecí (napr. čísel), ktoré majú určitú vlastnosť. Vo formulácii existenčných výrokov sa používa obrat existujú čísla x a y také, že…, alebo pre niektoré čísla x a y,.... V matematike sa ďalej vyskytujú výroky, ktoré neobsahujú nijakú premennú; tieto sa označujú ako singulárne výroky alebo jedinečné výroky. V matematike ďalej existujú podmienené existenčné výroky alebo absolútne existenčné výroky, ktoré konštatujú, že čísla majúce určitú vlastnosť existujú, ale za podmienky, že existujú niektoré iné čísla. Premenná sa delia voľné premenné a viazané premenné. Zavedeniu premenných vďačíme za rozvoj metódy takej plodnej pre riešenie matematických problémov, akou je metóda rovníc. Vynález premenných znamenal bod obratu v dejinách matematiky; týmito symbolmi získal človek nástroj, ktorý pripravoval cestu obrovskému rozvoju matematickej vedy a upevneniu jej logických základov. Veda o matematike sa nazýva metamatematika.

Referencie
Matematický portál
  1. 2010 Mathematics Subject Classification

Iné projekty
  • Wikicitáty ponúkajú citáty od alebo o Matematika
  • Commons ponúka multimediálne súbory na tému Matematika

Externé odkazy
  • FILIT – zdroj, z ktorého pôvodne čerpal tento článok.
  • FILIT – zdroj, z ktorého pôvodne čerpal tento článok.
  • FILIT – zdroj, z ktorého pôvodne čerpal tento článok.
  • FILIT – zdroj, z ktorého pôvodne čerpal tento článok.
  • FILIT – zdroj, z ktorého pôvodne čerpal tento článok.
  • FILIT – zdroj, z ktorého pôvodne čerpal tento článok.
  • FILIT – zdroj, z ktorého pôvodne čerpal tento článok.
  • FILIT – zdroj, z ktorého pôvodne čerpal tento článok.
  • FILIT – zdroj, z ktorého pôvodne čerpal tento článok.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.