Hermitovy polynomy

Hermitovy polynomy jsou v matematice klasická ortogonální řada polynomů.

Hermitovy polynomy se objevují:

ve zpracování signálu jako Hermitovské vlnky pro analýzu vlnkovou transformací
v pravděpodobnosti, jako například Edgeworthova řada nebo v souvislosti s Brownovým pohybem;
v kombinatorice, jako příklad Appellovy posloupnosti, která řídí stínový počet;
v numerické matematice jako Gaussovo kvadraturní pravidlo;
ve fyzice, kde způsobují kvantové stavy kvantového harmonického oscilátoru;
v teorii systémů ve spojení s nelineárními operacemi na Gaussovském šumu.
v náhodných maticích v Gaussovských náhodných maticích.

Hermitovy polynomy definoval Pierre-Simon Laplace v roce 1810,[1][2] i když v sotva rozpoznatelném formě, a detailně je zkoumal Pafnutij Lvovič Čebyšev v roce 1859.[3] Čebyševova práce byla přehlížena a polynomy byly pojmenovány později po Charlesu Hermitovi, který je popsal jako nové v roce 1864.[4] Polynomy tedy nebyly zcela nové, ale Hermite byl první, kdo definoval vícerozměrné polynomy ve své pozdějším díle z roku 1865.

Definice

Hermitovy polynomy je možné definovat stejně jako jiné klasické ortogonální polynomy několika způsoby. Je třeba si uvědomit, že se používají dvě různé standardizace, přičemž pohodlná metoda je tato:

„pravděpodobnostní Hermitovy polynomy“ jsou dány vzorcem

{\mathit {He}}_{n}(x)=(-1)^{n}e^{\frac {x^{2}}{2}}{\frac {d^{n}}{{\mbox{d}}x^{n}}}e^{-{\frac {x^{2}}{2}}},

zatímco „fyzikální Hermitovy polynomy“ jsou dány vzorcem

H_{n}(x)=(-1)^{n}e^{x^{2}}{\frac {d^{n}}{{\mbox{d}}x^{n}}}e^{-x^{2}}.

Tyto rovnice mají tvar Rodriguesova vzorce a mohou být také zapsané jako

{\mathit {He}}_{n}(x)=\left(x-{\frac {\mbox{d}}{{\mbox{d}}x}}\right)^{n}\cdot 1,\quad H_{n}(x)=\left(2x-{\frac {\mbox{d}}{{\mbox{d}}x}}\right)^{n}\cdot 1.

Tyto dvě definice nejsou přesně identické; vzájemně se liší použitím jiného měřítka:

H_{n}(x)=2^{\frac {n}{2}}{\mathit {He}}_{n}\left({\sqrt {2}}\,x\right),\quad {\mathit {He}}_{n}(x)=2^{-{\frac {n}{2}}}H_{n}\left({\frac {x}{\sqrt {2}}}\right).

Toto jsou posloupnosti Hermitových polynomů různých variancí; viz výklad o variancích níže.

Notace $He$ a $H$ je, že používán v normě referencí.[5] Polynomy $He n$ jsou někdy označovaný symbolem $H n$ , zvláště v teorie pravděpodobnosti, protože

{\frac {1}{\sqrt {2\pi }}}e^{-{\frac {x^{2}}{2}}}

je hustota pravděpodobnosti pro normální rozdělení se střední hodnotou 0 a směrodatnou odchylkou 1.

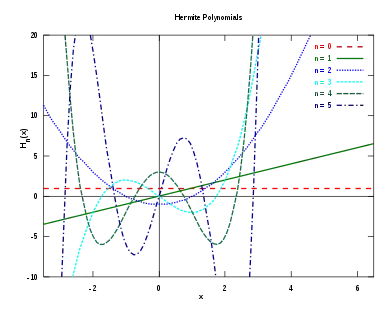
Prvních šest pravděpodobnostních Hermitových polynomů

He n (x)

Prvních jedenáct pravděpodobnostních Hermitových polynomů:

{\begin{aligned}{\mathit {He}}_{0}(x)&=1,\\{\mathit {He}}_{1}(x)&=x,\\{\mathit {He}}_{2}(x)&=x^{2}-1,\\{\mathit {He}}_{3}(x)&=x^{3}-3x,\\{\mathit {He}}_{4}(x)&=x^{4}-6x^{2}+3,\\{\mathit {He}}_{5}(x)&=x^{5}-10x^{3}+15x,\\{\mathit {He}}_{6}(x)&=x^{6}-15x^{4}+45x^{2}-15,\\{\mathit {He}}_{7}(x)&=x^{7}-21x^{5}+105x^{3}-105x,\\{\mathit {He}}_{8}(x)&=x^{8}-28x^{6}+210x^{4}-420x^{2}+105,\\{\mathit {He}}_{9}(x)&=x^{9}-36x^{7}+378x^{5}-1260x^{3}+945x,\\{\mathit {He}}_{10}(x)&=x^{10}-45x^{8}+630x^{6}-3150x^{4}+4725x^{2}-945.\end{aligned}}

Prvních šest (fyzikálních) Hermitových polynomů

H n (x)

Prvních jedenáct fyzikálních Hermitových polynomů:

{\begin{aligned}H_{0}(x)&=1,\\H_{1}(x)&=2x,\\H_{2}(x)&=4x^{2}-2,\\H_{3}(x)&=8x^{3}-12x,\\H_{4}(x)&=16x^{4}-48x^{2}+12,\\H_{5}(x)&=32x^{5}-160x^{3}+120x,\\H_{6}(x)&=64x^{6}-480x^{4}+720x^{2}-120,\\H_{7}(x)&=128x^{7}-1344x^{5}+3360x^{3}-1680x,\\H_{8}(x)&=256x^{8}-3584x^{6}+13440x^{4}-13440x^{2}+1680,\\H_{9}(x)&=512x^{9}-9216x^{7}+48384x^{5}-80640x^{3}+30240x,\\H_{10}(x)&=1024x^{10}-23040x^{8}+161280x^{6}-403200x^{4}+302400x^{2}-30240.\end{aligned}}

Vlastnosti

Hermitův polynom $n$ -tého řádu je polynom stupně $n$ . Pravděpodobnostní verze $He n$ má úvodní koeficient 1, zatímco fyzikální verze $H n$ má úvodní koeficient $2 n$ .

Ortogonalita

$H n (x)$ a $He n (x)$ jsou polynomy $n$ -tého stupně pro $n = 0, 1, 2, 3,...$ . Tyto polynomy jsou ortogonální vzhledem k váhové funkci (míře)

w(x)=e^{-{\frac {x^{2}}{2}}}\quad ({\text{pro }}{\mathit {He}})

nebo

w(x)=e^{-x^{2}}\quad ({\text{pro }}H),

tj. máme

\int _{-\infty }^{\infty }H_{m}(x)H_{n}(x)\,w(x)\,{\mbox{d}}x=0\quad {\text{pro každé }}m\neq n.

Navíc

\int _{-\infty }^{\infty }{\mathit {He}}_{m}(x){\mathit {He}}_{n}(x)\,e^{-{\frac {x^{2}}{2}}}\,{\mbox{d}}x={\sqrt {2\pi }}\,n!\,\delta _{nm},

nebo

\int _{-\infty }^{\infty }H_{m}(x)H_{n}(x)\,e^{-x^{2}}\,{\mbox{d}}x={\sqrt {\pi }}\,2^{n}n!\,\delta _{nm},

kde $\delta _{nm}$ je Kroneckerovo delta.

Pravděpodobnostní polynomy jsou tedy ortogonální vzhledem ke standardní normální hustotě pravděpodobnosti.

Úplnost

Hermitovy polynomy (pravděpodobnostní nebo fyzikální) tvoří ortogonální bázi Hilbertova prostoru funkcí vyhovující

\int _{-\infty }^{\infty }{\bigl |}f(x){\bigr |}^{2}\,w(x)\,{\mbox{d}}x<\infty ,

v který vnitřní součin popisuje vztah integrál

\langle f,g\rangle =\int _{-\infty }^{\infty }f(x){\overline {g(x)}}\,w(x)\,{\mbox{d}}x

včetně Gaussian váhová funkce $w (x)$ definovaný v předchozí část

Ortogonální báze pro $L 2 (R, w (x) d x)$ je úplný ortogonální systém. Pro ortogonální systém je úplnost ekvivalentní se skutečností, že nulová funkce je jediná funkce $f \in L 2 (R, w (x) d x)$ ortogonální se všemi funkcemi v systému.

Protože lineárním obalem Hermitových polynomů je prostor všech polynomů, musíme ukázat (ve fyzikálním případě), že pokud $f$ splňuje

\int _{-\infty }^{\infty }f(x)x^{n}e^{-x^{2}}\,{\mbox{d}}x=0

pro každé $n \geq 0$ , pak $f = 0$ .

Jeden z možných způsobů, jak to udělat, je uvědomit si, že celá funkce

F(z)=\int _{-\infty }^{\infty }f(x)e^{zx-x^{2}}\,{\mbox{d}}x=\sum _{n=0}^{\infty }{\frac {z^{n}}{n!}}\int f(x)x^{n}e^{-x^{2}}\,{\mbox{d}}x=0

bude mít nulovou hodnotu identicky. Skutečnost, že pak bude $F (it) = 0$ pro každé reálné $t$ znamená, že Fourierova transformace $f (x) e - x 2$ je 0, tedy $f$ je 0 skoro všude. Varianty výše uvedeného důkazu úplnosti platí i pro jiné váhy s exponenciálním rozpadem.

V Hermitově případě, je také možné dokázat explicitního identitu, která implikuje úplnost (viz část na Completeness relation níže).

Ekvivalentní formulace faktu, že Hermitovy polynomy jsou ortogonální bází pro $L 2 (R, w (x) d x)$ sestává z v vnášení Hermitova funkce (viz níže) a v saying, že Hermitovy funkce jsou ortonormální bází pro $L 2 (R)$ .

Hermitova diferenciální rovnice

Pravděpodobnostní Hermitovy polynomy jsou řešením diferenciální rovnice

\left(e^{-{\frac {1}{2}}x^{2}}u'\right)'+\lambda e^{-{\frac {1}{2}}x^{2}}u=0,

kde $λ$ je konstanta. Imposing okrajová podmínka, že $u$ musí být polynomiálně omezený v nekonečnu, rovnice má řešení pouze, pokud $λ$ je nezáporné celé číslo a řešení je jednoznačně daný $u(x)=C_{1}He_{\lambda }(x)$ , kde $C_{1}$ označuje konstanta.

Přepsáním diferenciální rovnice jako problém vlastních hodnot

L[u]=u''-xu'=-\lambda u,

Hermitovy polynomy $He_{\lambda }(x)$ můžeme chápat jako vlastní funkce diferenciálního operátoru $L[u]$ . Tento problém vlastní hodnoty se nazývá Hermitova rovnice, i když tento termín se také používá pro blízce příbuzné rovnice

u''-2xu'=-2\lambda u.

jejíž řešení je jednoznačně daný v členy fyzikálních Hermitových polynomů ve tvaru $u(x)=C_{1}H_{\lambda }(x)$ , kde $C_{1}$ označuje konstantu, po stanovení okrajové podmínky, že $u$ musí být polynomiálně omezená v nekonečnu.

Obecné řešení výše uvedené diferenciální rovnice druhého řádu je vlastně lineární kombinací obou Hermitových polynomů a konfluentní hypergeometrické funkce prvního druhu. Například pro fyzikální Hermitova rovnice

u''-2xu'+2\lambda u=0,

obecný řešení má tvar

u(x)=C_{1}H_{\lambda }(x)+C_{2}h_{\lambda }(x),

kde $C_{1}$ a $C_{2}$ jsou konstanty, $H_{\lambda }(x)$ jsou fyzikální Hermitovy polynomy (prvního druhu) a $h_{\lambda }(x)$ jsou fyzikální Hermitovy funkce (druhého druhu). Druhý funkce jsou kompaktně reprezentovány jako $h_{\lambda }(x)={}_{1}F_{1}(-{\tfrac {\lambda }{2}};{\tfrac {1}{2}};x^{2})$ kde ${}_{1}F_{1}(a;b;z)$ jsou konfluentní hypergeometrické funkce prvního druhu. Obvyklé Hermitovy polynomy mohou být také vyjádřeny v pojmech konfluentních hypergeometrických funkcí, viz níže.

S obecnějšími okrajovými podmínkami je možné zobecnit Hermitovy polynomy pro získání obecnějších analytických funkcí pro komplexní $λ$ . Explicitní vzorec Hermitových polynomů pomocí křivkových integrálů [6] je také možné.

Rekurentní vztah

Posloupnost pravděpodobnostních Hermitových polynomů také vyhovuje diferenční rovnici

{\mathit {He}}_{n+1}(x)=x{\mathit {He}}_{n}(x)-{\mathit {He}}_{n}'(x).

Jednotlivé koeficienty jsou příbuzný podle následující rekurzivní vzorec:

a_{n+1,k}={\begin{cases}-na_{n-1,k}&k=0,\\a_{n,k-1}-na_{n-1,k}&k>0,\end{cases}}

a $a 0,0 = 1$ , $a 1,0 = 0$ , $a 1,1 = 1$ .

Pro fyzikální polynomy, předpokládá

H_{n}(x)=\sum _{k=0}^{n}a_{n,k}x^{k},

máme

H_{n+1}(x)=2xH_{n}(x)-H_{n}'(x).

Jednotlivé koeficienty jsou příbuzný podle následujícího rekurzivního vzorce:

a_{n+1,k}={\begin{cases}-a_{n,k+1}&k=0,\\2a_{n,k-1}-(k+1)a_{n,k+1}&k>0,\end{cases}}

a $a 0,0 = 1$ , $a 1,0 = 0$ , $a 1,1 = 2$ .

Hermitovy polynomy tvoří Appellova posloupnost, tj. jsou polynom posloupnost vyhovující identity

{\begin{aligned}{\mathit {He}}_{n}'(x)&=n{\mathit {He}}_{n-1}(x),\\H_{n}'(x)&=2nH_{n-1}(x).\end{aligned}}

Ekvivalentně, podle Taylorova rozvoje,

{\begin{aligned}{\mathit {He}}_{n}(x+y)&=\sum _{k=0}^{n}{\binom {n}{k}}x^{n-k}{\mathit {He}}_{k}(y)&&=2^{-{\frac {n}{2}}}\sum _{k=0}^{n}{\binom {n}{k}}{\mathit {He}}_{n-k}\left(x{\sqrt {2}}\right){\mathit {He}}_{k}\left(y{\sqrt {2}}\right),\\H_{n}(x+y)&=\sum _{k=0}^{n}{\binom {n}{k}}H_{k}(x)(2y)^{(n-k)}&&=2^{-{\frac {n}{2}}}\cdot \sum _{k=0}^{n}{\binom {n}{k}}H_{n-k}\left(x{\sqrt {2}}\right)H_{k}\left(y{\sqrt {2}}\right).\end{aligned}}

Tyto identity stínového počtu jsou evidentní a obsažené v Reprezentace diferenciálním operátorem rozebrané níže

{\begin{aligned}{\mathit {He}}_{n}(x)&=e^{-{\frac {D^{2}}{2}}}x^{n},\\H_{n}(x)&=2^{n}e^{-{\frac {D^{2}}{4}}}x^{n}.\end{aligned}}

V důsledku pro $m$ -tou derivaci platí:

{\begin{aligned}{\mathit {He}}_{n}^{(m)}(x)&={\frac {n!}{(n-m)!}}{\mathit {He}}_{n-m}(x)&&=m!{\binom {n}{m}}{\mathit {He}}_{n-m}(x),\\H_{n}^{(m)}(x)&=2^{m}{\frac {n!}{(n-m)!}}H_{n-m}(x)&&=2^{m}m!{\binom {n}{m}}H_{n-m}(x).\end{aligned}}

Odtud plyne, že Hermitovy polynomy také vyhovují diferenční rovnici

{\begin{aligned}{\mathit {He}}_{n+1}(x)&=x{\mathit {He}}_{n}(x)-n{\mathit {He}}_{n-1}(x),\\H_{n+1}(x)&=2xH_{n}(x)-2nH_{n-1}(x).\end{aligned}}

Tyto poslední vztahy, spolu s počátečními polynomy $H 0 (x)$ a $H 1 (x)$ , mohou být v praxi používány pro rychlý výpočet polynomů.

Turánovy nerovnosti jsou

{\mathit {H}}_{n}(x)^{2}-{\mathit {H}}_{n-1}(x){\mathit {H}}_{n+1}(x)=(n-1)!\sum _{i=0}^{n-1}{\frac {2^{n-i}}{i!}}{\mathit {H}}_{i}(x)^{2}>0.

Navíc platí následující multiplikační věta:

{\begin{aligned}H_{n}(\gamma x)&=\sum _{i=0}^{\left\lfloor {\tfrac {n}{2}}\right\rfloor }\gamma ^{n-2i}(\gamma ^{2}-1)^{i}{\binom {n}{2i}}{\frac {(2i)!}{i!}}H_{n-2i}(x),\\{\mathit {He}}_{n}(\gamma x)&=\sum _{i=0}^{\left\lfloor {\tfrac {n}{2}}\right\rfloor }\gamma ^{n-2i}(\gamma ^{2}-1)^{i}{\binom {n}{2i}}{\frac {(2i)!}{i!}}2^{-i}{\mathit {He}}_{n-2i}(x).\end{aligned}}

Explicitní výraz

Fyzikální Hermitovy polynomy je možné psát explicitně jako

H_{n}(x)={\begin{cases}\displaystyle n!\sum _{l=0}^{\frac {n}{2}}{\frac {(-1)^{{\tfrac {n}{2}}-l}}{(2l)!\left({\tfrac {n}{2}}-l\right)!}}(2x)^{2l}&{\text{pro sudé }}n,\\\displaystyle n!\sum _{l=0}^{\frac {n-1}{2}}{\frac {(-1)^{{\frac {n-1}{2}}-l}}{(2l+1)!\left({\frac {n-1}{2}}-l\right)!}}(2x)^{2l+1}&{\text{pro liché }}n.\end{cases}}

Tyto dvě rovnice je možné zkombinovat do jedné pomocí funkce celá část:

H_{n}(x)=n!\sum _{m=0}^{\left\lfloor {\tfrac {n}{2}}\right\rfloor }{\frac {(-1)^{m}}{m!(n-2m)!}}(2x)^{n-2m}.

Pravděpodobnostní Hermitovy polynomy $He$ mají podobné vzorce, které můžeme získat z těchto nahrazením mocniny $2 x$ odpovídající mocninou $\sqrt 2 x$ a znásobením celého součtu výrazem $2 - n ⁄ 2$ :

He_{n}(x)=n!\sum _{m=0}^{\left\lfloor {\tfrac {n}{2}}\right\rfloor }{\frac {(-1)^{m}}{m!(n-2m)!}}{\frac {x^{n-2m}}{2^{m}}}.

Inverzní explicitní výraz

Inverzí výše uvedených explicitních výrazů, tj. výrazů pro jednočleny v členech pravděpodobnostních Hermitových polynomů $He$ jsou

x^{n}=n!\sum _{m=0}^{\left\lfloor {\tfrac {n}{2}}\right\rfloor }{\frac {1}{2^{m}m!(n-2m)!}}He_{n-2m}(x).

Odpovídající výrazy pro fyzikální Hermitovy polynomy $H$ zjistíme přímo správnou změnou měřítka takto:[7]

x^{n}={\frac {n!}{2^{n}}}\sum _{m=0}^{\left\lfloor {\tfrac {n}{2}}\right\rfloor }{\frac {1}{m!(n-2m)!}}H_{n-2m}(x).

Vytvořující funkce

Hermitovy polynomy lze zadat vytvořující funkcí

{\begin{aligned}e^{xt-{\frac {1}{2}}t^{2}}&=\sum _{n=0}^{\infty }{\mathit {He}}_{n}(x){\frac {t^{n}}{n!}},\\e^{2xt-t^{2}}&=\sum _{n=0}^{\infty }H_{n}(x){\frac {t^{n}}{n!}}.\end{aligned}}

Tato rovnost je platná pro všechny komplexní hodnoty $x$ a $t$ a můžeme ji získat zapsáním Taylorova rozvoje v $x$ celé funkce $z \to e - z 2$ (ve fyzikálním případě). Můžeme také odvodit (fyzikální) vytvořující funkce pomocí Cauchyův vzorec zapsat Hermitovy polynomy jako

H_{n}(x)=(-1)^{n}e^{x^{2}}{\frac {{\mbox{d}}^{n}}{{\mbox{d}}x^{n}}}e^{-x^{2}}=(-1)^{n}e^{x^{2}}{\frac {n!}{2\pi i}}\oint _{\gamma }{\frac {e^{-z^{2}}}{(z-x)^{n+1}}}\,dz.

Dosazením do součtu

\sum _{n=0}^{\infty }H_{n}(x){\frac {t^{n}}{n!}},

můžeme vyhodnotit zbývající integrál pomocí počtu reziduí a dospět k požadované vytvořující funkci.

Očekávaná hodnoty

Pokud $X$ je náhodná veličina s normálním rozdělením se standardní odchylkou 1 a očekávanou hodnotou $μ$ , pak

\operatorname {\mathbb {E} } \left[{\mathit {He}}_{n}(X)\right]=\mu ^{n}.

Momenty standardního normálního rozdělení (s očekávanou hodnotou nula) je možné číst přímo z relace pro sudé indexy:

\operatorname {\mathbb {E} } \left[X^{2n}\right]=(-1)^{n}{\mathit {He}}_{2n}(0)=(2n-1)!!,

kde $(2 n - 1)!!$ je dvojitý faktoriál. Pamatujte, že výše uvedený výraz je speciálním případem reprezentace pravděpodobnostních Hermitových polynomů jako momentů:

{\mathit {He}}_{n}(x)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }(x+iy)^{n}e^{-{\frac {y^{2}}{2}}}\,dy.

Asymptotický rozvoj

Asymptoticky pro $n \to \infty$ , lze použít rozvoj[8]

e^{-{\frac {x^{2}}{2}}}\cdot H_{n}(x)\sim {\frac {2^{n}}{\sqrt {\pi }}}\Gamma \left({\frac {n+1}{2}}\right)\cos \left(x{\sqrt {2n}}-{\frac {n\pi }{2}}\right)

Pro určité případy zabývající se širším rozsahem vyhodnocování je nutné zahrnout faktor pro změnu amplitudy:

e^{-{\frac {x^{2}}{2}}}\cdot H_{n}(x)\sim {\frac {2^{n}}{\sqrt {\pi }}}\Gamma \left({\frac {n+1}{2}}\right)\cos \left(x{\sqrt {2n}}-{\frac {n\pi }{2}}\right)\left(1-{\frac {x^{2}}{2n+1}}\right)^{-{\frac {1}{4}}}={\frac {2\Gamma (n)}{\Gamma \left({\frac {n}{2}}\right)}}\cos \left(x{\sqrt {2n}}-{\frac {n\pi }{2}}\right)\left(1-{\frac {x^{2}}{2n+1}}\right)^{-{\frac {1}{4}}},

což lze, pomocí Stirlingova vzorce dále zjednodušit; v limitě na

e^{-{\frac {x^{2}}{2}}}\cdot H_{n}(x)\sim \left({\frac {2n}{e}}\right)^{\frac {n}{2}}{\sqrt {2}}\cos \left(x{\sqrt {2n}}-{\frac {n\pi }{2}}\right)\left(1-{\frac {x^{2}}{2n+1}}\right)^{-{\frac {1}{4}}}.

Toto rozvoj je potřebný pro řešení vlnové funkce kvantového harmonického oscilátoru tak, že souhlasí s klasickou aproximací v limitě principu korespondence.

Lepší aproximaci, která odpovídá za variaci ve frekvenci, popisuje vztah

e^{-{\frac {x^{2}}{2}}}\cdot H_{n}(x)\sim \left({\frac {2n}{e}}\right)^{\frac {n}{2}}{\sqrt {2}}\cos \left(x{\sqrt {2n+1-{\frac {x^{2}}{3}}}}-{\frac {n\pi }{2}}\right)\left(1-{\frac {x^{2}}{2n+1}}\right)^{-{\frac {1}{4}}}.

Jemnější aproximace,[9] která bere v úvahu nestejný odstup kořenů blízko hrany, používá substituci

x={\sqrt {2n+1}}\cos(\varphi ),\quad 0<\varepsilon \leq \varphi \leq \pi -\varepsilon ,

se kterou máme rovnoměrnou aproximaci

e^{-{\frac {x^{2}}{2}}}\cdot H_{n}(x)=2^{{\frac {n}{2}}+{\frac {1}{4}}}{\sqrt {n!}}(\pi n)^{-{\frac {1}{4}}}(\sin \varphi )^{-{\frac {1}{2}}}\cdot \left(\sin \left({\frac {3\pi }{4}}+\left({\frac {n}{2}}+{\frac {1}{4}}\right)\left(\sin 2\varphi -2\varphi \right)\right)+O\left(n^{-1}\right)\right).

Podobná aproximace platí pro monotonní a přechod oblasti. Konkrétně pokud

x={\sqrt {2n+1}}\cosh(\varphi ),\quad 0<\varepsilon \leq \varphi \leq \omega <\infty ,

pak

e^{-{\frac {x^{2}}{2}}}\cdot H_{n}(x)=2^{{\frac {n}{2}}-{\frac {3}{4}}}{\sqrt {n!}}(\pi n)^{-{\frac {1}{4}}}(\sinh \varphi )^{-{\frac {1}{2}}}\cdot e^{\left({\frac {n}{2}}+{\frac {1}{4}}\right)\left(2\varphi -\sinh 2\varphi \right)}\left(1+O\left(n^{-1}\right)\right),

zatímco pro

x={\sqrt {2n+1}}+t

s $t$ složitý a omezený, aproximace je

e^{-{\frac {x^{2}}{2}}}\cdot H_{n}(x)=\pi ^{\frac {1}{4}}2^{{\frac {n}{2}}+{\frac {1}{4}}}{\sqrt {n!}}\,n^{-{\frac {1}{12}}}\left(\operatorname {Ai} \left(2^{\frac {1}{2}}n^{\frac {1}{6}}t\right)+O\left(n^{-{\frac {2}{3}}}\right)\right),

kde $Ai$ je Airyho funkce prvního druhu.

Speciální hodnoty

Fyzikální Hermitovy polynomy vyčíslené v bodě nula $H n (0)$ se nazývají Hermitova čísla.

H_{n}(0)={\begin{cases}0&{\text{pro lichá }}n,\\(-2)^{\frac {n}{2}}(n-1)!!&{\text{pro sudé }}n,\end{cases}}

což vyhovuje rekurzivní relaci $H n (0) = -2(n - 1) H n - 2 (0)$ .

V členech pravděpodobnostních polynomů se převádí na

He_{n}(0)={\begin{cases}0&{\text{pro liché }}n,\\(-1)^{\frac {n}{2}}(n-1)!!&{\text{pro sudé }}n.\end{cases}}

Vztahy k jiný funkce

Laguerrovy polynomy

Hermitovy polynomy může být vyjádřený jako speciální případ Laguerrových polynomů:

{\begin{aligned}H_{2n}(x)&=(-4)^{n}n!L_{n}^{\left(-{\frac {1}{2}}\right)}(x^{2})&&=4^{n}n!\sum _{k=0}^{n}(-1)^{n-k}{\binom {n-{\frac {1}{2}}}{n-k}}{\frac {x^{2k}}{k!}},\\H_{2n+1}(x)&=2(-4)^{n}n!xL_{n}^{\left({\frac {1}{2}}\right)}(x^{2})&&=2\cdot 4^{n}n!\sum _{k=0}^{n}(-1)^{n-k}{\binom {n+{\frac {1}{2}}}{n-k}}{\frac {x^{2k+1}}{k!}}.\end{aligned}}

Vztah k konfluentním hypergeometrickým funkcím

Fyzikální Hermitovy polynomy je možné vyjádřit jako speciální případ parabolických válcových funkcí:

H_{n}(x)=2^{n}U\left(-{\tfrac {1}{2}}n,{\tfrac {1}{2}},x^{2}\right)

v pravé polorovině, kde $U (a, b, z)$ je Tricomiho konfluentní hypergeometrické funkce. Podobně

{\begin{aligned}H_{2n}(x)&=(-1)^{n}{\frac {(2n)!}{n!}}\,_{1}F_{1}{\big (}-n,{\tfrac {1}{2}};x^{2}{\big )},\\H_{2n+1}(x)&=(-1)^{n}{\frac {(2n+1)!}{n!}}\,2x\,_{1}F_{1}{\big (}-n,{\tfrac {3}{2}};x^{2}{\big )},\end{aligned}}

kde $1 F 1 (a, b; z) = M (a, b; z)$ je Kummerova konfluentní hypergeometrické funkce.

Reprezentace diferenciálním operátorem

Pravděpodobnostní Hermitovy polynomy vyhovují vztahu

{\mathit {He}}_{n}(x)=e^{-{\frac {D^{2}}{2}}}x^{n},

kde $D$ reprezentuje rozlišení vzhledem k $x$ a exponenciální je interpretovány jejím rozvojem jako Mocninná řada. Neexistuje delicate otázky konvergence tohoto řada, když ono funguje na polynomy, protože všechny členy kromě konečně mnoha členů zanikají.

Protože koeficienty mocninné řady exponenciální funkce jsou dobře známé a derivace vyššího řádu jednočlenu $x n$ je možné zapsat explicitně, tato reprezentace diferenciálním operátorem dává konkrétní vzorec pro koeficienty $H n$ , který lze použít pro rychlý výpočet těchto polynomů.

Protože formální výraz pro Weierstrassovu transformaci $W$ je $e D 2$ , vidíme, že Weierstrassova transformace $(\sqrt 2) n He n (x ⁄ \sqrt 2)$ je $x n$ . Weierstrassova transformace tedy v zásadě převede řadu Hermitových polynomů na odpovídající Taylorovu řadu.

Existence nějaké formální mocninné řady $g (D)$ s nenulovým konstantním koeficientem, tak, že $He n (x) = g (D) x n$ , je dalším ekvivalentem tvrzení, že tyto polynomy tvoří Appellovu posloupnost. Protože jsou Appellovou posloupností, jsou a fortiori Shefferovou posloupností.

Reprezentace křivkovým integrálem

Z reprezentace generující funkce uvedené výše, vidíme, že Hermitovy polynomy lze reprezentovat pomocí křivkový integrál, protože

{\begin{aligned}{\mathit {He}}_{n}(x)&={\frac {n!}{2\pi i}}\oint _{C}{\frac {e^{tx-{\frac {t^{2}}{2}}}}{t^{n+1}}}\,dt,\\H_{n}(x)&={\frac {n!}{2\pi i}}\oint _{C}{\frac {e^{2tx-t^{2}}}{t^{n+1}}}\,dt,\end{aligned}}

s křivkou obkružující počátek souřadnicového systému.

Zobecnění

Pravděpodobnostní Hermitovy polynomy definované výše jsou ortogonální vůči standardnímu normálnímu rozdělení pravděpodobnosti, jehož hustota je

{\frac {1}{\sqrt {2\pi }}}e^{-{\frac {x^{2}}{2}}},

a které má očekávanou hodnotu 0 a rozptyl 1.

Při změně měřítka můžeme obdobně mluvit o zobecněných Hermitových polynomech[10]

{\mathit {He}}_{n}^{[\alpha ]}(x)

s rozptylem $α$ , kde $α$ je jakékoli kladné číslo. Tyto jsou pak ortogonální vzhledem k normální rozdělení pravděpodobnosti, jejíž hustota je

(2\pi \alpha )^{-{\frac {1}{2}}}e^{-{\frac {x^{2}}{2\alpha }}}.

Jsou daný

{\mathit {He}}_{n}^{[\alpha ]}(x)=\alpha ^{\frac {n}{2}}{\mathit {He}}_{n}\left({\frac {x}{\sqrt {\alpha }}}\right)=\left({\frac {\alpha }{2}}\right)^{\frac {n}{2}}H_{n}\left({\frac {x}{\sqrt {2\alpha }}}\right)=e^{-{\frac {\alpha D^{2}}{2}}}\left(x^{n}\right).

Nyní, pokud

{\mathit {He}}_{n}^{[\alpha ]}(x)=\sum _{k=0}^{n}h_{n,k}^{[\alpha ]}x^{k},

pak polynom posloupnost, jejíž $n$ -tý člen je

\left({\mathit {He}}_{n}^{[\alpha ]}\circ {\mathit {He}}^{[\beta ]}\right)(x)\equiv \sum _{k=0}^{n}h_{n,k}^{[\alpha ]}\,{\mathit {He}}_{k}^{[\beta ]}(x)

se nazývá stínová kompozice ze dvou posloupností polynomů. Je možné ukázat, že vyhovuje identitám

\left({\mathit {He}}_{n}^{[\alpha ]}\circ {\mathit {He}}^{[\beta ]}\right)(x)={\mathit {He}}_{n}^{[\alpha +\beta ]}(x)

a

{\mathit {He}}_{n}^{[\alpha +\beta ]}(x+y)=\sum _{k=0}^{n}{\binom {n}{k}}{\mathit {He}}_{k}^{[\alpha ]}(x){\mathit {He}}_{n-k}^{[\beta ]}(y).

Poslední vztah lze vyjádřit tím, že řekneme, že tato parametrizovaná rodina posloupností polynomů je známá jako křížová posloupnost. (Viz výše uvedená část o Appellových posloupnostech a o reprezentaci diferenciálním operátorem, která vede k její připravené derivaci. Tato vztah identity binomického typu pro $α = β = 1 ⁄ 2$ jsme již zaznamenali ve výše uvedené části o Rekurentních vztazích.)

„Záporný rozptyl“

Protože posloupnosti polynomů tvoří grupu s operací stínová kompozice, můžeme pomocí

{\mathit {He}}_{n}^{[-\alpha ]}(x)

zapsat posloupnost, která je inverzní k podobně označené posloupnosti, ale bez znaménka minus, proto mluvíme o Hermitových polynomech se záporným rozptylem. Pro $α > 0$ koeficienty ${\mathit {He}}_{n}^{[-\alpha ]}(x)$ jsou pouze absolutními hodnotami odpovídajících koeficientů ${\mathit {He}}_{n}^{[\alpha ]}(x)$ .

Tyto se objevují jako momenty normálního rozdělení pravděpodobnosti: $n$ -tý moment normálního rozdělení s očekávanou hodnotou $μ$ a rozptylem $σ 2$ je

E[X^{n}]={\mathit {He}}_{n}^{[-\sigma ^{2}]}(\mu ),

kde $X$ je náhodná proměnná se zadaným normálním rozdělením. Speciální případ křížové posloupnosti identit pak říká, že

\sum _{k=0}^{n}{\binom {n}{k}}{\mathit {He}}_{k}^{[\alpha ]}(x){\mathit {He}}_{n-k}^{[-\alpha ]}(y)={\mathit {He}}_{n}^{[0]}(x+y)=(x+y)^{n}.

Aplikace

Hermitovy funkce

Můžeme definovat Hermitovy funkce (často nazývané Hermitovy-gaussovské funkce) z fyzikálních polynomů:

\psi _{n}(x)=\left(2^{n}n!{\sqrt {\pi }}\right)^{-{\frac {1}{2}}}e^{-{\frac {x^{2}}{2}}}H_{n}(x)=(-1)^{n}\left(2^{n}n!{\sqrt {\pi }}\right)^{-{\frac {1}{2}}}e^{\frac {x^{2}}{2}}{\frac {d^{n}}{{\mbox{d}}x^{n}}}e^{-x^{2}}.

Tedy

{\sqrt {2(n+1)}}~~\psi _{n+1}(x)=\left(x-{d \over {\mbox{d}}x}\right)\psi _{n}(x).

Protože tyto funkce obsahují druhou odmocnina váhové funkce a jejich měřítko bylo vhodným způsobem upravené, jsou ortonormální:

\int _{-\infty }^{\infty }\psi _{n}(x)\psi _{m}(x)\,{\mbox{d}}x=\delta _{nm},

a tvoří ortonormální bázi $L 2 (R)$ . Tato skutečnost je ekvivalentní s odpovídajícím tvrzení pro Hermitovy polynomy (viz výše).

Hermitovy funkce úzce souvisí s Whittakerovou funkcí [11] $D n (z)$ :

D_{n}(z)=\left(n!{\sqrt {\pi }}\right)^{\frac {1}{2}}\psi _{n}\left({\frac {z}{\sqrt {2}}}\right)=(-1)^{n}e^{\frac {z^{2}}{4}}{\frac {d^{n}}{dz^{n}}}e^{\frac {-z^{2}}{2}}

a díky tomu i s další parabolickou válcovou funkcí.

Hermitovy funkce vyhovují diferenciální rovnici

\psi _{n}''(x)+\left(2n+1-x^{2}\right)\psi _{n}(x)=0.

Tato rovnice je ekvivalentní s Schrödingerovou rovnicí pro harmonický oscilátor v kvantové mechanice, takže tyto funkce jsou vlastní funkce.

Hermitova funkce: 0 (plná modrá), 1 (čárkovaná oranžová), 2 (tečkovaná zelená), 3 (tečkovaná červená), 4 (plná fialová), a 5 (čárkovaná hnědá)

{\begin{aligned}\psi _{0}(x)&=\pi ^{-{\frac {1}{4}}}\,e^{-{\frac {1}{2}}x^{2}},\\\psi _{1}(x)&={\sqrt {2}}\,\pi ^{-{\frac {1}{4}}}\,x\,e^{-{\frac {1}{2}}x^{2}},\\\psi _{2}(x)&=\left({\sqrt {2}}\,\pi ^{\frac {1}{4}}\right)^{-1}\,\left(2x^{2}-1\right)\,e^{-{\frac {1}{2}}x^{2}},\\\psi _{3}(x)&=\left({\sqrt {3}}\,\pi ^{\frac {1}{4}}\right)^{-1}\,\left(2x^{3}-3x\right)\,e^{-{\frac {1}{2}}x^{2}},\\\psi _{4}(x)&=\left(2{\sqrt {6}}\,\pi ^{\frac {1}{4}}\right)^{-1}\,\left(4x^{4}-12x^{2}+3\right)\,e^{-{\frac {1}{2}}x^{2}},\\\psi _{5}(x)&=\left(2{\sqrt {15}}\,\pi ^{\frac {1}{4}}\right)^{-1}\,\left(4x^{5}-20x^{3}+15x\right)\,e^{-{\frac {1}{2}}x^{2}}.\end{aligned}}

Hermitova funkce: 0 (plná modrá), 1 (čárkovaná oranžová), 2 (tečkovaná zelená), 3 (tečkovaná červená), 4 (plná fialová) a 5 (čárkovaná hnědá)

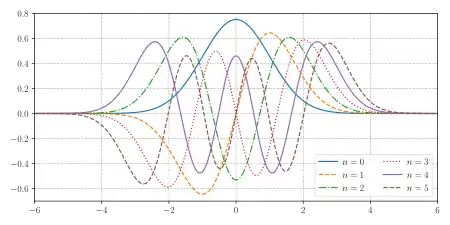
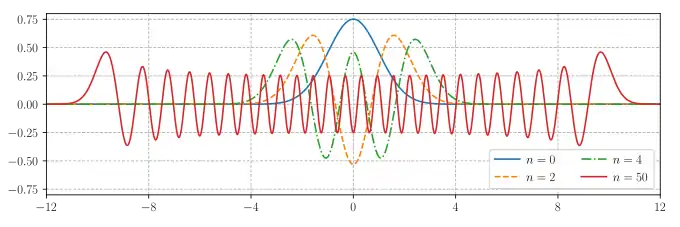
Rekurzivní relace

Díky rekurzivní relaci Hermitových polynomů zachovávají Hermitovy funkce

\psi _{n}'(x)={\sqrt {\frac {n}{2}}}\,\psi _{n-1}(x)-{\sqrt {\frac {n+1}{2}}}\psi _{n+1}(x)

a

x\psi _{n}(x)={\sqrt {\frac {n}{2}}}\,\psi _{n-1}(x)+{\sqrt {\frac {n+1}{2}}}\psi _{n+1}(x).

Rozvoj prvního vztahu pro libovolnou $m$ -tou derivaci pro jakékoli kladné celé číslo $m$ vede k

\psi _{n}^{(m)}(x)=\sum _{k=0}^{m}{\binom {m}{k}}(-1)^{k}2^{\frac {m-k}{2}}{\sqrt {\frac {n!}{(n-m+k)!}}}\psi _{n-m+k}(x){\mathit {He}}_{k}(x).

Tento vzorec může být používán ve spojení s rekurentními vztahy pro $He n$ a $ψ n$ pro efektivní výpočet jakékoli derivace Hermitovy funkce.

Cramérova nerovnost

Pro reálné $x$ vyhovují Hermitovy funkce následujícímu omezení, které ukázali Harald Cramér[12][13] a Jack Indritz:[14]

{\bigl |}\psi _{n}(x){\bigr |}\leq \pi ^{-{\frac {1}{4}}}.

Hermitovy funkce jako vlastní funkce Fourierovy transformace

Hermitovy funkce $ψ n (x)$ jsou sadou vlastních funkcí Fourierovy transformace ${\mathcal {F}}$ . Pro zjištění toto, použijeme fyzikální verzi vytvořující funkce a znásobíme ji $e - 1 ⁄ 2 x 2$ . Tím dostaneme

e^{-{\frac {1}{2}}x^{2}+2xt-t^{2}}=\sum _{n=0}^{\infty }e^{-{\frac {1}{2}}x^{2}}H_{n}(x){\frac {t^{n}}{n!}}.

Fourierova transformace levé strany popisuje vztah

{\begin{aligned}{\mathcal {F}}\left\{e^{-{\frac {1}{2}}x^{2}+2xt-t^{2}}\right\}(k)&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }e^{-ixk}e^{-{\frac {1}{2}}x^{2}+2xt-t^{2}}\,{\mbox{d}}x\\&=e^{-{\frac {1}{2}}k^{2}-2kit+t^{2}}\\&=\sum _{n=0}^{\infty }e^{-{\frac {1}{2}}k^{2}}H_{n}(k){\frac {(-it)^{n}}{n!}}.\end{aligned}}

Fourierova transformace pravé strany popisuje vztah

{\mathcal {F}}\left\{\sum _{n=0}^{\infty }e^{-{\frac {1}{2}}x^{2}}H_{n}(x){\frac {t^{n}}{n!}}\right\}=\sum _{n=0}^{\infty }{\mathcal {F}}\left\{e^{-{\frac {1}{2}}x^{2}}H_{n}(x)\right\}{\frac {t^{n}}{n!}}.

Srovnáním stejných mocnin $t$ v transformované verzi levé a pravé strany nakonec dává

{\mathcal {F}}\left\{e^{-{\frac {1}{2}}x^{2}}H_{n}(x)\right\}=(-i)^{n}e^{-{\frac {1}{2}}k^{2}}H_{n}(k).

Hermitovy funkce $ψ n (x)$ jsou tedy ortonormální bází $L 2 (R)$ , což diagonalizuje Fourierův transformační operátor.[15]

Wignerova distribuce Hermitovy funkce

Wignerova distribuční funkce $n$ -tého řádu Hermitova funkce souvisí s Laguerrovými polynomy $n$ -tého řádu. Laguerrovy polynomy jsou

L_{n}(x):=\sum _{k=0}^{n}{\binom {n}{k}}{\frac {(-1)^{k}}{k!}}x^{k},

což vede k oscilátorovým Laguerrovým funkcím

l_{n}(x):=e^{-{\frac {x}{2}}}L_{n}(x).

Pro všechna přirozená celá čísla $n$ , je přímočaré vidět,[16] že

W_{\psi _{n}}(t,f)=(-1)^{n}l_{n}{\big (}4\pi (t^{2}+f^{2}){\big )},

kde Wignerova funkce rozdělení $x \in L 2 (R, C)$ je definována jako

W_{x}(t,f)=\int _{-\infty }^{\infty }x\left(t+{\frac {\tau }{2}}\right)\,x\left(t-{\frac {\tau }{2}}\right)^{*}\,e^{-2\pi i\tau f}\,d\tau .

To je základní výsledek pro kvantový harmonický oscilátor, který objevil Hilbrand J. Groenewold v roce 1946 a publikoval ve své disertační práci.[17] Jedná se o standardní paradigma kvantové mechaniky ve fázovém prostoru.

Mezi těmito dvěma rodinami polynomů existují další vztahy.

Kombinatorická interpretace koeficientů

V Hermitově polynomu $He n (x)$ s rozptylem 1 je absolutní hodnota koeficientu $x k$ rovna počtu (neuspořádaných) dělení $n$ -prvkové množiny na $k$ singletonů a $n - k ⁄ 2$ (neuspořádaných) dvojic. Ekvivalentně je to počet involucí $n$ -prvkové množiny s právě $k$ pevnými body nebo jinými slovy počet párování v úplném grafu s $n$ vrcholy, která ponechávají $k$ vrcholů nepokrytých (skutečně, Hermitovy polynomy jsou polynomy párování těchto grafů). Součet absolutních hodnot koeficientů dává celkový počet dělení na singletony a dvojice, tak zvaná telefonní čísla

1, 1, 2, 4, 10, 26, 76, 232, 764, 2620, 9496,... Posloupnost A000085 v databázi On-Line Encyclopedia of Integer Sequences.

Tato kombinatorická interpretace je příbuzná s kompletními exponenciálními Bellovými polynomy jako

{\mathit {He}}_{n}(x)=B_{n}(x,-1,0,\ldots ,0),

kde $x i = 0$ pro všechna $i > 2$ .

Tato čísla je možné také vyjádřit jako speciální hodnotu Hermitových polynomů:[18]

T(n)={\frac {{\mathit {He}}_{n}(i)}{i^{n}}}.

Vztah úplnosti

Christoffelův–Darbouxův vzorec pro Hermitovy polynomy má tvar

\sum _{k=0}^{n}{\frac {H_{k}(x)H_{k}(y)}{k!2^{k}}}={\frac {1}{n!2^{n+1}}}\,{\frac {H_{n}(y)H_{n+1}(x)-H_{n}(x)H_{n+1}(y)}{x-y}}.

Navíc následující identita úplnosti pro výše uvedené Hermitovy funkce platí ve smyslu distribucí:

\sum _{n=0}^{\infty }\psi _{n}(x)\psi _{n}(y)=\delta (x-y),

kde $δ$ je Diracovo delta, $ψ n$ Hermitovy funkce a $δ (x - y)$ reprezentuje Lebesgueovu míru na přímce $y = x$ v $R 2$ normalizovanou tak, že její projekce na horizontální osu je obvyklá Lebesgueova míra.

Tato distribuční identita podle [19] vyplývá z použití limity $u \to 1$ v Mehlerově vzorci, který je platný pro $-1 < u < 1$ :

E(x,y;u):=\sum _{n=0}^{\infty }u^{n}\,\psi _{n}(x)\,\psi _{n}(y)={\frac {1}{\sqrt {\pi (1-u^{2})}}}\,\exp \left(-{\frac {1-u}{1+u}}\,{\frac {(x+y)^{2}}{4}}-{\frac {1+u}{1-u}}\,{\frac {(x-y)^{2}}{4}}\right),

což se často uvádí ekvivalentně jako separabilní jádro,[20][21]

\sum _{n=0}^{\infty }{\frac {H_{n}(x)H_{n}(y)}{n!}}\left({\frac {u}{2}}\right)^{n}={\frac {1}{\sqrt {1-u^{2}}}}e^{{\frac {2u}{1+u}}xy-{\frac {u^{2}}{1-u^{2}}}(x-y)^{2}}.

Funkce $(x, y) \to E (x, y; u)$ je gaussovská pravděpodobnostní hustota funkce dvou proměnných na $R 2$ , která je při přiblížení $u$ k 1, velmi zahuštěná kolem přímky $y = x$ a velmi roztažená dále od této přímky. Odtud plyne, že

\sum _{n=0}^{\infty }u^{n}\langle f,\psi _{n}\rangle \langle \psi _{n},g\rangle =\iint E(x,y;u)f(x){\overline {g(y)}}\,{\mbox{d}}x\,{\mbox{d}}y\to \int f(x){\overline {g(x)}}\,{\mbox{d}}x=\langle f,g\rangle

když $f$ a $g$ jsou spojité a mají kompaktní support.

Odtud je možné vyjádřit $f$ v Hermitově funkci jako sumu řady vektorů v $L 2 (R)$ , jmenovitě,

f=\sum _{n=0}^{\infty }\langle f,\psi _{n}\rangle \psi _{n}.

Pro důkaz této rovnosti pro $E (x, y; u)$ použijeme opakovaně Fourierovu transformaci Gaussových funkcí:

\rho {\sqrt {\pi }}e^{-{\frac {\rho ^{2}x^{2}}{4}}}=\int e^{isx-{\frac {s^{2}}{\rho ^{2}}}}\,ds\quad {\text{for }}\rho >0.

Hermitův polynom je pak reprezentován jako

H_{n}(x)=(-1)^{n}e^{x^{2}}{\frac {{\mbox{d}}^{n}}{{\mbox{d}}x^{n}}}\left({\frac {1}{2{\sqrt {\pi }}}}\int e^{isx-{\frac {s^{2}}{4}}}\,ds\right)=(-1)^{n}e^{x^{2}}{\frac {1}{2{\sqrt {\pi }}}}\int (is)^{n}e^{isx-{\frac {s^{2}}{4}}}\,ds.

S touto reprezentací $H n (x)$ a $H n (y)$ je zřejmé, že

{\begin{aligned}E(x,y;u)&=\sum _{n=0}^{\infty }{\frac {u^{n}}{2^{n}n!{\sqrt {\pi }}}}\,H_{n}(x)H_{n}(y)e^{-{\frac {x^{2}+y^{2}}{2}}}\\&={\frac {e^{\frac {x^{2}+y^{2}}{2}}}{4\pi {\sqrt {\pi }}}}\iint \left(\sum _{n=0}^{\infty }{\frac {1}{2^{n}n!}}(-ust)^{n}\right)e^{isx+ity-{\frac {s^{2}}{4}}-{\frac {t^{2}}{4}}}\,ds\,dt\\&={\frac {e^{\frac {x^{2}+y^{2}}{2}}}{4\pi {\sqrt {\pi }}}}\iint e^{-{\frac {ust}{2}}}\,e^{isx+ity-{\frac {s^{2}}{4}}-{\frac {t^{2}}{4}}}\,ds\,dt,\end{aligned}}

což dává požadované rozlišení identity výsledku, opět pomocí Fourierovy transformace gaussovských jader při substituci

s={\frac {\sigma +\tau }{\sqrt {2}}},\quad t={\frac {\sigma -\tau }{\sqrt {2}}}.

Odkazy

Poznámky

Laplace 1810 (online).
LAPLACE, P.-S. Théorie analytique des probabilités. [s.l.]: [s.n.], 1812. S. 194–203. Collected v Œuvres complètes VII.
CHEBYSHEV, P. L. Sur le développement des fonctions à une seule variable. Bull. Acad. Sci. St. Petersb.. 1859, roč. 1, s. 193–200. Collected v Œuvres I, 501–508.
HERMITE, C. Sur un nouveau développement en série de fonctions. C. R. Acad. Sci. Paris. 1864, roč. 58, s. 93–100. Collected v Œuvres II, 293–303.
Koornwinder et al. 2010 a Abramowitz & Stegun.
Courant a Hilbert 1989.
18. Orthogonal Polynomials, Classical Orthogonal Polynomials, Sums [online]. National Institute of Standards and Technology [cit. 2015-01-30]. Dostupné online.
Abramowitz & Stegun 1983, 13.6.38 a 13.5.16.
Szegő 1955, s. 201.
ROMAN, Steven. The Umbral Calculus. 1. vyd. [s.l.]: Academic Press, 1984. (Pure and Applied Mathematics). ISBN 978-0-12-594380-2. S. 87–93.
Whittaker a Watson 1996.
Erdélyi et al. 1955.
Szegő 1955.
INDRITZ, Jack, 1961. An inequality for Hermite polynomials. Proceedings of the American Mathematical Society. Roč. 12, čís. 6, s. 981–983. DOI 10.1090/S0002-9939-1961-0132852-2.
V tomto případě jsme použili unitární verzi Fourierovy transformace, takže vlastní čísla jsou $(- i) n$ . Následující rozlišení identity pak slouží k definici mocnin Fourierovy transformace (včetně racionálních) pro rychlé získání zobecnění zlomkové Fourierovy transformace, ve výsledku Mehlerova jádra.
FOLLAND, G. B. Harmonic Analysis in Phase Space. [s.l.]: Princeton University Press, 1989. (Annals of Mathematics Studies). ISBN 978-0-691-08528-9.
GROENEWOLD, H. J., 1946. On the Principles of elementary quantum mechanics. Physica. Roč. 12, čís. 7, s. 405–460. DOI 10.1016/S0031-8914(46)80059-4. Bibcode 1946Phy....12..405G.
BANDERIER, Cyril; BOUSQUET-MÉLOU, Mireille; DENISE, Alain; FLAJOLET, Philippe; GARDY, Danièle; GOUYOU-BEAUCHAMPS, Dominique, 2002. Generating functions for generating trees. Discrete Mathematics. Roč. 246, čís. 1–3, s. 29–55. DOI 10.1016/S0012-365X(01)00250-3. arXiv math/0411250.
Wiener 1958.
MEHLER, F. G., 1866. Ueber die Entwicklung einer Function von beliebig vielen Variabeln nach Laplaceschen Functionen höherer Ordnung. Journal für die Reine und Angewandte Mathematik. Čís. 66, s. 161–176. Dostupné online. ISSN 0075-4102. Šablona:ERAM. (německy). Viz p. 174, eq. (18) a p. 173, eq. (13).
Erdélyi et al. 1955, 10.13 (22).

Reference

V tomto článku byl použit překlad textu z článku Hermite polynomials na anglické Wikipedii.

Je zde použita šablona {{Refbegin}} označená jako k „pouze dočasnému použití“.

Literatura

ABRAMOWITZ, Milton; STEGUN, Irena Ann, 1972. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. 9. vyd. Washington D.C.; New York: Dover. ISBN 978-0-486-61272-0. Kapitola 22.
COURANT, Richard; HILBERT, David, 1989. Methods of Mathematical Physics. [s.l.]: Wiley-Interscience. ISBN 978-0-471-50447-4.
ERDÉLYI, Arthur; MAGNUS, Wilhelm; OBERHETTINGER, Fritz; TRICOMI, Francesco G., 1955. Higher transcendental functions. [s.l.]: McGraw-Hill. Dostupné online. ISBN 978-0-07-019546-2.
FEDORYUK, M.V. Hermite function. [s.l.]: EMS Press, 2001.
KOORNWINDER, Tom H.; WONG, Roderick S. C.; KOEKOEK, Roelof; SWARTTOUW, René F. Orthogonal Polynomials. Příprava vydání Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W.. [s.l.]: Cambridge University Press ISBN 978-0-521-19225-5. p/o070340.
LAPLACE, P. S., 1810. Mémoire sur les intégrales déﬁnies et leur application aux probabilités, et spécialement a la recherche du milieu qu'il faut choisir entre les résultats des observations. Mémoires de l'Académie des Sciences. S. 279–347. Oeuvres complètes 12, pp.357-412, anglický překlad/translace Archivováno 4. 3. 2016 na Wayback Machine.
SHOHAT, J.A.; HILLE, Einar; WALSH, Joseph L. A bibliography on orthogonal polynomials. Washington D.C.: National Academy of Sciences, 1940. (Bulletin of the National Research Council). - 2000 referencí of Bibliography na Hermitovy polynomy.
SUETIN, P. K. Hermite polynomials. [s.l.]: EMS Press, 2001.
SZEGŐ, Gábor, 1955. Orthogonal Polynomials. 4. vyd. [s.l.]: American Mathematical Society. (Colloquium Publications). ISBN 978-0-8218-1023-1.
TEMME, Nico. Special Functions: An Introduction to the Classical Functions of Mathematical Physics. New York: Wiley, 1996. ISBN 978-0-471-11313-3.
WIENER, Norbert, 1958. The Fourier Integral and Certain of its Applications. revised. vyd. New York: Dover Publications. Dostupné online. ISBN 0-486-60272-9.
WHITTAKER, E. T.; WATSON, G. N., 1996. A Course of Modern Analysis. 4. vyd. London: Cambridge University Press. ISBN 978-0-521-58807-2.

Související články

Hermitova transformace
Legendreovy polynomy
Mehlerovo jádro
Parabolická válcová funkce
Romanovského polynomy
Turánovy nerovnosti

Externí odkazy

Hermitovy polynomy v encyklopedii MathWorld (anglicky)
GNU Scientific Library — knihovna pro jazyk C implementující Hermitovy polynomy, funkce, jejich derivace a kořeny (viz také GNU Scientific Library)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Laplace 1810 (online).

[2] LAPLACE, P.-S. Théorie analytique des probabilités. [s.l.]: [s.n.], 1812. S. 194–203. Collected v Œuvres complètes VII.

[3] CHEBYSHEV, P. L. Sur le développement des fonctions à une seule variable. Bull. Acad. Sci. St. Petersb.. 1859, roč. 1, s. 193–200. Collected v Œuvres I, 501–508.

[4] HERMITE, C. Sur un nouveau développement en série de fonctions. C. R. Acad. Sci. Paris. 1864, roč. 58, s. 93–100. Collected v Œuvres II, 293–303.

[5] Koornwinder et al. 2010 a Abramowitz & Stegun.

[FOOTNOTECourantHilbert1989-6] Courant a Hilbert 1989.

[7] 18. Orthogonal Polynomials, Classical Orthogonal Polynomials, Sums [online]. National Institute of Standards and Technology [cit. 2015-01-30]. Dostupné online.

[8] Abramowitz & Stegun 1983, 13.6.38 a 13.5.16.

[FOOTNOTESzegő1955201-9] Szegő 1955, s. 201.

[10] ROMAN, Steven. The Umbral Calculus. 1. vyd. [s.l.]: Academic Press, 1984. (Pure and Applied Mathematics). ISBN 978-0-12-594380-2. S. 87–93.

[FOOTNOTEWhittakerWatson1996-11] Whittaker a Watson 1996.

[12] Erdélyi et al. 1955.

[13] Szegő 1955.

[indritz-14] INDRITZ, Jack, 1961. An inequality for Hermite polynomials. Proceedings of the American Mathematical Society. Roč. 12, čís. 6, s. 981–983. DOI 10.1090/S0002-9939-1961-0132852-2.

[15] V tomto případě jsme použili unitární verzi Fourierovy transformace, takže vlastní čísla jsou $(- i) n$ . Následující rozlišení identity pak slouží k definici mocnin Fourierovy transformace (včetně racionálních) pro rychlé získání zobecnění zlomkové Fourierovy transformace, ve výsledku Mehlerova jádra.

[16] FOLLAND, G. B. Harmonic Analysis in Phase Space. [s.l.]: Princeton University Press, 1989. (Annals of Mathematics Studies). ISBN 978-0-691-08528-9.

[Groenewold1946-17] GROENEWOLD, H. J., 1946. On the Principles of elementary quantum mechanics. Physica. Roč. 12, čís. 7, s. 405–460. DOI 10.1016/S0031-8914(46)80059-4. Bibcode 1946Phy....12..405G.

[gfgt-18] BANDERIER, Cyril; BOUSQUET-MÉLOU, Mireille; DENISE, Alain; FLAJOLET, Philippe; GARDY, Danièle; GOUYOU-BEAUCHAMPS, Dominique, 2002. Generating functions for generating trees. Discrete Mathematics. Roč. 246, čís. 1–3, s. 29–55. DOI 10.1016/S0012-365X(01)00250-3. arXiv math/0411250.

[FOOTNOTEWiener1958-19] Wiener 1958.

[20] MEHLER, F. G., 1866. Ueber die Entwicklung einer Function von beliebig vielen Variabeln nach Laplaceschen Functionen höherer Ordnung. Journal für die Reine und Angewandte Mathematik. Čís. 66, s. 161–176. Dostupné online. ISSN 0075-4102. Šablona:ERAM. (německy). Viz p. 174, eq. (18) a p. 173, eq. (13).

[21] Erdélyi et al. 1955, 10.13 (22).