Křivkový integrál
V matematice je křivkový integrál integrál skalárního nebo vektorového pole počítaný podél křivky. Je mnoho druhů křivkových integrálů, mezi nejdůležitější patří integrály prvního a druhého druhu a integrály v komplexní proměnné.
Definice
Mějme orientovanou křivku , která je definována rovnicemi pro . Na této křivce k nechť je definována funkce .
Křivku k rozdělíme na oblouků v bodech s parametry . Na každém oblouku zvolíme bod o souřadnicích a sestrojíme součty
kde je délka oblouku .
Největší z délek při daném dělení nazveme normou dělení , tzn. .
Pokud existuje takové číslo , resp. , resp. , že k libovolnému lze najít takové , že , resp. , resp. pro každé dělení , pro které bez ohledu na volbu bodů na , pak říkáme, že existuje křivkový integrál funkce po křivce k vzhledem k x, resp. k y, resp. k s, což zapisujeme vztahy
Integrál označujeme jako křivkový integrál prvního druhu, integrály jako křivkové integrály druhého druhu.
Je-li funkce spojitá na křivce k, pak uvedené integrály existují.
Za integrál druhého druhu se považuje také integrál
Je-li křivka k uzavřená, pak k označení křivkového integrálu po této křivce užíváme integrační znak .

Význam křivkových integrálů je demonstrován na obrázku. Obsah plochy, která je nad křivkou k ohraničena funkcí , je určen křivkovým integrálem prvního druhu, tedy integrálem . Obsah (orientovaného) průmětu této plochy do roviny , resp. , je určen integrálem , resp. .
Zobecnění křivkových integrálů na prostorové křivky je přímočaré. Je-li na oblasti definována spojitá funkce a křivka k zadaná parametricky vztahy pro , pak křivkový integrál prvého druhu zapíšeme
Křivkové integrály druhého druhu pak mají tvar
Vlastnosti křivkových integrálů
Je-li k orientovaná křivka, kterou lze rozložit na dvě souhlasně orientované křivky , pak pro křivkové integrály druhého druhu platí
a podobně pro křivkové integrály prvního druhu
Jsou-li na křivce k definovány funkce , pak pro libovolné konstanty
Označme jako křivku, která má opačnou orientaci než křivka . Při změně orientace křivky změní integrály druhého druhu své znaménko, tzn.
Integrály prvního druhu při změně orientace znaménko nemění, tzn.
Komplexní analýza
V komplexní analýze se operuje s křivkovými integrály z funkce komplexní proměnné přes křivky v komplexní rovině. Křivkový integrál z holomorfní funkce f(z) po C1 křivce γ(t) , kde t je její parametr probíhající interval <a,b>
kde se integruje zvlášť reálná a imaginární část. Jde-li o uzavřenou křivku, potom se používá značení
Komplexní křivkové integrály lze zpravidla snadno počítat pomocí primitivní funkce, jako (reálné) křivkové integrály II. druhu, pomocí Greenovy věty, Cauchyovy věty, reziduové věty, nebo pomocí Cauchyova vzorce. Pokud integrační křivka splývá na některém svém úseku s reálnou osou, lze v určitých případech pomocí komplexních integrálů počítat integrály reálné.
Příklad
Mějme funkci f(z)=1/z a křivku C definovanou jako jednotkovou kladně orientovanou kružnici se středem v počátku, která je parametrizována jako eit, kde parametr t probíhá <0, 2π>:
- ,
což lze rovněž ověřit Cauchyovým vzorcem.
Vektorový počet
Ve vektorovém počtu hrají důležitou roli především integrály prvního druhu (tedy integrály ze skalárního pole podél křivky) a integrály druhého druhu (integrály z vektorového nebo obecně tenzorového pole podél křivky).
Integrál prvního druhu
Nechť f je skalární pole Rn→R spojité po částech C1 podél křivky γ parametrizované zobrazením r(t) <a,b>→Rn, pro které je r'(t) nenulové pro každé t. Potom křivkový integrál prvního druhu
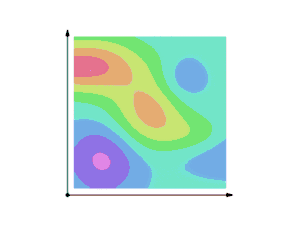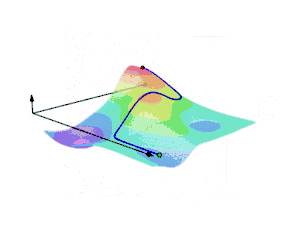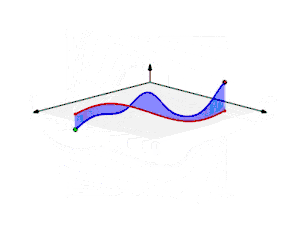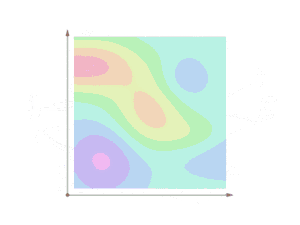
 Oranžová křivka C zobrazuje trajektorii částice uvnitř vektorového pole. Částice se pohybuje z bodu a do bodu b podél křivky a probíhá vektorovým polem F. Níže napravo sledujeme vektor z pohledu částice. Při změně směru se šipky os otáčejí. Modrá šipka znázorňuje aktuální orientaci částice vzhledem k poli F. Dole se zelenou barvou tvoří křivka podle směru cesty částice (křivka C). Vytvořená křivka zelenou barvou je ekvivalentní křivkovému integrálu.
Oranžová křivka C zobrazuje trajektorii částice uvnitř vektorového pole. Částice se pohybuje z bodu a do bodu b podél křivky a probíhá vektorovým polem F. Níže napravo sledujeme vektor z pohledu částice. Při změně směru se šipky os otáčejí. Modrá šipka znázorňuje aktuální orientaci částice vzhledem k poli F. Dole se zelenou barvou tvoří křivka podle směru cesty částice (křivka C). Vytvořená křivka zelenou barvou je ekvivalentní křivkovému integrálu.
Výsledná hodnota integrálu nezávisí na parametrizaci (integruje se podle elementu délky křivky), jen na křivce, podél které se integruje. Integrál skalárního pole po křivce vzniklé napojením dvou křivek v jednom bodě je součtem jednotlivých integrálů podél napojených křivek. Hodnota integrálu nezávisí na směru integrace (orientaci křivky). Integrál z funkce 1 je roven délce křivky:
Integrál druhého druhu
Nechť A je vektorové pole Rn→Rn spojité po částech C1 podél křivky γ parametrizované zobrazením r(t) <a,b>→Rn, pro které je r'(t) nenulové pro každé t. Potom křivkový integrál druhého druhu je
Absolutní hodnota integrálu nezávisí na parametrizaci, jen na orientaci křivky, podél které se integruje. Integrál vektorového pole po křivce vzniklé napojením dvou stejně orientovaných křivek v jednom bodě je součtem jednotlivých integrálů podél napojených křivek. Hodnota integrálu při změně směru integrace (orientace křivky) změní znaménko.
Transformace integrálu II. druhu
Integrál 2. druhu lze vždy převést na integrál 1. druhu z tečné souřadnice daného vektorového pole:
Za jistých dodatečných předpokladů lze křivkový integrál II. druhu převést na rozdíl potenciálů anebo na plošný integrál II. druhu.
Počítáme-li křivkový integrál II. druhu z konzervativního pole (nevírové, je gradientem nějaké funkce F) na křivce s počátečním bodem a koncovým bodem , lze psát
.
Integrál zde tedy nezávisí na cestě (křivce), ale jen na počátečním a koncovém bodu (a hodnotách potenciálu v nich).
Počítáme-li křivkový integrál II. druhu z nekonzervativního pole (vírového) po uzavřené křivce (tzv. cirkulaci), můžeme použít klasickou Stokesovu větu:
.
Související články
Externí odkazy
 Obrázky, zvuky či videa k tématu křivkový integrál na Wikimedia Commons
Obrázky, zvuky či videa k tématu křivkový integrál na Wikimedia Commons  Kniha Integrování/Výpočet reálných integrálů pomocí reziduové věty ve Wikiknihách
Kniha Integrování/Výpočet reálných integrálů pomocí reziduové věty ve Wikiknihách- STRMISKA, Martin. Aplikace křivkového integrálu. Zlín: Univerzita Tomáše Bati ve Zlíně, 2015, 75s. Dostupné také z: http://hdl.handle.net/10563/34231. Univerzita Tomáše Bati ve Zlíně. Fakulta aplikované informatiky, Ústav automatizace a řídicí techniky.