Legendreovy polynomy
Legendreovy polynomy jsou polynomy reálné proměnné definované na intervalu , které popsal Adrien-Marie Legendre roku 1782. Přitom je polynom stupně . Legendreovy polynomy se používají především v matematické fyzice a lze je definovat několika různými vzájemně ekvivalentními způsoby. Jedním z nich je požadovat, aby
- pro platilo (podmínka vzájemné ortogonality Legendreových polynomů);
- pro každé platilo (normující podmínka).
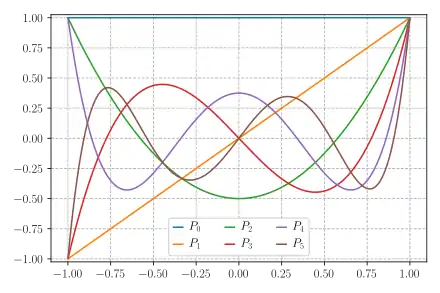
Legendreovy polynomy jsou zvláštním případem Gegenbauerových polynomů, které zase jsou zvláštním případem Jacobiho polynomů, jednoho z klasických polynomiálních systémů matematiky. Legendreovy polynomy sudého stupně jsou sudé funkce a Legendreovy polynomy lichého stupně jsou liché funkce.
Prvních několik Legendreových polynomů je:
Vlastnosti
Rodriguesova formule a její důsledky
Pro Legendreovy polynomy platí Rodriguesova formule (1818)
jež umožňuje odvodit další vzorce, vyjadřující tyto polynomy explicitně, například
Generující funkce a rekurentní vztah
Legendre své polynomy původně definoval pomocí generující funkce, tedy jako koeficienty Taylorova rozkladu:
Derivováním této rovnice podle a algebraickými úpravami lze odvodit Bonnetovu rekurzivní formuli
Legendre své polynomy objevil v souvislosti se studiem Newtonova potenciálu[1] (gravitační potenciál hmotného bodu nebo Coulombův potenciál bodového náboje), který lze rozložit na sumu těchto polynomů:
kde r a r′ jsou délky vektorů x a x′ a γ je úhel mezi těmito vektory. Vyjádření může být užitečné například integrujeme-li potenciál přes spojitou distribuci hmoty nebo náboje.
Legendreova diferenciální rovnice a úplnost
Legendreovy polynomy jsou řešeními diferenciální rovnice, pojmenované rovněž po Legendreovi:
Z toho plyne, že tyto polynomy jsou vlastními vektory odpovídajícího diferenciálního operátoru:
z čehož lze dále podle Sturmovy–Liouvilleovy teorie odvodit, že jde o úplný a ortogonální systém polynomů na definičním intervalu.
Jako úplný a ortogonální systém polynomů mají Legendreovy polynomy tyto vlastnosti:
kde je Kroneckerovo delta, rovné jedné, pokud a nule jinak.
Máme-li po částech spojitou funkci na intervalu , tak suma
konverguje v průměru k pro , pokud vezmeme koeficienty jako
Reference
- LEGENDRE, A.-M. Mémoires de Mathématiques et de Physique, présentés à l'Académie Royale des Sciences, par divers savans, et lus dans ses Assemblées. Paris: [s.n.], 1785. Kapitola Recherches sur l'attraction des sphéroïdes homogènes, s. 411–435. (French)
Externí odkazy
 Obrázky, zvuky či videa k tématu Legendreovy polynomy na Wikimedia Commons
Obrázky, zvuky či videa k tématu Legendreovy polynomy na Wikimedia Commons