Matematický důkaz

Ve všech vědeckých disciplínách s výjimkou matematiky jsou teorie posuzovány podle míry souladu s reálným světem a podle toho, nakolik přesně dokážou vysvětlovat a předpovídat reálné jevy. Nové teorie jsou budovány tak, aby odpovídaly experimentálně zjištěným datům. Jsou-li s těmito daty v souladu, jsou prohlášeny za správné. Je-li za nějaký čas vyslovena hypotéza, o jejíž platnosti současná teorie není schopna rozhodnout, provede se experiment, podle jehož výsledku se tato hypotéza buďto odvrhne, nebo zabuduje do uznávané teorie. Pokud se později objeví experimentální data, která jsou ve sporu se stávající teorií, je tato teorie odvržena a nahrazena teorií novou. Tento způsob ověřování hypotéz a budování teorií se nazývá induktivní.[2]

Příkladem induktivního důkazu může být způsob zdůvodnění tvrzení „Zítra ráno vyjde slunce.“ Ze zkušenosti naší i našich předků víme, že slunce vyšlo již mnohotisíckrát. Naproti tomu nemáme žádné zprávy o tom, že by nějaké ráno slunce nevyšlo. Navíc slunce poslední dobou nevykazuje žádné nezvyklé chování, které by napovídalo tomu, že je s ním něco jinak, než kdykoli v zaznamenané historii. Na základě těchto skutečností tedy usoudíme, že se zcela zanedbatelnou možností omylu slunce zítra ráno opět vyjde.

Induktivní dokazování však může být velice zrádné. Například v klasické mechanice je přijímáno za pravdivé tvrzení známé jako druhý Newtonův pohybový zákon, které tvrdí „Jestliže na těleso působí síla, pak se těleso pohybuje se zrychlením, které je přímo úměrné působící síle a nepřímo úměrné hmotnosti tělesa.“ Toto tvrzení odpovídalo až do druhé poloviny 19. století všem prováděným experimentům, a bylo tudíž považováno za pravdivé – induktivně dokázané. Poté, co na přelomu 19. a 20. století některé experimenty prokázaly, že pohyb světla se neřídí Newtonovými zákony, bylo toto tvrzení spolu s celou klasickou mechanikou odvrženo a nahrazeno teorií relativity. Podle této teorie vyvolává síla působící na těleso pohybující se rychlostí blízkou rychlosti světla jen minimální zrychlení a zbytek vložené energie způsobuje zvýšení hmotnosti tělesa.

Z posledního příkladu je patrné, že induktivně dokázané tvrzení nemůže být nikdy považováno za zcela nezpochybnitelné. Žádné, byť sebevětší, množství experimentálních dat potvrzujících toto tvrzení totiž nemůže zaručit, že nějaký v budoucnu provedený experiment s ním nebude ve sporu.

Naproti tomu deduktivní důkaz je takový, v němž je dané tvrzení dokázáno ze stanovených předpokladů pouze na základě logických úvah. Navíc tyto logické úvahy jsou rozděleny do konečně mnoha kroků, z nichž v každém je odvozeno pouze jediné tvrzení bezprostředně vyplývající z dříve odvozených. Z těchto důvodů je deduktivně dokázané tvrzení pravdivé, jsou-li pravdivé předpoklady, z nichž bylo odvozeno. Tato pravdivost je navíc zcela nezpochybnitelná, neboť důkaz lze rozdělit do konečně mnoha kroků, z nichž každý je pouhým bezprostředním logickým důsledkem dříve dokázaných tvrzení a jako takový tedy nezpochybnitelný.

Všechny druhy matematických důkazů od samotných historických počátků tohoto pojmu ve starověkém Řecku až po současnost, přes celou šíři nejrůznějších důkazových metod, jsou důkazy deduktivními.[3]

Uvažujme tvrzení: „Součin každých dvou lichých přirozených čísel je liché přirozené číslo.“

Vyzkoušíme-li několik nízkých přirozených čísel, zjistíme, že pro ně tvrzení platí: 1 · 1 = 1, 1 · 3 = 3, 3 · 1 = 3, 3 · 3 = 9, 3 · 5 = 15, …. Podobně bychom například s použitím počítače mohli ověřit, že tvrzení platí pro všechna čísla menší než 1 000 000, pokud by nám to nestačilo, mohli bychom tuto hranici zvýšit libovolně vysoko, například na 10^{1 000 000} (číslo začínající jedničkou za níž následuje 1 000 000 nul), a vždy bychom zjistili, že tvrzení platí. Po určité době takovýchto zvyšování hranice bychom již mohli uznat, že jsme vyzkoušeli dost příkladů na to, abychom si byli téměř stoprocentně jistí správností našeho tvrzení. Tím jsme toto tvrzení dokázali induktivně. Nikdy si však nemůžeme být zcela jisti, že nějaký protipříklad neleží těsně za číslem, na kterém jsme testování ukončili (toto bývá nazýváno problém horizontu).

Naproti tomu deduktivní důkaz je následující. Je-li m liché číslo, je m − 1 číslo sudé, tedy existuje celé číslo k takové, že m − 1 = 2 · k. Za k totiž stačí zvolit (m − 1) / 2, což je celé číslo právě díky sudosti m − 1. Pak m = 2 · k + 1. Obdobně zdůvodníme, že pro n liché existuje celé číslo l, že n = 2 · l + 1. Pak součin m · n je roven (2 · k + 1) · (2 · l + 1) = 4 · k · l + 2 · k + 2 · l + 1. Protože 4 · k · l + 2 · k + 2 · l je zjevně sudé, je m · n liché, což jsme chtěli dokázat. Až nyní si můžeme být stoprocentně jisti tím, že tvrzení platí. Jsou-li totiž dána dvě lichá čísla, platí pro ně každý jednotlivý krok důkazu, a tedy i jeho závěr.

Hypotéza prvočíselných dvojic je dosud (červenec 2011) nedokázané tvrzení z oblasti teorie čísel, podle kterého existuje nekonečně mnoho prvočísel p takových, že i p + 2 je prvočíslo. Dvojice takových čísel (p, p + 2) se nazývá prvočíselná dvojice.

Největší dosud známá prvočíselná dvojice je (65 516 468 355· 2 ^333 333 − 1; 65 516 468 355· 2^333 333 + 1), obě čísla této dvojice mají (v desítkové soustavě) 100 355 cifer.[4] Přestože jsou známy takto veliké příklady prvočíselných dvojic, není možné považovat hypotézu za deduktivně (matematicky) prokázanou, neboť je možné, že žádná další větší prvočíselná dvojice již nikdy nalezena nebude – jednoduše proto, že neexistuje. Nicméně předpokládá se (a nutno dodat, že nejen kvůli zde naznačenému induktivnímu důkazu), že tvrzení platí. Jeho důkaz tak zůstává jedním z nejvyzývavějších problémů současné teorie čísel.[5]

Část Rhindova papyru – sbírky 84 vyřešených úloh pocházející z období mezi střední a novou říší ve starověkém Egyptě

Od starých Egypťanů a Babylóňanů nejsou dochovány žádné matematické důkazy v dnešním slova smyslu. Dochovalo se mnoho záznamů zachycujících řešení různých konkrétních problémů a úloh. Má se za to, že tyto problémy byly již natolik abstraktní, a tato řešení tak elegantní, že v jejich pozadí muselo stát hluboké porozumění dané oblasti zahrnující implicitně důkazy správnosti používaných metod.[3]

V Číně 5. až 3. století př. n. l. se kromě praktické matematiky rozvíjela také logika. Té se věnovala zejména škola následníků filosofa Mo Tiho, jejíž příslušníci se zabývali teorií poznání a svá tvrzení logicky dokazovali.[6] Jedním z nejvýznamnějších následníků Mo Tiho byl Kung-sun Lung žijící v první polovině třetího století před naším letopočtem.

Logický důkaz však nebyl v Číně dále rozvíjen. Mo Tiho učení bylo totiž za vlády dynastie Chan zcela vytlačeno konfucianismem a pozdější čínští filosofové se k němu již nikdy nevrátili.

Pojem deduktivního matematického důkazu má svůj původ ve starověkém Řecku.[3] Stejně jako celá tehdejší matematika byl i matematický důkaz velmi úzce spjat s geometrií. Nejstarší matematické důkazy pocházejí právě z této doby – dochovaly se ve třináctidílném Euklidově spisu Základy.

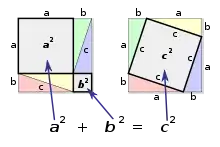
Matematický důkaz, tak jak ho známe v dnešní době, má své počátky v řecké geometrii rozvíjené pod vlivem Platónovy filosofie. Ovlivněni touto filosofií, snažili se tehdejší geometři odkrývat svět geometrických idejí a nazírat pravdu v něm obsaženou. V tomto pojetí matematický důkaz v dnešním smyslu slova ještě neexistoval. Jedinou možností, jak s naprostou jistotou zjistit pravdu o geometrickém světě, bylo tuto pravdu přímo nazírat – evidovat ji. Pokud se nějakému geometrovi podařilo evidovat platnost například Pythagorovy věty – tj. na malou chvíli skutečně zahlédl, že součet velikostí obsahů dvou čtverců nad odvěsnami pravoúhlého trojúhelníku je roven velikosti obsahu čtverce nad jeho přeponou, bylo to vždy jen na dobu, po kterou trvalo jeho soustředění. Jakmile pozornost polevila, zrak, kterým prohlížel do světa geometrických idejí, se zamlžil a evidence byla ztracena. Aby si kdykoli znovu mohl tuto evidenci zjednat a také aby stejnou možnost poskytl i ostatním matematikům, sepsal pak takový geometr návod, jak by měl člověk postupovat (tj. do jakých míst geometrického světa se dívat), aby znovu pravdivost Pythagorovy věty zahlédl. Takovéto návody, z nichž se později (v aristotelském pojetí geometrie) vyvinuly geometrické konstrukce, byly nejstaršími předchůdci matematických důkazů.

Platónské pojetí matematiky nebylo dlouhodobě udržitelné. Jak totiž docházelo k rozvoji geometrie, byly nově evidované pravdy ukryty stále hlouběji ve světě geometrických idejí. Geometr, který danou pravdu chtěl evidovat, tak musel pokaždé vynaložit veliké úsilí. Navíc u takto náročných evidencí bylo velmi obtížné udržet si po celou dobu nazírání do geometrického světa zrak zcela jasný a nezkalený. Takovéto evidence pak bylo dosaženo na pouhý zlomek sekundy, než se vše opět rozplynulo do mlhavé nejistoty, v níž geometr nevěděl, zda danou pravdu skutečně zahlédl, či zda to bylo jen zdání. Náročnost evidencí složitějších geometrických pravd byla do jisté míry dána i tím, že kdykoli chtěl geometr použít například Pythagorovu větu, musel ji nejprve znovu přivést k evidenci v daném konkrétním případě. Z těchto důvodů odstupovali někteří geometři (pravděpodobně aniž by si to uvědomovali) od platónského způsobu nazírání do světa idejí a pomalu se nadechovali ke kroku, který dal charakter celé matematice od jejich doby až do současnosti. Tímto krokem bylo vpuštění rozumu do světa matematiky. Pokud totiž geometr již mnohokrát evidoval Pythagorovu větu, mohl si být zcela jistý její pravdivostí. Potřeboval-li ji později použít pro evidenci jiné pravdy, uvědomil si, že není nutné znovu ji přivádět k evidenci v tomto konkrétním případě. Stačilo, že o její platnosti věděl a rovněž věděl, že pokud by ji nyní evidoval, mohl by již evidovat i pravdu, o kterou mu šlo. Tato rozumová úvaha tedy nahradila sled evidencí. Bylo to nahrazení nenápadné – kdykoli by si totiž geometr přál, mohl si být jistý, že na základě této úvahy by danou pravdu k evidenci přivedl. Přes tuto nenápadnost šlo však o zásadní krok. Geometrické pravdy již nemusely být pouze evidovány, stačilo rozumově zdůvodnit, že by (kdykoli si to bude někdo přát) evidovány být mohly. Tím se zrodil matematický důkaz.

Oxyrynchuský papyrus pocházející z let 75–125 n. l. Je na něm zachycen důkaz tvrzení pět z druhé knihy Euklidových Základů.

Aristotelův význam pro celou tehdejší i budoucí evropskou vědu je nesmírný. Trvalé a neměnné geometrické ideje byly pod jeho vlivem nahrazeny pouhými představami geometrických objektů. Matematika (i v této době stále ještě reprezentována téměř výhradně geometrií) provozovaná v područí Aristotelovy filosofie a logiky znala již logický důkaz jako úvahu probíhající v jazyce,[7] tzn. prostou jakýchkoli evidencí (neboť ideje, které jediné lze evidovat, již ve světě matematiky nebyly). Důležitým rysem důkazu začíná být v této době jeho vztah ke skutečným (rozuměj představitelným) objektům. Tato souvislost se dá nejlépe vyjádřit na vztahu bezespornosti a uskutečnitelnosti. Bezesporné jsou takové myšlené objekty, z jejichž vlastností nelze vyvodit logický spor (tj. nelze dokázat nějakou vlastnost a současně její negaci). Uskutečnitelné jsou naopak takové objekty, které je možné (alespoň v představě) realizovat. Základní logické pravidlo stanovené Aristotelem říká, že žádný objekt nemůže mít zároveň vlastnost i její negaci. Tedy myšlený objekt, který je sporný, nemůže být uskutečnitelný. Opačné tvrzení, tj. bezesporný objekt je uskutečnitelný, v této době za pravdivé uznáváno nebylo.[8] Například čtyři vzájemně kolmé úsečky sice nejsou dohromady ve sporu, avšak kvůli omezením kladeným trojrozměrným prostorem je uskutečnit ani si představit nelze.

V této době se také krystalizovaly základní druhy důkazových postupů známé jako klasické vzory logických důkazů.[9] Mezi tyto vzory patří důkaz přímý, nepřímý, rozborem případů a myšlenou konstrukcí (viz odstavec Druhy matematických důkazů).

Aristotelské pojetí matematiky a matematického důkazu je zachyceno v Euklidových spisech Základy, v nichž se také poprvé objevuje myšlenka axiomatické výstavby matematiky ve formě Euklidových postulátů.

Římská matematika obecně nebyla nikdy rozvinutá a v podstatě jen přešlapovala na té úrovni znalostí, na níž jí zanechali Řekové. Pragmatická římská společnost uznávala pouze tu část matematiky, která se hodila pro aplikace ve stavitelství a vojenství. Zájem o čistou matematiku včetně pojmu matematického důkazu byl v podstatě nulový.

Stránka z knihy Hisáb al-džabr wa-l-muqábala

Matematika jako celek zejména v raném středověku prožívala období temna. Řecké pojetí matematiky a důkazu bylo dále provozováno pouze v Byzantské říši. Odtud se od 8. století s tímto pojetím seznamovali Arabové (značný vliv na arabskou matematiku měla i matematika indická). V plné síle se arabská matematika projevila v Al-Chorezmího díle Hisáb al-džabr wa-l-muqábala (حساب الجبر و المقابلة‎) v němž byly položeny základy algebry a s tím souvisejícího nového druhu matematického důkazu – důkazu výpočtem. Tento nový druh důkazu byl používán také později italskými renesančními matematiky při hledání obecných řešení algebraických rovnic.

Pro pojetí matematického důkazu v Evropě v období od 16. do první poloviny 19. století je podstatný pojem oboru, na němž byla tehdejší matematika založena.[10] Obor je vymezení jisté třídy uskutečnitelných objektů takové, že o každém objektu lze rozhodnout (alespoň teoreticky), zda do tohoto oboru patří či nikoli. Příklady oborů mohou být obory přirozených čísel, derivovatelných reálných funkcí, ale i takové, u nichž není známo jak přesně vypadají, či zda nejsou dokonce prázdné, jako například obor všech prvočíselných dvojic větších než 10^1 000 000.

V této době byl v matematice stále výrazně patrný Aristotelův vliv – matematické objekty neměly trvalé bytí jako platónské ideje, bylo je možné pouze si představit nebo je myslet (uskutečnit je v představě resp. v myšlení). V uskutečnění získávaly tyto objekty své bytí, po ochabnutí pozornosti přestávaly opět existovat. Obor tedy nebyl považován za nějaký soubor trvale existujících objektů, nýbrž za jisté vyznačení těch objektů – stávajících, již zaniklých, dosud nevytvořených i takových, které nikdy existovat nebudou – jež do tohoto oboru patří (a duálně i těch, které do něj nepatří). Důkaz tvrzení „Pro každý objekt z daného oboru platí…“ tedy v tomto smyslu znamenal prokázání tohoto tvrzení pro každý objekt (třeba i takový, který nebude nikdy uskutečněn) tohoto oboru. Toto pojetí se shoduje se současným chápáním sousloví „pro každé“. Na rozdíl od toho věta „Existuje objekt z daného oboru, že platí…“ není v tomto pojetí tvrzením. Její platnost totiž není trvalá, neboť v oboru tak, jak zde byl vyložen, jistý objekt existuje právě tehdy, když je uskutečněn v myšlení nějakého člověka. Jakmile myšlenka zanikne, přestává takový objekt existovat, a tedy platnost této věty se může s časem měnit. Abychom získali tvrzení musíme si počínat obezřetněji a formulovat příslušnou větu následovně: „Je uskutečnitelný objekt z daného oboru, že platí…“. Takovéto tvrzení pak lze dokázat pouze jedním způsobem, a to tak, že se požadovaný objekt uskuteční – zkonstruuje. Jediným způsobem dokazování existenčních tvrzení tedy byl v této době důkaz konstrukcí. Ryze existenční, nekonstruktivní důkaz z výše zmíněných důvodů používán nebyl a ani být nemohl. Kromě konstruktivního důkazu se za správný stále ještě považoval i důkaz opřený o geometrický názor, bez něhož se tehdy u jistých tvrzení (např. u Bolzanovy věty) matematici neobešli.

Podle Bolzana je Bůh na rozdíl od člověka schopen vidět všech nekonečně mnoho členů cauchyovské posloupnosti naráz, a tedy přímo eviduje i bod na přímce, ke kterému se členy této posloupnosti blíží. Takový bod tedy existuje, ačkoli žádný člověk ho není schopen zkonstruovat.
_{(Upravený obraz Williama Blakea The ancient of days)}

Význam českého filosofa a matematika Bernarda Bolzana pro vývoj nejen pojetí matematického důkazu, ale celé matematiky spočívá v nahrazení oborů trvale existujícími seskupeními objektů. Z těchto seskupení se později vyvinul pojem množiny, který se stal ústředním pojmem matematiky 20. století. Poznamenejme na okraj, že při nahrazování nekonečných oborů seskupeními se Bolzano musel vypořádat s problémem aktuálního nekonečna (tj. problémem, zda reálně existuje nekonečné množství nějakých objektů). Tento problém dokázal vyřešit pouze použitím teologie, když zdůvodnil, že aktuálně nekonečné množství se nachází v mysli křesťanského Boha.[11]

Pokud jsou dána trvale existující seskupení objektů, má již (na rozdíl od případu oborů) věta „Existuje objekt z daného seskupení, že platí…“ trvalý charakter a je tedy tvrzením. Toto tvrzení je pak možné dokazovat dvěma způsoby. První možností je postupovat stejně jako v případě oborů, tj. požadovaný objekt zkonstruovat. Novou možností, která se nyní nabízí, je prokázat pouhou existenci žádaného objektu bez nutnosti nějaký takový objekt sestrojovat. Tento nový druh důkazu se nazývá nekonstruktivní či také ryze existenční. Typickým příkladem použití nekonstruktivního důkazu je Cantorův důkaz existence transcendentních čísel, při kterém se ukáže, že všech algebraických čísel je pouze spočetně mnoho (lze je očíslovat přirozenými čísly), zatímco všech reálných čísel je nespočetně mnoho (nelze je očíslovat). Protože tedy je reálných čísel více než algebraických, musí alespoň jedno transcendentní existovat. Z tohoto důkazu není však vůbec jasné, jak nějaké transcendentní číslo najít.

Již někteří dřívější filosofové a teologové (Giordano Bruno, Rodrigo de Arriaga) zdůvodňovali užitím předpokladu Boží existence, že objekty, které nejsou vzájemně v logickém sporu, již musí být uskutečnitelné (a to v Boží mysli).[12] Toto tvrzení, které je obrácením klasické Aristotelovy poučky o neuskutečnitelnosti sporného, se později v matematice ujalo. Jeho formalizací v řeči moderní matematické logiky je tzv. Gödelova věta o úplnosti.

V důsledku Bolzanovy práce se do oblasti zkoumání matematiky dostaly i takové objekty, jejichž existence je sice dokazatelná, ale není je možné nijak zkonstruovat. Příkladem takového objektu je například spojitá funkce, která nemá v žádném svém bodě derivaci (tečnu ke grafu), objevená nezávisle nejprve Bolzanem a později Weierstrassem. Poněkud vágně řečeno, graf takové funkce je možné nakreslit jedním tahem, ale v každém bodě tohoto grafu je zlom, tj. nikoli „hladký oblouček“, ale „špička“. Ještě podivnějším příkladem může být Peanova křivka, což je prostá spojitá křivka definovaná na intervalu (0,1), jejíž obraz vyplňuje celý čtverec (0,1) × (0,1), nebo funkce z reálných do reálných čísel, která na každém intervalu nabývá všech reálných hodnot. Tyto a jim podobné příklady zcela odporují lidské intuici – Charles Hermite o Bolzanově-Weierstrassově funkci a dalších podobných příkladech dokonce prohlásil: „Odvracím se s děsem a hrůzou od této politováníhodné záplavy spojitých funkcí bez derivace.“[13] Podstatnější pro další vývoj matematického důkazu je však reakce Henriho Poincarého, který se ve spise La valeur de la Science ptá „Jak nás může intuice v tomto případě tak zklamat?“[13]

Poincarého údiv je pochopitelný, neboť objevením výše uvedených příkladů došlo k něčemu, co do té doby nemělo v matematice obdoby. Geometrický názor a intuice se dostaly do sporu s dokazatelnými tvrzeními. Aby se zabránilo spornosti celé matematiky, bylo nezbytné odmítnout intuici a názor jako důkazové prostředky. Důkazy mnohých základních tvrzení, zejména matematické analýzy a geometrie, však byly v této době na názoru založeny, bylo tedy nutné postavit je opět na pevný základ. Tímto pevným základem se stala axiomatická metoda používaná již v antickém Řecku Euklidem v jeho Základech. Avšak i Eukleidés vycházel (pravděpodobně aniž by si to uvědomoval) do značné míry z intuice – o tom svědčí například fakt, že zatímco Euklidových postulátů je pouze pět, David Hilbert ve své práci Grundlagen der Geometrie (Základy geometrie) používá k axiomatizaci geometrie postulátů 21. I řecká axiomatická metoda se tedy ukázala jako nedostačující, a než na ní mohla být založena celá matematika, musela být zcela oproštěna od intuice.

Místem, kde se v řeckém pojetí intuice používala nejčastěji, byl matematický důkaz. Ačkoli v geometrii byly za axiomy vybírány i mnohé z nejzřejmějších pravd, aby se tak použití názoru omezilo na minimum, samotný způsob logického odvozování důsledků z těchto axiomů axiomatizován nebyl a logický úsudek byl užíván zcela volně. Aby zcela vyloučili intuici (a tím i veškerou nejistotu) z matematiky, museli tedy matematici druhé poloviny 19. století axiomatizovat samotný pojem matematického důkazu. Zároveň s tím docházelo v důsledku snahy po odstranění nepřesnosti vycházející z (intuitivního) používání přirozeného jazyka k formalizaci tohoto pojmu, tj. nahrazení přirozeného jazyka jazykem symbolickým. V pracích Davida Hilberta, Gottloba Frega a dalších byl postupně vyvinut formální symbolický jazyk dostatečně bohatý, aby vyjádřil všechna matematická tvrzení, a pojem formálního důkazu, který umožňoval dokazovat formálně zapsaná tvrzení (tzv. formule) s použitím pouze několika málo odvozovacích pravidel nazývaných logické axiomy, tj. bez nejmenšího vlivu intuice či názoru. Matematický důkaz se tak stal jasně definovaným pojmem natolik přesným, že po nástupu moderní výpočetní techniky mohla být jeho správnost ověřena i pouhým algoritmicky pracujícím počítačem.

Historický vývoj dovedl matematický důkaz do takového stádia přesnosti, že jeho správnost může být ověřena pouhým počítačem. V současné době dokonce existují tzv. systémy automatického dokazování vět, což jsou počítačové programy schopné konstruovat důkazy matematických tvrzení. Tyto programy jsou sice mnohdy schopny dokazovat i ne zcela triviální věty, přesto však jsou stále daleko od stádia, kdy by je bylo možné v praxi použít. Mezi odbornou matematickou veřejností neexistuje jednoznačný názor na to, zda je možné vyvinout program, který by mohl v matematickém dokazování konkurovat člověku.

Dalším způsobem zapojení počítačů do oblasti dokazování vět jsou důkazy řízené člověkem, v nichž je však počítač použit jako pomocník v těch místech důkazu, kde není potřeba invence ani abstraktní myšlení. Nejznámějším takovým použitím počítače je důkaz věty o čtyřech barvách (viz níže).

Poznamenejme, že lze dokázat matematické věty, podle kterých nemůže existovat žádný počítačový program, který by dovedl o každém tvrzení rozhodnout, zda je či není dokazatelné (viz rozhodnutelnost).

Neformální důkaz je důkaz v přirozeném jazyce vycházející z daných předpokladů a pravidel rozumu. Z historických důvodů se rozlišuje několik základních druhů (neformálních) důkazů.

Přímý důkaz je postup, při kterém je dokazované tvrzení odvozeno přímou aplikací definic, předpokladů a dříve dokázaných tvrzení, jinak řečeno je odvozeno metodou „jestliže… pak…“ či „…tedy…“.

Nepřímý důkaz je metoda sloužící k prokazování tvrzení typu „jestliže A, pak B“, při které se prokáže „jestliže ne B, pak ne A“. Má úzký vztah k důkazu sporem – každý nepřímý důkaz může být snadno převeden na důkaz sporem.

Důkaz sporem (lat. reductio ad absurdum) se zakládá na použití chybného předpokladu, který je posléze doveden ke sporu (je z něj odvozeno zjevně nepravdivé tvrzení). Stane-li se tak, je prokázána neplatnost daného předpokladu a tedy platnost jeho opaku. Důkaz sporem má blízko k nepřímému důkazu – každý nepřímý důkaz může být snadno převeden na důkaz sporem.

Důkaz indukcí spočívá v prokázání nějakého tvrzení typu „pro všechny objekty jisté třídy platí…“ způsobem, při němž se objekty dané třídy rozdělí do několika (většinou nekonečně mnoha) podtříd, které se uspořádají do posloupnosti a ukáže se o nich:

1. (první krok) Pro všechny objekty z první podtřídy platí…
2. (indukční krok) Jestliže platí … pro všechny objekty z předcházejících podtříd, pak platí… i pro všechny objekty z podtřídy bezprostředně za nimi následující.

Existuje mnoho druhů důkazů indukcí:

• matematická indukce (všechny podtřídy jsou jednoprvkové a posloupnost spočetná)
• transfinitní indukce (všechny podtřídy jsou jednoprvkové a posloupnost může být libovolné kardinality)
• fundovaná indukce
• indukce dle složitosti

Důkaz myšlenou konstrukcí je metodou dokazování existenčních tvrzení „existuje X takové, že…“, při které se sestrojí (zkonstruuje) objekt X, pro nějž… platí. Tento druh důkazu se také někdy nazývá důkaz uvedením příkladu.

Při důkazu rozborem případů dochází k rozdělení zkoumané situace na konečně mnoho případů a prokázání požadovaného tvrzení pro každý z těchto případů zvlášť. Typickým příkladem jsou geometrické důkazy, kde se například pro platnost obecné věty o trojúhelníku uvažují tři případy trojúhelníku ostroúhlého, pravoúhlého a tupoúhlého nebo důkazy, v nichž se rozlišují případy, kdy dané číslo je kladné, nulové nebo záporné.

Nekonstruktivní důkaz nějakého existenčního tvrzení „existuje X takové, že…“ je takový důkaz, který sice prokáže existenci takového X, ale nelze z něj žádným způsobem obdržet ani jediný příklad objektu, který by za X mohl být zvolen. Tento druh důkazu je dnes již většinou uznáván za správný, ale v minulosti (zejména na přelomu 19. a 20. století) mnozí významní matematici proti takovému způsobu dokazování protestovali a tvrzení dokázaná tímto způsobem neuznávali. V dnešní době existuje v matematice samostatný směr tzv. konstruktivismus, který se snaží prokazovat všechna tvrzení konstruktivně (viz intuicionistická logika). Průkopníky na poli nekonstruktivních důkazů byli Georg Cantor (s důkazem existence transcendentních čísel) a zejména David Hilbert. Problematika nekonstruktivních důkazů úzce souvisí s axiomem výběru a existencí (bezesporností) aktuálního nekonečna.

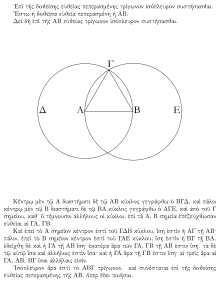
Geometrický důkaz Pythagorovy věty

Geometrický důkaz je takový důkaz, který využívá metod geometrie. Jeho názornost je značnou měrou dána možností geometrické představy, přesný geometrický důkaz však nesmí být na takovémto názoru založen. Geometrické důkazy jsou nejčastěji využívány v samotné geometrii, ale velmi často také v matematické analýze a teorii čísel.

Důkaz výpočtem – sled rovností doplněný slovním komentářem pocházející z knihy Gabriela Cramera Introduction a l’analyse de lignes courbes algébriques

Důkaz výpočtem slouží k prokázání tvrzení, která jsou tvaru rovnosti, nerovnosti či nějaké soustavy předchozích dvou. K požadovanému výsledku se dospívá z předpokladů výpočtem, tj. opakovanou aplikací základních aritmetických a algebraických pravidel a různých odhadů. První důkazy výpočtem se objevily při řešení algebraických rovnic v díle perského matematika Al-Chorezmího. V současné době se důkaz výpočtem nejvíce uplatňuje v matematické analýze, lineární algebře, teorii pravděpodobnosti, numerické matematice a příbuzných oborech, kde tento postup tvoří hlavní část důkazů mnoha tvrzení. Je však v menší míře užíván snad ve všech matematických disciplínách s výjimkou geometrie.

Formální důkaz je takový důkaz, který není prováděn v přirozeném jazyce, ale v jazyce symbolickém – formálním. Kvůli minimalizaci míry nepřesnosti, která bývá u neformálního důkazu vysoká, jsou pro účely formálního důkazu chápána všechna tvrzení jako konečné posloupnosti znaků (tzv. formule, případně segmenty) a je zaveden systém pravidel stanovující, jak lze s těmito posloupnostmi zacházet. Tento systém pravidel se nazývá logický kalkulus. Dva nejpoužívanější kalkuly jsou hilbertovský a gentzenovský. Každý z těchto kalkulů sestává z logických axiomů, které vyjadřují základní vlastnosti logických spojek a kvantifikátorů, a z odvozovacích pravidel, která stanovují, jakým způsobem lze z předpokladů odvozovat jejich důsledky.

Formální důkaz v hilbertovském kalkulu je definován jako konečná posloupnost formulí z nichž jedna, obvykle poslední, vyjadřuje dokazované tvrzení, a jejíž každý člen je buďto

• logickým axiomem
• vlastním axiomem teorie, v níž je dokazováno
• odvozen z předchozích členů podle jednoho z odvozovacích pravidel (viz Hilbertovský kalkulus).

Gentzenovský kalkulus se od hilbertovského liší tím, že nejsou dokazovány formule, ale tzv. sekventy, což jsou symboly tvaru ${\displaystyle <A\Rightarrow B>}$, kde ${\displaystyle A}$, ${\displaystyle B}$ jsou konečné množiny formulí. Symbol ${\displaystyle <A\Rightarrow B>}$ má význam „Platí-li všechny formule z A, pak platí alespoň jedna formule z B“. Za důkaz formule ${\displaystyle \varphi }$ se tedy považuje důkaz sekventu ${\displaystyle <\emptyset \Rightarrow \{\varphi \}>}$.

Velká Fermatova věta je následující tvrzení:

Neexistují kladná celá čísla x, y a z taková, že platí xⁿ + yⁿ = zⁿ, pro nějaké přirozené číslo n větší než 2.

Toto tvrzení je jednou z nejslavnějších vět v celých dějinách matematiky. Historie důkazu této věty sahá od středověkých arabských matematiků až po samotný konec 20. století, pokusy o její důkaz pravidelně a výrazně ovlivňovaly rozvoj celé matematické vědy, zejména algebry a algebraické teorie čísel.[14]

Pravděpodobně již středověcí arabští matematikové věděli o platnosti velké Fermatovy věty pro případ n = 3, jejich důkazy se však nedochovaly.[15] Nejstarší dochovaný důkaz pro tento případ pochází od Leonharda Eulera.

Samotný Pierre de Fermat dokázal případ n = 4 tak, že ke každému případnému řešení této rovnice sestrojil řešení menší. Tím získal nekonečnou klesající posloupnost přirozených čísel a tedy spor.

Roku 1825 vyřešili Peter Dirichlet a Adrien-Marie Legendre případ n = 5 a roku 1839 Gabriel Lamé n = 7.

V roce 1847 dokázal Ernst Kummer Fermatovu větu pro všechna regulární prvočísla, mezi něž patří všechna prvočísla menší než 100 s výjimkou 2, 37, 59 a 67.

Andrew Wiles

Obecný případ velké Fermatovy věty dokázal v roce 1995 Andrew Wiles poté, co byla v jeho domnělém důkazu z roku 1993 nalezena chyba. Důkaz velké Fermatovy věty je výjimečný v mnoha ohledech. Jeho délka je více než 100 stran tištěného textu, vznikl soustavnou devítiletou prací jediného matematika, hlavně však v sobě propojuje mnoho různých někdy i dosti od sebe vzdálených oblastí matematiky – teorii diofantických rovnic, modulární formy, algebraickou geometrii, Galoisovu teorii a další.[16] Díky tomu bývá považován za významný krok směrem k naplnění tzv. Langlandsova programu propojení teorie čísel a teorie reprezentací. Je zároveň vynikající ukázkou toho, jak obtížný může být důkaz jednoduše formulovaného tvrzení.

Věta o čtyřech barvách říká, že každou mapu v rovině lze obarvit čtyřmi barvami tak, aby každá dvě sousední území měla odlišnou barvu. Domněnku, že tomu tak je, vyslovil již v roce 1852 mladý matematik Francis Guthrie. V roce 1878 vešla tato domněnka ve všeobecnou známost, když Arthur Cayley požádal všechny účastníky setkání Londýnské matematické společnosti, aby se ji pokusili dokázat. Domněnka však odolávala všem snahám o důkaz ještě dalších téměř sto let. Až v roce 1976 oznámili Kenneth Appel a Wolfgang Haken, že důkaz nalezli.

Příklad mapy v rovině obarvené čtyřmi barvami.

Appelovi a Hakenovi se podařilo redukovat celý problém čtyř barev na pouhých konečně mnoho případů, které bylo nutno vyřešit. Těchto případů však bylo tolik (přesně 1936), že jejich ručním prověřováním by jeden člověk mohl strávit celý svůj život, aniž by je všechny vyřešil. Proto bylo prověření těchto případů zadáno počítači, který nad nimi strávil více než 1200 hodin strojového času. Toto použití počítače pro důkaz matematické věty vyvolalo ve své době živou polemiku. Žádný člověk totiž nemohl již nikdy ověřit správnost důkazu – bylo sice možné ručně překontrolovat správnost počítačového programu, který jednotlivé případy prověřoval, to ovšem nevylučovalo možnost hardwarové chyby, která mohla celý důkaz znehodnotit. Na obranu počítačového dokazování bylo argumentováno, že u takto složitých a dlouhých důkazů je pravděpodobnost hardwarové chyby sice nenulová ale jistě mnohem menší než pravděpodobnost, že se obdobné chyby dopustí člověk.[17] V současné době je věta o čtyřech barvách obecně považována za dokázanou a proti použití počítače v matematických důkazech nejsou vznášeny větší námitky.

Nutno dodat, že Appel s Hakenem věřili, že jejich důkaz je jen prvním z řady, v nichž budou podstatným způsobem využity počítače.[17] Takových důkazů však není mnoho; lze uvést např. důkaz neexistence projektivní roviny řádu 10, důkaz Robbinsovy domněnky a několik důkazů týkajících se vítězných strategií v některých konečných hrách.

Věta o klasifikaci konečných jednoduchých grup říká, že každá konečná jednoduchá grupa spadá buďto do jedné z 18 nekonečných skupin grup nebo je jednou z 26 takzvaných sporadických grup. Tím tedy tato věta plně charakterizuje všechny konečné jednoduché grupy. Kvůli ohromné náročnosti jejího důkazu bývá v angličtině také nazývána „Enormous theorem“.

Důkaz této věty nebyl nikdy uveřejněn v celku. Sestává z více než 500 článků od přibližně 100 autorů uveřejněných v nejrůznějších matematických časopisech převážně mezi lety 1955 a 1983. Odhaduje se, že celková délka důkazu je 10 000–15 000 stran tištěného textu.[18] Taková rozsáhlost může vyvolat (podobně jako u věty o čtyřech barvách) pochybnosti o správnosti důkazu. Žádný matematik totiž pravděpodobně nepřečetl tento důkaz celý, a tedy nikdo na světě nemůže sám o sobě tvrdit, že v něm není chyba. Každá jednotlivá část důkazu publikovaná v průběhu téměř třiceti let však byla mnoha matematiky přečtena a uznána za správnou. Proto je tento důkaz všeobecně považován za správný, ačkoli žádný konkrétní člověk nikdy jeho správnost neověřil a velmi pravděpodobně ani v budoucnu neověří.

Vzhledem k neuvěřitelné délce důkazu je vysoce pravděpodobné, že obsahuje mnoho drobných chyb a nepřesností. Jeden z hlavních autorů důkazu Michael Aschbacher k tomu řekl: „Pravděpodobnost chyby v klasifikační větě je prakticky 1. Na druhou stranu pravděpodobnost, že každá jedna z těchto chyb by nebyla snadno opravitelná, je prakticky nula a protože důkaz je konečný, pravděpodobnost, že věta neplatí, je velmi blízko nule. Jak čas ubíhá a my máme příležitost blíže se s důkazem seznamovat, naše důvěra v něj může jedině růst.“[18]

• ŠVEJDAR, Vítězslav. Logika, neúplnost, složitost a nutnost. Praha: Academia, 2002. ISBN 80-200-1005-X.

• VOPĚNKA, Petr. Rozpravy s geometrií. Praha: Panorama, 1989. ISBN 80-7038-031-4.
• VOPĚNKA, Petr. Vyprávění o kráse novobarokní matematiky. Praha: Práh, 2004. ISBN 80-7252-103-9.

• Axiom
• Důkaz (právo)
• Gödelovy věty o neúplnosti
• Postulát
• Premisa
• Teorie důkazu

• Obrázky, zvuky či videa k tématu matematický důkaz na Wikimedia Commons
• Téma Matematický důkaz ve Wikicitátech

• Co je to (Fregovská) logika? (pdf) – krátký článek Jaroslava Peregrina nejen o matematickém důkazu ve Fregově pojetí

• The History and Concept of Mathematical proof (pdf) – článek o historii a filosofickém opodstatnění matematického důkazu
• Notes on methods of proof – stránky obsahující popis několika nejdůležitějších důkazových metod
• Coq a IMPS – dva systémy automatického dokazování vět volně ke stažení