Čtverec

• Čtverec je pravoúhlý rovnostranný rovnoběžník.
• Všechny vnitřní úhly jsou pravé → pravoúhlý.
• Všechny strany jsou shodné → rovnostranný.
• Protilehlé strany jsou rovnoběžné → rovnoběžník.
• Úhlopříčky čtverce jsou shodné a navzájem kolmé, půlí jeho úhly i sebe navzájem.
• Čtverci lze jakožto pravidelnému mnohoúhelníku opsat i vepsat kružnici, je to zároveň tětivový čtyřúhelník i tečnový čtyřúhelník. Je to tedy dvojstředový čtyřúhelník a středy kružnice opsané i vepsané splývají.
• Čtverec (jako zvláštní případ obdélníka) má ze všech obdélníků s daným obvodem největší obsah a ze všech obdélníků s daným obsahem nejmenší obvod.
• Euklidovskou rovinu lze definovat jako dvojrozměrný prostor, v němž existuje čtverec.
• Bez ohledu na jeho zobrazení (stojící na jednom ze svých rohů nebo natočený rohem k pozorovateli) zůstává čtverec čtvercem a nemění se v kosočtverec[1].
• Někdy bývá považován za zvláštní případ obdélníku (pravoúhlý rovnoběžník) nebo kosočtverce (rovnostranný rovnoběžník).

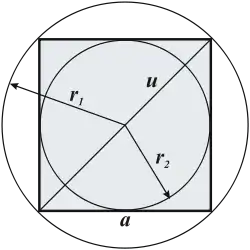
Čtverec s úhlopříčkou, vepsanou a opsanou kružnicí

Pomocí délky strany čtverce ${\displaystyle a}$ lze vyjádřit

• obvod

  ${\displaystyle \ O=4a}$

• obsah

  ${\displaystyle \ S=a^{2}}$

• délka úhlopříčky

  ${\displaystyle u=a{\sqrt {2}}}$

• poloměr kružnice opsané

  ${\displaystyle r_{1}={\frac {u}{2}}}$

• poloměr kružnice vepsané

  ${\displaystyle r_{2}={\frac {a}{2}}}$