Matice
Matice je v matematice obdélníkové či čtvercové schéma čísel nebo nějakých matematických objektů – prvků matice (též elementů matice). Obsahuje obecně m řádků a n sloupců. Hovoříme pak o matici typu .
Část matematiky, která využívá matice, je označována jako maticový počet.
Matice se často využívají pro vyjádření obecné rotace vektorů, transformace vektorů od jedné báze k bázi jiné, k výpočtu soustav lineárních rovnic, či k vyjádření operátorů v kvantové mechanice.
Označení prvků matice
Prvky matice jsou označeny indexy udávajícími řádek a sloupec, v nichž se prvek nalézá. Prvek v i-tém řádku a j-tém sloupci matice A se obvykle značí . Potom -tý řádek matice obsahuje vodorovnou -tici prvků , kde a -tý sloupec matice obsahuje svislou -tici čísel , kde .
Např. a53 leží v pátém řádku a třetím sloupci. Indexy se píší buďto oba dole jako a53, nebo první nahoře a druhý dole jako a53, což má význam, jakmile je potřeba rozlišovat kovariantní a kontravariantní indexy, zejména operujeme-li s maticemi jako s tenzory. Tedy matici m krát n zapíšeme jako:
Pro zjednodušení se také používá zápisu
- .
Potřebujeme-li zdůraznit počet řádků a sloupců, lze také použít zápis
- .
Pokud nehrozí chyba (např. indexy jsou jednociferné), lze vynechat čárku oddělující oba indexy, tj. .
Příklad
Matice
je obdélníková matice velikosti 4 × 3. Prvek matice a23 nebo a23 je 7.
Operace s maticemi
Sčítaní, násobení skalárem, a transpozice
| Operace | Definice | Příklad |
|---|---|---|
| Sčítání | Součet A+B dvou matic A and B typu m×n je matice typu m×n, sčítání probíhá po prvcích:
|
|
| Násobení skalárem | α-násobek matice A je součin čísla α (nazývané skalár) a matice A, který se spočítá vynásobením každého prvku matice A číslem α:
|
|
| Transpozice | Transpozice matice A typu m×n je matice AT typu n×m (někdy také značená Atr or tA), která vznikne výměnou řádků a sloupců:
|
Násobení matic
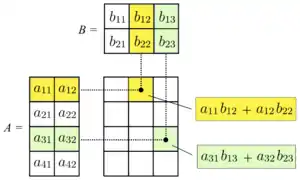
Násobení dvou matic je definováno pouze pokud má levá matice stejný počet sloupců jako má pravá matice řádků. Pokud A je matice typu m×n a B je matice typu n×p, pak jejich součin AB je matice typu m×p, jejíž prvky jsou skalárním součinem příslušného řádku A a příslušného sloupce B:
- kde 1 ≤ i ≤ m a 1 ≤ j ≤ p.
- Například podtržený prvek 2340 součinu se spočítá jako (2 · 1000) + (3 · 100) + (4 · 10) = 2340:
Maticové násobení splňuje rovnost (AB)C = A(BC) (asociativitu), a rovnosti (A + B)C = AC + BC a C(A + B) = CA + CB (distributivitu zleva a zprava), pokud mají matice takové rozměry, aby součiny byly definovány. Součin AB může být definován, aniž by bylo definováno BA, pokud A a B jsou matice typu m×n a n×k, kde m ≠ k. Pokud jsou oba součiny definovány, nemusí být stejné. Pro obecné matice platí:
- AB ≠ BA
Maticové násobení není komutativní, na rozdíl od součinu (racionálních, reálných, nebo komplexních) čísel. Příklad dvou matic, které spolu nekomutují:
- zatímco
Mimo obvyklý maticový součin existují ještě jiné operace s maticemi, které lze považovat za určitý druh násobení, jako například Hadamardův součin anebo Kroneckerův součin.
Rovnost
- O dvou maticích A, B prohlásíme, že jsou si rovny, pokud jsou stejného typu (stejný počet řádků i sloupců) a každý prvek matice A je roven odpovídajícímu prvku matice B. Rovnost zapíšeme
Rozdíl
- Rozdíl dvou matic A, B (stejného typu) je nová matice R:
Prvky matice R jsou pak určeny vztahem
Lineární kombinace
- Obecně lze pro matice , které jsou stejného typu, definovat lineární kombinaci matic
- ,
- kde prvky matice určuje výraz
Vlastnosti a základní pojmy
Algebraické vlastnosti prostorů matic
Obvykle se předpokládá, že prvky matice jsou z nějakého okruhu nebo tělesa. Označme jej (obvykle nebo ). Množina všech čtvercových matic tvoří asociativní algebru, která se nazývá maticová algebra, značí se , , nebo apod. Pro je nekomutativní a její centrum je izomorfní (je tvořeno násobky jedničkové matice). Je jednoduchá, t.j. nemá žádné netriviální oboustranné ideály. Navíc každá konečně rozměrná jednoduchá asociativní algebra (nad nějakým tělesem) je izomorfní maticové algebře. Každá volba báze -dimenzionálního prostoru nám dává izomorfizmus . Jediná ireducibilní reprezentace této asociativní algebry je její definující reprezentace na .
Matice je invertovatelná, právě když její determinant je nenulový (toto má smysl, i kdyby byly prvky matice z obecného komutativního okruhu, a analogické tvrzení lze zformulovat i v kvaternionových maticích).
Množina všech regulárních (t.j. invertovatelných) matic tvoří grupu, která se označuje . Pro je reduktivní. Její jednoduchá podgrupa je grupa matic s jedničkovým determinantem .
Hodnost matice
Hodnost matice se dá definovat jako počet lineárně nezávislých řádků (předpokládáme, že prvky matice jsou prvky nějakého tělesa). Platí, že počet lineárně nezávislých sloupců matice je stejný jako počet lineárně nezávislých řádků.
Diagonála matice
Prvky , leží na tzv. hlavní diagonále matice. Hlavní diagonála je tedy tvořena všemi prvky , kde .
Prvky , leží na tzv. vedlejší diagonále. Vedlejší diagonála je tedy tvořena všemi prvky , kde .
Pokud se hovoří o diagonále matice, je tím obvykle myšlena hlavní diagonála.
Důvod dvojího značení
Matice se obvykle používají k zápisu lineárních zobrazení mezi vektorovými prostory. Předpokládejme, že matice přiřadí vektoru v, který má souřadnice (v nějaké bázi) vektor, který má (v nějaké bázi cílového prostoru) souřadnice (symbolicky Av=w).
Užíváme-li matice k operaci s vektory v Euklidovském prostoru, nebo kdykoliv se příslušný skalární součin chová stejně jako v Euklidovském prostoru a předpokládáme, že jediné změny souřadnicových systémů, které uvažujeme, jsou rotace a zrcadlení, pak není potřeba rozlišovat polohu indexů a řádkové a sloupcové vektory lze mezi sebou libovolně zaměňovat. Jakmile se však skalární součin chová jinak (např. Diracova notace v kvantové mechanice), anebo uvažujeme i jiné transformace souřadnic než rotace a zrcadlení, pak se při přechodu do jiných souřadnic typicky jinak transformují vektory jako duální vektory. Sloupce matice se chovají jako vektory, kdežto řádky matice jako duální vektory, neboli lineární formy. Ve fyzice se pak obvykle souřadnice vektorů píšou nahoru a souřadnice duálních vektorů dolů.
Tento koncept lze matematicky formalizovat, pokud řekneme, že matice je prvek prostoru zapsán v nějakých bázích prostorů . Protože ale , můžeme chápat matici jako tenzor typu (1,1) a u tenzorů se píšou kovariantní složky dolů a kontravariantní nahoru. Pak se matice bude při přechodu k novým souřadnicím v prostorech V a W transformovat „správně“.
Matice ale nereprezentují jen lineární zobrazení mezi vektorovými prostory. Do matice se taky dá zapsat bilineární forma, která dvěma vektorům přiřadí číslo. Pak to odpovídá tenzoru typu (0,2) a při přechodu do jiných souřadnic se transformuje jako tenzor typu (0,2). V tomto případě bychom prvky matice značili () (oba indexy dolů).
Pokud však matice reprezentuje něco jiného (třeba systém lineárních rovnic, na který se nemusíme dívat jako na maticovou rovnici a nepotřebujeme vědět, jak se transformuje při změně souřadnic), pak nemá smysl horní a dolní indexy rozlišovat.
Druhy matic
| Přehled některých typů matic | ||
| Nad | Nad | vlastnost |
| hermitovská | symetrická | |
| unitární | ortogonální | |
| regulární (invertibilní) | ||
- Matice typu je tvořena jedním řádkem a bývá označována jako řádková matice.
- Matice typu je tvořena jedním sloupcem a bývá označována jako sloupcová matice.
- Je-li , pak matici označujeme jako čtvercovou matici -tého řádu (stupně). Pro bývá matice označována jako obdélníková.
- Pokud jsou všechny prvky matice nulové, tzn. pro všechna , označujeme matici jako nulovou.
- Matici, která má nenulové prvky pouze na hlavní diagonále, tzn. pro a pro , nazýváme diagonální maticí. Prvky diagonální matice lze vyjádřit pomocí Kroneckerova symbolu
- ,
kde jsou diagonální prvky matice. Pokud pro všechny diagonální prvky diagonální matice platí , jedná se o jednotkovou matici , pro jejíž prvky platí
- Matici, která má všechny prvky pod hlavní diagonálou nulové, označujeme jako horní trojúhelníkovou matici. Taková matice má tvar
Podobně označujeme jako dolní trojúhelníkovou matici takovou matici, která má všechny prvky nad diagonálou nulové.
- Jsou-li i konečná čísla, označujeme matici jako konečnou.
- Matici, která vznikne z matice vzájemnou výměnou řádků a sloupců, označujeme jako transponovanou matici a značíme . Pro jednotlivé prvky transponované matice platí
- Pokud je transponovaná matice shodná s původní maticí, tzn. , pak matici označujeme jako symetrickou. Pro prvky symetrické matice platí
- .
- Matici označujeme jako antisymetrickou, platí-li pro všechny prvky této matice vztah
- .
- Pokud každý prvek matice nahradíme prvkem k němu komplexně sdruženým , pak získáme matici , kterou označujeme jako komplexně sdruženou matici.
- Pokud je matice komplexně sdružená rovna původní matici, tzn. , pak matici nazýváme reálnou maticí.
- Provedeme-li na matici transpozici a komplexní sdružení, získáme matici hermiteovsky sdruženou (někdy též psáno „hermitovsky“, podle Charlese Hermita). Hermiteovsky sdruženou matici značí různí autoři různě, zpravidla některým z následujících způsobů
(poslední z možných zápisů se může snadno plést s tzv. Moore-Penroseovou pseudoinverzí matice)
- Pokud je hermiteovsky sdružená matice rovna původní matici, tzn. , říkáme, že matice je hermitovská (též samosdružená nebo samoadjungovaná). Každá takováto matice má všechna vlastní čísla reálná. (důkaz indukcí s využitím základní věty algebry a Gram-Schmidtovy ortogonalizace)
- Matice je inverzní maticí k matici , pokud platí
- ,
kde je jednotková matice.
- Matici , ke které existuje inverzní matice, označujeme jako regulární matici. Není-li matice regulární, pak ji označujeme jako singulární.
- Matici označujeme jako unitární, jestliže inverzní matice je rovna matici hermiteovsky sdružené , tzn.
- Adjungovaná matice k matici A je transponovaná matice algebraických doplňků matice A.
Použití
Matice jako zápis lineárního zobrazení
Matice představují nejjednodušší nástroj, jak popsat v souřadnicích lineární zobrazení z prostorů V do prostoru W, pokud máme na prostoru V zvolenou bázi a na prostoru W bázi . Matice zobrazení vytvoříme tak, že její i-tý sloupec bude zápis souřadnic obrazu vektoru zapsaného v bázi .
Matice přechodu
Matice jsou užitečný nástroj na spočtení souřadnic vektoru v nějaké bázi, pokud známe jeho souřadnice v jiné bázi. Pokud a jsou dvě báze, pro které platí , neboli
pak matice se nazývá matice přechodu od báze k bázi . Pro souřadnice pak platí
kde jsou souřadnice libovolného vektoru v bázi a jsou jeho souřadnice v bázi a je inverzní matice k matici .
Duální báze k a (pokud je píšeme do sloupců) se transformují stejně jako souřadnice a souřadnice duálních vektorů v duálních bázích (pokud je píšeme do řádků) stejně jako původní bázové vektory.
Matice jako zápis bilineární formy
Matice představují jednoduchý nástroj, jak popsat v souřadnicích bilineární zobrazení (například skalární součin) (obvykle nebo ), pokud máme na prostoru V zvolenou bázi a na prostoru W bázi . Matice zobrazení A vytvoříme tak, že , kde (.) je příslušná bilineární forma. Pak v souřadnicích platí .
Systémy lineárních rovnic
Systém m rovnic o n neznámých se dá zapsat elegantně do matice jako
Řešení se nezmění, pokud budeme provádět následující úpravy:
- Výměna dvou řádků
- Vynásobení řádku nenulovým číslem
- Přičtení násobku nějakého řádku k jinému řádku
Takovými operacemi je možno systém značně zjednodušit (viz Gaussova eliminace).
Zkoumání lineární nezávislosti vektorů
Pokud mám nějakou sadu vektorů zapsanou v souřadnicích, můžu tyto vektory (resp. jejich souřadnicové vyjádření) zapsat jako řádky pod sebe a vznikne matice. Lineární obal řádků matice se nezmění, pokud budu dělat následující úpravy:
- Výměna dvou řádků
- Vynásobení řádku nenulovým číslem
- Přičtení násobku nějakého řádku k jinému řádku
Pokud vhodnými úpravami dokážu udělat někde nulový řádek, původní vektory jsou lineárně závislé (viz též Gaussova eliminace).
Řešení obyčejných diferenciálních rovnic
Obyčejná homogenní diferenciální rovnice s konstantními koeficienty, anebo systém rovnic s konstantními koeficienty, se dá přepsat na maticovou rovnici , kde je vektor neznámých a A je matice. Řešení je pak vektorový prostor generovaný sloupci matice dané maticovou funkcí .
Další použití
V matematice a fyzice:
- Jacobiho matice
- Hessova matice
- Wronského matice
- incidenční matice grafu
Ve statistice:
- Matice dat (zcela obecná tabulka popisující závislost jedné veličiny na druhé)
- Korelační matice
- Stochastická matice
- kontingenční tabulky
V kvantové mechanice:
- Zápis operátorů do matic
- Matice hustoty (popis smíšeného stavu systému)
- Pauliho matice
V populační biologii:
- Leslieho model
Odkazy
Související články
Externí odkazy
 Obrázky, zvuky či videa k tématu matice na Wikimedia Commons
Obrázky, zvuky či videa k tématu matice na Wikimedia Commons  Slovníkové heslo matice ve Wikislovníku
Slovníkové heslo matice ve Wikislovníku- M. Zahradník, L. Motl: Pěstujeme lineární algebru
- Učebnice lineární algebry na webu (anglicky)
- Autar Kaw, Introduction to Matrix Algebra
- Maticová kalkulačka
- Operace s maticemi v R (determinant, stopa, inverzní, adjungovaná, transponovaná)*
- Sčítání a násobení matic