Lorentzova grupa
Lorentzova grupa je ve fyzice a matematice grupa všech Lorentzových transformací Minkowského prostoru, klasické i kvantové prostředí všech (negravitačních) fyzikálních jevů. Lorentzova grupa je pojmenována po nizozemském fyzikovi Hendriku Antoonu Lorentzovi.

K zákonům, rovnicím a teoriím, které respektují Lorentzovy symetrie, patří např.:
- kinematické zákony speciální teorie relativity
- Maxwellovy rovnice pole v teorii elektromagnetismu
- Diracova rovnice v teorii elektronu
- Standardní model fyziky částic
Lorentzova grupa vyjadřuje základní symetrii prostoru a času všech známých základních přírodních zákonů. Fyzikální zákony jsou Lorentzovým invariantem také v relativistické fyzice v případech uvažujících dostatečně malé oblasti prostoročasu, kde jsou gravitační variance zanedbatelné, a ve speciální teorii relativity.
Základní vlastnosti
Lorentzova grupa je podgrupou Poincarého grupy – grupy všech izometrií Minkowského prostoru. Lorentzovy transformace jsou právě ty izometrie, které ponechávají počátek souřadnicového systému pevný. Lorentzova grupa je tedy podgrupa izotropie grupy izometrií Minkowského prostoročasu. Z tohoto důvodu se Lorentzova grupa někdy nazývá homogenní Lorentzova grupa zatímco Poincarého grupa je někdy nazývaný nehomogenní Lorentzova grupa. Lorentzovy transformace jsou příklady lineárních transformací; obecné izometrie Minkowského prostoročasu jsou afinními zobrazeními. Lorentzova grupa může být matematicky popsána jako Neurčitá ortogonální grupa O(1,3), Lieova grupa, která zachovává kvadratickou formu
na R4. Tato kvadratická forma je, když ji převedeme na maticový tvar (viz klasická ortogonální grupa), interpretována ve fyzice jako metrický tenzor prostoročasu Minkowského.
Lorentzova grupa je šestirozměrná nekompaktní neabelovská Lieova grupa, která není souvislá. Čtyři souvislé komponenty nejsou jednoduše souvislé.[1] komponenta identity (tj. komponenta obsahující identitu) Lorentzovy grupy je sama grupou a často se nazývá omezená Lorentzova grupa a značí se SO+(1,3). Omezená Lorentzova grupa sestává z těch Lorentzových transformací, které zachovávají orientaci prostoru a směr času. Jeho fundamentální grupa má řád 2 a jeho univerzální pokrytí, Neurčitá spinová grupa Spin(1,3), je izomorfní jak se speciální lineární grupou SL(2, C) tak se symplektickou grupou Sp(2, C). Tyto izomorfismy umožňují použití Lorentzovy grupy ve velkém množství matematických struktur důležitých pro fyziku, především pro spinory. V relativistické kvantové mechanice a v kvantové teorii pole, je obvyklé nazývat SL(2, C) Lorentzovou grupou, s chápat, že SO+(1,3) je její určitá (vektorová) reprezentace. S grupou SL(2, C) jsou také izomorfní bikvaterniony používané v geometrické algebře, .
Omezená Lorentzova grupa také se objevuje jako bodová grupa symetrií určité obyčejné diferenciální rovnice.[které?]
Souvislé komponenty
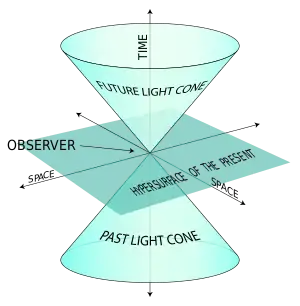
Díky tomu, že Lorentzova grupa O(1,3) je Lieovou grupou, je jednak grupou a zároveň připouští topologický popis jako hladké variety. Jako varieta má čtyři souvislé komponenty. Intuitivně to znamená, že sestává ze čtyř topologicky oddělených částí.
Čtyři souvislé komponenty lze klasifikovat dvěma transformačními vlastnostmi, které mají jejich prvky mít:
- Některé prvky jsou při Lorentzových transformacích invertujících čas obráceny, například Minkowského prostor ukazující do budoucnosti je invertován na vektor ukazující do minulosti
- Některé prvky mají obrácenou orientaci kvůli nevlastní Lorentzově transformaci, například určité tetrády (vierbein)
Lorentzovy transformace, které zachovávají směr času, se nazývají ortochronní. Podgrupa ortochronních transformací se často označuje O+(1,3). Transformace, které zachovávají orientaci, se nazývají vlastní, a jako lineární transformace mají determinant +1. (Nevlastní Lorentzovy transformace mají determinant −1.) Podgrupa vlastních Lorentzových transformací se označuje SO(1,3).
Podgrupa všech Lorentzových transformací zachovávajících orientaci i směr času se nazývá vlastní, ortochronní Lorentzova grupa nebo omezená Lorentzova grupa a značí se symbolem SO+(1, 3). (Někteří autoři používají označení SO(1,3) nebo dokonce O(1,3) pro SO+(1, 3).)
Množinu čtyř souvislých komponent lze považovat za grupu jako faktorovou grupu O(1,3)/SO+(1,3), která je izomorfní s Kleinovou čtyřgrupou. Každý prvek v O(1,3) lze zapsat jako semidirektní součin vlastní, ortochronní, transformace a prvku diskrétní grupy
- {1, P, T, PT}
kde P a T jsou operátory parity a obrácení toku času:
- P = diag(1, −1, −1, −1)
- T = diag(−1, 1, 1, 1).
Libovolnou Lorentzovu transformaci lze tedy zadat jako vlastní, ortochronní, Lorentzovu transformaci spolu s dalšími dvěma bity informace, které vybírají jednu ze čtyř souvislých komponent. Tato struktura je typická pro konečněrozměrné Lieovy grupy.
Omezená Lorentzova grupa
Omezená Lorentzova grupa je komponenta identity Lorentzovy grupy, což znamená, že sestává ze všech Lorentzových transformací, které lze zapojit do identity spojitou křivkou ležící v grupě. Omezená Lorentzova grupa je souvislá normální podgrupa úplné Lorentzovy grupy se stejným počtem rozměrů, v tomto případě se šesti rozměry.
Omezená Lorentzova grupa je generovaná obyčejnými prostorovými rotacemi a Lorentzovými transformacemi (které jsou rotacemi v hyperbolickém prostoru, který obsahuje časupodobný směr [2]). Protože každou vlastní, ortochronní Lorentzovu transformaci lze zapsat jako součin rotací (daných třemi reálnými parametery) a boost (také daných třemi reálnými parametry), je třeba 6 reálných parametrů pro zadání libovolné vlastní ortochronní Lorentzovy transformace. To je jeden z důvodů, proč je omezená Lorentzova grupa šestirozměrná. (Viz také Lieova algebra Lorentzových grup.)
Množina všech rotací vytváří Lieovu grupu izomorfní s obyčejnou rotační grupou SO(3). Množina všech boostů však netvoří podgrupu, protože složení dvou boostů obecně nevede k jinému boostu. (Místo toho je dvojice nekolineárních boostů ekvivalentní s boostem a rotací a toto se týká Thomasovy rotace.) Boost v nějakém směru nebo rotace kolem nějaké osy, generuje jednoparametrickou podgrupu.
Povrchy tranzitivity
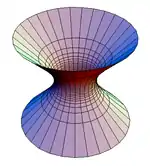
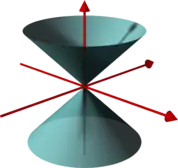
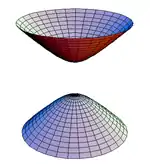
Pokud grupa G působí na prostor V, pak povrch S ⊂ V je povrch tranzitivity, pokud S je invariantní při G, tj. ∀g ∈ G, ∀s ∈ S: gs ∈ S a pro jakýkoli dva body s1, s2 ∈ S existuje g ∈ G tak, že gs1= s2. Podle definice Lorentzovy grupy zachovává kvadratickou formu
Povrchy tranzitivity ortochronní Lorentzovy grupy O+(1, 3), Q(x) = const. prostoročasu jsou následující:[3]
- Q(x) > 0, x0 > 0 je horní část hyperboloidu se dvěma povrchy. Body na této části jsou od počátku souřadnicového systému odděleny budoucím časoprostorovým vektorem.
- Q(x) > 0, x0 < 0 je spodní část tohoto hyperboloidu. Body na této části jsou minulé časoprostorové vektory.
- Q(x) = 0, x0 > 0 je horní část světelného kužele, budoucí světelný kužel.
- Q(x) = 0, x0 < 0 je spodní část světelného kužele, minulý světelný kužel.
- Q(x) < 0 je hyperboloid tvořený jedním povrchem. Body na této ploše jsou časoprostorově odděleny od počátku souřadnicového systému.
- Počátek souřadnicového systému x0= x1= x2= x3= 0.
Tyto povrchy jsou trojrozměrné, takže obrázky nejsou věrné, ale věrně odpovídají faktům o O+(1, 2). Pro úplnou Lorentzovu grupu jsou povrchy tranzitivity pouze čtyři, protože transformace T změní horní část hyperboloidu (kuželu) na dolní a naopak.
Tato pozorování představují dobrý počátek pro hledání všech nekonečnědimenzionálních unitárních reprezentací Lorentzovy grupy, respektive Poincarého grupy, pomocí metody indukované reprezentace.[4] Začneme se „standardním vektorem“, jeden pro každý povrch tranzitivity a pak se práme, která podgrupa zachovává tyto vektory. Tyto podgrupy fyzikové nazývají akce grupy na množině. Problém pak je v zásadě redukovaný na snazší problém hledání reprezentací malých grup. Například standardní vektor v jednom z ramen hyperboly lze vhodně zvolit jako (m, 0, 0, 0). Pro každé m ≠ 0 prochází vektor právě jednou částí (plochou). V tomto případě je malá grupa SO(3), ortogonální grupa, jejíž všechny reprezentace jsou známy. Přesná nekonečněrozměrná unitární reprezentace, při které transformace částic jsou částí své klasifikace. Ne všechny reprezentace mohou odpovídat fyzikálním částicím (pokud víme). Standardní vektory na hyperbolách s jednou částí by odpovídaly tachyonům. Částice na světelném kuželu jsou fotony a hypotetické gravitony. „Částicí“ odpovídající počátku souřadnicového systému je vakuum.
Homomorfismy a izomorfismy
Omezená Lorentzova grupa SO+(1, 3) je homomorfní nebo izomorfní s několika dalšími grupami. Tyto homomorfismy hrají klíčovou roli v objasňování různých jevů ve fyzice.
- Speciální lineární grupa SL(2,C) je dvojitým pokrytím Lorentzovy grupy. Tento vztah je velmi používaný pro vyjadření Lorentzovské kovariance Diracovy rovnice a kovariance spinorů.
- Symplektická grupa Sp(2,C) je izomorfní s SL(2,C); používá se pro konstrukci Weylových spinorů, i pro vysvětlení, jak mohou mít spinory hmotnost.
- Spinová grupa Spin(1,3) je izomorfní s SL(2,C); používá se pro vysvětlení spinu a spinorů v pojmech Cliffordovy algebry, tedy objasnění, jak zobecnit Lorentzovu grupu na obecný případy v Riemannově geometrii, včetně teorie supergravitace a teorie strun.
- Omezená Lorentzova grupa je izomorfní s projektivní grupou PSL(2,C), která je zase izomorfní s Möbiovou grupou, což je grupa symetrií konformní geometrie na Riemannově sféře. Tento vztah je klíčový pro klasifikaci podgrup Lorentzovy grupy podle staršího klasifikačního schématu vyvinutého pro Möbiovu grupu.
Weylova reprezentace
Weylova reprezentace nebo spinorové zobrazení je dvojice surjektivních homomorfismů SL(2,C) na SO+(1,3), které při transformacích parity tvoří srovnaný pár, odpovídající levému a pravému chirálnímu spinoru.
Na Minkowského prostoročasu můžeme definovat akci SL(2,C) tak, že bod prostoročasu vyjádříme hermitovskou maticí 2×2 ve tvaru
pomocí Pauliho matic. Tato Weylova prezentace vyhovuje vztahu
Proto máme identifikovaný prostor Hermitovské matice (který je čtyřrozměrný, stejně jako reálný vektorový prostor) s prostoročasem Minkowského takovým způsobem, že determinant Hermitovské matice je druhá mocnina délky odpovídajícího vektoru v Minkowského prostoročasu. Prvek působí na prostoru Hermitovských matic přes
kde je Hermitovská transpozice . Tato akce zachovává determinant, a proto SL(2,C) působí na Minkowského prostoročasu jako (lineární) izometrie. Tvar s obrácenou paritou je
který se transformuje jako
Že jde o korektní transformaci, vyplývá z toho, že
zůstává invariantní vůči výše uvedené dvojici transformací.
Tato zobrazení jsou surjektivní a jádro každého z nich je dvouprvková podgrupa ±I. Díky první větě o isomorfismu je podílová grupa PSL(2,C) = SL(2,C) / {±I} izomorfní s SO+(1,3).
Zobrazení parity tato dvě pokrytí prohazuje. To znamená, že Hermitovská konjugace je automorfismus Tyto dvě různá pokrytí odpovídají dvěma různým chiralitním akcím Lorentzovy grupy na spinorech. Tvar bez pruhu odpovídá pravostranné spinorové transformaci zatímco tvar s pruhem odpovídá levostranné spinorové transformaci [pozn. 1]
Je důležité si všimnout, že tento pár pokrytí není zachován při kvantizaci; což vede ke zvláštnímu jevu chirální anomálie. Kvantizace porušuje klasické (tj. nekvantizované) symetrie Lorentzovy grupy; to říká Atiyahova–Singerova indexová věta.
Konvence značení
V fyzice se Lorentzova transformace obvykle značí jako tedy používat matici s prostoročasovými indexy Čtyřvektor lze z Pauliho matice vytvořit dvěma způsoby: jako a jako které se vztahují k paritní transformaci. Pamatujte, že
Je-li dána Lorentzova transformace pak dvojité pokrytí ortochronní Lorentzovy grupy uvedené výše lze zapsat jako
Zanedbáním dostaneme tvar
Paritně konjugovaný tvar je
Důkaz
Není okamžitě zjevné, že výše uvedený tvar je správným tvarem indexované notace. Částečně protože při práci v indexované notaci je docela snadné si náhodně plést Lorentzovu transformaci s její inverzí nebo její transpozicí. Tato nedorozumění se objevují způsobené identity se obtížně rozpoznává, pokud je napsané v indexovaném tvaru. Lorentzovy transformace nejsou tensory při Lorentzově transformaci! Tedy přímý důkaz této identity je užitečný, pro vytvoření jeho korektnost. To lze ukázat, když začneme identitou
kde , takže výše uvedené jsou pouze obvyklé Pauliho matice a je matice transpozice a je komplexní konjugace. Matice je
Napsaný jako čtyřvektor, vztah je
Tento transformace jako
Pokud vezmeme o jednu transpozici více, dostaneme
Symplektická grupa
Symplektická grupa Sp(2,C) je izomorfní s SL(2,C). Tento izomorfismus je zkonstruován tak, aby zachovával symplektický vektorový prostor na tj. ponechal tvar invariantní při Lorentzově transformaci. To můžeme vyjádřit takto. Symplektická grupa je definována jako
kde
Jiné běžné notace jsou pro tento prvek; někdy se používá, ale toto způsobuje nedorozumění s myšlenkou téměř komplexních struktur, které nejsou stejné, protože se transformují odlišně.
Je-li dána dvojice Weylových spinorů (které mají dvě složky)
invariantní bilineární tvar se tradičně zapisuje
Tento tvar je invariantem v Lorentzově grupě, takže pro máme
Tento vztah definuje určitý druh „skalárního součinu“ spinorů a často se používá pro definici Lorentzova invariantu hmotnostního členu v Lagrangiánech. Existují několik významných vlastností, které je třeba připomenout, protože jsou důležité pro fyziku. Jedním je, že a tak
Definiční relaci lze zapsat jako
což se blízce podobá definici relace pro Lorentzova grupa
kde je metrický tenzor pro Minkowského prostor a samozřejmě, stejně jako výše.
Pokrývací grupy
Protože SL(2,C) je jednoduše souvislá, jde o univerzální pokrývací grupu omezené Lorentzovy grupy SO+(1, 3). Kvůli omezení existuje homomorfismus SU(2) → SO(3). Speciální unitární grupa SU(2), která je izomorfní s grupou kvaternionů s jednotkovou normou, je také jednoduše souvislá, takže jde o pokrývací grupu grupy rotací SO(3). Každé z těchto pokrývacích zobrazení jsou dvojitým pokrytím v tom smyslu, že na každý prvek kvocientu se zobrazí právě dva prvky z pokrývací grupy. Často říkáme, že omezená Lorentzova grupa a rotační grupa jsou dvojitě souvislé. To znamená, že jejich fundamentální grupa je izomorfní s dvouprvkovou cyklickou grupou Z2.
Dvojitá pokrytí jsou charakteristická pro spinové grupy. Opravdu spolu s dvojitým pokrytím
- Spin+(1, 3) = SL(2, C) → SO+(1, 3)
- Spin(3) = SU(2) → SO(3)
máme dvojité pokrytí
- Pin(1, 3) → O(1, 3)
- Spin(1, 3) → SO(1, 3)
- Spin+(1, 2) = SU(1, 1) → SO(1, 2)
Tato spinoriální dvojí pokrytí jsou zkonstruována z Cliffordových algeber.
Topologie
Levé a pravé grupy v dvojitém pokrytí
- SU(2) → SO(3)
jsou deformační retrakty levých a pravých grup (v tomto pořadí) v dvojitém pokrytí
- SL(2,C) → SO+(1,3).
Ale homogenní prostor SO+(1,3)/SO(3) je homeomorfní s hyperbolickým 3-prostorem H3, takže máme vyjádřenou omezenou Lorentzovu grupu jako hlavní fibrovaný prostor s fibry SO(3) a bází H3. Protože druhý je homeomorfní s R3, zatímco SO(3) je homeomorfní s trojrozměrným reálným projektivním prostorem RP3, vidíme, že omezená Lorentzova grupa je lokálně homeomorfní se součinem RP3 a R3. Protože báze prostoru je kontraktibilní, lze ji rozšířit na globální homeomorfismus.[ujasnit]
Generátory boostů a rotací
Na Lorentzovu grupu lze pohlížet jako na podgrupu grupa difeomorfismů R4, a proto lze její Lieovu algebru identifikovat s vektorovým polem na R4. Konkrétně vektory, které generují izometrie na prostoru jsou jeho Killingovy vektory, které poskytují pohodlnou alternativu k levému invariantu vektorového pole pro výpočet Lieovy algebry. Můžeme zapsat sadu šesti generátorů:
- Vektorové pole na R4 generuje tři rotace i J,
- Vektorové pole na R4 generuje tři boosty i K,
Může být užitečné zde stručně připomenout, jak získat jednoparametrickou grupu z vektorového pole zapsaného ve tvaru lineárního diferenciálního operátoru prvního řádu jako například
Odpovídající počáteční úloha je
Řešení lze zapsat
nebo
v čemž snadno rozpoznáváme jednoparametrickou maticovou grupu rotací exp(i λ Jz) kolem osy z.
Derivováním podle grupového parametru λ a položením λ=0 v tomto výsledku získáme standardní matici,
která odpovídá vektorovému poli, se kterým jsme začali. To ukazuje, jak přecházet mezi maticovou a vektorovou reprezentací pole prvků Lieovy algebry. Tuto speciální roli hraje exponenciální zobrazení nejen pro Lorentzovu grupu ale pro Lieovy grupy obecně.
Obrácením postupu v předchozí části zjistíme, že Möbiovy transformace, které odpovídají našim šesti generátorům, vznikají z uplatnění exponenciálního zobrazení postupně η/2 (pro tři boosty) nebo (iθ/2)krát (pro tři rotace) tři Pauliho matice
Třídy konjugace
Protože omezená Lorentzova grupa SO+(1, 3) je izomorfní s Möbiovou grupou PSL(2,C), její třídy konjugace se také rozpadají do pěti tříd:
- Eliptické transformace
- Hyperbolické transformace
- Loxodromické transformace
- Parabolické transformace
- Triviální identické transformace
V článku o Möbiových transformacích je vysvětleno, jak se k těmto klasifikacím dospěje uvažováním pevných bodů Möbiových transformací v jejich akce na Riemannově sféře, která zde odpovídá nulovým vlastním prostorům omezené Lorentzovy transformace v jejich akci na Minkowského prostoročasu.
Příklad každého typu je uveden v jednotlivých podčástech níže spolu s vlivem jednoparameterické podgrupy, kterou generuje (například na vzhled noční oblohy).
Möbiovy transformace jsou konformní zobrazení Riemannovy sféry (neboli nebeské sféry). Pak konjugace s libovolným prvkem SL(2,C) postupně dávají následující příklady libovolné eliptické, hyperbolické, loxodromické a parabolické (omezené) Lorentzovy transformace. Vliv na linie toku odpovídajících jednoparametrických podgrup je transformovat vzorek viděný v příklady nějakou konformní transformací. Například eliptické Lorentzovy transformace mohou mít jakékoli dva různé pevné body na nebeské sféře, ale body stále tečou po kruhových obloucích z jednoho pevného bodu k druhému. Ostatní případy jsou podobné.
Eliptické transformace
Eliptický prvek SL(2,C) je
a jeho pevné body jsou ξ = 0, ∞. Pokud zapíšeme akci jako X ↦ P1 X P1† a shromáždíme členy, spinorové zobrazení jej konvertuje na (omezenou) Lorentzovu transformaci
Tato transformace pak reprezentuje rotace kolem osy z, exp(iθJz). Jednoparametrické podgrupa, kterou generuje, lze získat když θ nebo konstanta, ale reálná proměnná, rotační úhel.
Odpovídající spojité transformace nebeské sféry (až na identitu) vesměs sdílejí tytéž dva pevné body, severní a jižní pól. Všechny ostatní body transformace přesunuje po rovnoběžkách, takže při zvětšování θ dává tato grupa spojité rotace proti směru hodinových ručiček kolem osy z. Úhel zdvojnásobení zjevný v spinorovém zobrazení je charakteristickou vlastností spinorového dvojitého pokrytí.
Hyperbolické transformace
Hyperbolický prvek grupy SL(2,C) je
a má pevné body ξ = 0, ∞. Při stereografické projekci z Riemannovy sféry do Eukleidovské roviny působí tato Möbiova transformace dilaci od počátku souřadnicového systému.
Spinorové zobrazení ji konvertuje na Lorentzovu transformaci
Tento transformace reprezentuje boost podél osy z s Rapidita η. Jednoparametrická podgrupa, kterou generuje, lze získat nahrazením konstanty η reálnou proměnnou. Odpovídající spojité transformace nebeské sféry (až na identitu) vesměs sdílejí stejné pevné body (severní a jižní pól) a přesunují všechny jiné body podél zeměpisných délek od jižního pólu k severnímu.
Loxodromické transformace
Loxodromický prvek SL(2,C) je
a má pevné body ξ = 0, ∞. Spinorové zobrazení konvertuje toto na Lorentzovu transformaci
Jednoparametrický podgrupa toto generuje je získaný nahrazením η+iθ s jakýkoli reálný více tohoto komplexní konstanta. (Pokud η, θ se mění nezávisle, pak získáme dvourozměrné abelovské podgrupy sestávající ze současné rotace kolem osy z a boosty podél osy z; naproti tomu jednorozměrná podgrupa zde diskutovaná sestává z těch prvků této dvourozměrné podgrupy tak, že rychlost boostu a úhel rotace mají pevný poměr.)
Odpovídající spojité transformace nebeské sféry (až na identitu) vesměs sdílejí stejné dva pevné body (severní a jižní pól). Ty přesunují všechny ostatní body od jižního pólu a k severnímu pól (nebo naopak), podél rodiny křivek nazývané loxodromy. Každá loxodroma ovíjí nekonečně mnohokrát oba póly.
Parabolické transformace
Parabolický prvek grupy SL(2,C) je
a má na Riemannově sféře jediný pevný bod ξ = ∞. Při stereografické projekci se to projevuje jako obyčejné posunutí podél reálné osy.
Spinorové zobrazení konvertuje toto na matici (reprezentující Lorentzovu transformaci)
To generuje dvouparametrickou abelovskou podgrupu, kterou lze získat nahrazením konstanty α komplexní proměnnou. Odpovídající spojité transformace nebeské sféry (až na identickou transformaci) přesunují body podél rodina kružnic, které jsou vesměs tečné k severnímu pólu, na určitou hlavní kružnici. Všechny body různé od severního pólu samotného se přesunují podél těchto kružnic.
Parabolické Lorentzovy transformace se často nazývají nulové rotace. Protože jde pravděpodobně o nejméně známé ze čtyř typů neidentických Lorentzových transformací (eliptické, hyperbolické, loxodromické, parabolické), ukážeme zde, jak určit vliv příkladu parabolické Lorentzovy transformace na prostoročas Minkowského.
Výše uvedená matice dává transformaci
Bez ztráty obecnosti nyní položíme Im(α) = 0. Derivováním této transformace podle nyní reálného grupového parametru α a její vyhodnocení pro α=0 dává odpovídající vektorové pole (lineární parciální diferenciální operátor prvního řádu):
Nyní aplikujeme tento vztah na funkci f(t, x, y, z) a uplatníme požadavek, aby byla zachována invariance, tj. aby byla touto transformací anihilována. Řešení výsledné lineární parciální diferenciální rovnice prvního řádu lze vyjádřit ve tvaru
kde F je libovolná hladká funkce. Její argumenty dávají tři racionální invarianty popisující, jak se body (události) posunují při této parabolické transformaci, když se ony samy nepřesunují,
Volba reálných hodnot pro konstanty na pravé straně dává tři podmínky, která definují nějakou křivku v prostoročasu Minkowského. Tato křivka je orbitou transformace.
Tvar racionálních invariantů ukazuje, že popis těchto proudnic (orbit) je jednoduchý: zanedbáním neesenciální souřadnice y bude každá orbita průnikem nulové roviny, t = z + c2, s hyperboloidem, t2 − x2 − z2 = c3. Pro případ c3 = 0 hyperboloid degeneruje na světelný kužel a orbity přejdou na paraboly ležící v odpovídajících nulových rovinách.
Určitá nulová čára ležící na světelném kuželu je levým invariantem; to jednoznačně odpovídá (dvojitému) pevnému bodu na Riemannově sféře zmíněnému výše. Ostatní nulové čáry procházející počátkem souřadnicového systému jsou transformací „otočeny kolem kuželu“. Sledování pohybu jedné takové nulové čáry při zvětšujícím se α odpovídá sledování pohybu bodu podél jedné z kruhových linií toku na nebeské sféře, jak je popsáno výše.
Naopak volba Re(α) = 0 dává podobné orbity, ale s prohozenými rolemi x a y.
Parabolická transformace vede ke kalibrační symetrii nehmotných částic (jako jsou fotony) s helicitou |h| ≥ 1. Ve výše uvedeném explicitním příkladě není nehmotná částice pohybující se ve směru osy z, tedy se čtyřhybností P=(p, 0, 0, p), vůbec ovlivněna ani x-boostem ani y-rotační kombinací Kx − Jy definovanou níže v „malé grupě“ svého pohybu. To je zjevné z explicitní transformace tohoto zákona: jako jakýkoli světelný vektor je P samotný nyní invariantem, což znamená, že všechny stopy nebo účinky α zmizely. c1 = c2 = c3 = 0 ve zvláštním diskutovaném případě. (Jiný podobný generátor, Ky+Jx stejně jako on a Jz tvoří dohromady malou grupu světlupodobných vektorů, izomorfní s E(2).)
Vzhled noční oblohy
Tento izomorfismus má za následek, že Möbiovy transformace Riemannovy sféry představují způsob, jakým Lorentzovy transformace mění vzhled noční oblohy, jak ji vidí pozorovatel pohybující se relativistickými rychlostmi vůči „pevným hvězdám“.
Předpokládejme, že „pevné hvězdy“ se nacházejí v prostoročasu Minkowského a jsou znázorněny body na nebeské sféře. Pak lze každému bodu na nebeské sféře přiřadit komplexní číslo ξ = u + iv, které odpovídá určitému bodu na Riemannově sféře a lze jej identifikovat s nulovým vektorem (a světlupodobným vektorem) v prostoru Minkowského
nebo ve Weylově reprezentaci (spinorovém zobrazení) hermitovské matici
Množina reálných skalárních násobků tohoto nulového vektoru nazývaná nulová čára procházející počátkem souřadnicového systému reprezentuje přímou viditelnost různých vzdálených objektů, jako například hvězd, z místa pozorovatel v určitém místě a čase (libovolnou událost můžeme identifikovat s počátkem souřadnicového systému prostoročasu Minkowského). Pak body nebeské sféry (nebo ekvivalentně zorné čáry) lze identifikovat určitými hermitovskými maticemi.
Lieova algebra
Šablona:Lieovy grupy Jako u jakékoli Lieovy grupy je užitečným způsobem, jak studovat mnoho aspektů Lorentzovy grupy, její Lieova algebra. Protože Lorentzova grupa SO(1,3) je maticová Lieova grupa, její Lieova algebra so(1,3) je algebra matic, které lze počítat podle[5]
- .
Pokud je diagonální matice s diagonálními položkami , pak se Lieova algebra o(1,3) skládá z matic takových, že[6]
- .
Konkrétně so(1,3) se skládá z matic tvaru
- ,
kde jsou libovolná reálná čísla. Tato Lieova algebra je šestirozměrná. Podalgebra so(1,3) z prvků, v nichž se , a rovnají nule, je se so(3) izomorfní.
Pamatujte, že úplná Lorentzova grupa O(1,3), vlastní Lorentzova grupa SO(1,3) a vlastní ortochronní Lorentzova grupa všechny mají stejnou Lieovu algebru, která se typicky označuje so(1,3).
Protože komponenta identity Lorentzovy grupy je izomorfní s konečným kvocientem SL(2,C) (viz část výše o spojitosti Lorentzovy grupy s Möbiovou grupou), Lieova algebra Lorentzovy grupy je izomorfní s Lieovou algebrou sl(2,C). Pamatujte, že sl(2,C) je trojrozměrná, pokud je zobrazena jako komplexní Lieova algebra, ale šestirozměrná, pokud na ni pohlížíme jako na reálnou Lieovu algebru.
Generátory Möbiovy grupy
Další generující množina vznikne izomorfismem na Möbiově grupě. Následující tabulka udává šest generátorů, ve kterých
- První sloupec obsahuje generátor toku při Möbiově akci (po stereografické projekci z Riemannovy sféry) jako reálné vektorové pole v Eukleidovské rovině.
- Druhý sloupec obsahuje odpovídající jednoparametrickou podgrupu Möbiovy transformace.
- Třetí sloupec obsahuje odpovídající jednoparametrickou podgrupu Lorentzovy transformace (obraz při našem homomorfismu předchozí jednoparametrické podgrupy).
- Čtvrtý sloupec obsahuje odpovídající generátor toku při Lorentzově akci jako reálné vektorové pole na prostoročasu Minkowského.
Všimněte si, že generátory jsou následující
- Dva parabolické (nulové rotace)
- Jeden hyperbolický (boost ve směru ∂z)
- Tři eliptické (rotace postupně podle os x, y, z)
| Vektorové pole na R2 | Jednoparametrová podgrupa SL(2,C), reprezentující Möbiovy transformace |
Jednoparametrová podgrupa SO+(1,3), reprezentující Lorentzovy transformace |
Vektorové pole na R4 |
|---|---|---|---|
| Parabolické | |||
| Hyperbolické | |||
| Eliptické | |||
Verifujeme jeden řádek této tabulky. Začneme od
Uplatnění exponenciální funkce:
Tento prvek SL(2,C) reprezentuje jednoparametrickou podgrupu (eliptických) Möbiových transformací:
Nyní
Odpovídající vektorové pole na C (pohlížíme na něj jako na obraz S2 při stereografické projekci) je
Pokud vyjádříme , dostaneme vektorové pole na R2
Po návratu k našemu prvku SL(2,C), zapsáním akce a seskupením členů dostaneme, že obrazem spinorového zobrazení je prvek SO+(1,3)
Derivování podle θ v θ=0, dává odpovídající vektorové pole na R4,
To je zjevně generátor rotace proti směru hodinových ručiček kolem osy y.
Podgrupy Lorentzovy grupy
Až konjugace lze podalgebry Lieovy algebry Lorentzovy grupy vyčíslit, z topologických grup omezené Lorentzovy grupy lze vypsat, až konjugace. (Detaily jsou v knize od Halla citované níže.) To lze ihned vyjádřit pomocí generátorů daných ve výše uvedené tabulce.
Jednorozměrné podalgebry samozřejmě odpovídají čtyřem třídám konjugace prvků Lorentzovy grupy:
- generuje jednoparametrickou podalgebru parabol SO(0,1),
- generuje jednoparametrickou podalgebru boostů SO(1,1),
- generuje jednoparametrickou rotaci SO(2),
- (pro jakýkoli ) generuje jednoparametrickou podalgebru loxodromických transformací.
(Přesně řečeno, poslední odpovídá nekonečně mnoha třídám, protože různých dávají různé/jiný/odlišný třídy.) Dvourozměrný podalgebry jsou:
- generují abelovskou podalgebru sestávající výhradně z parabol,
- generují neabelovskou podalgebru izomorfní s Lieovou algebrou afinní grupy Aff(1),
- generují abelovskou podalgebru sestávající z boostů, rotací a loxodrom, které vesměs sdílejí stejný pár pevných bodů.
Trojrozměrný podalgebry používá Bianchiho klasifikační schéma:
- generují Bianchiho V podalgebru, izomorfní s Lieovou algebrou Hom(2), grupa eukleidovských homotheties,
- generují Bianchiho VII_0 podalgebru, izomorfní s Lieovou algebrou E(2), Eukleidova grupa,
- , kde , generují Bianchiho VII_a podalgebru,
- generují Bianchiho VIII podalgebru, izomorfní s Lieovou algebrou SL(2,R), grupa izometrií hyperbolické roviny,
- generují Bianchiho IX podalgebru, izomorfní s Lieovou algebrou SO(3), rotační grupa.
Bianchiho typy používají klasifikaci trojrozměrné Lieovy algebry italského matematika Luigiho Bianchiho. Čtyřrozměrné podalgebry jsou vesměs sdružený/konjugovaná funkce k
- generují podalgebru izomorfní s Lieovou algebrou Sim(2), grupa Eukleidovských podobností.
Podalgebry tvoří svazy (viz obrázek) a každá podalgebra generuje při použití exponenciální funkce topologické grupy omezené Lieovy grupy. Z toho plyne, že všechny podgrupy Lorentzovy grupy (až na konjugaci) lze zkonstruovat násobením jedním z prvků Kleinovy čtyřgrupy.
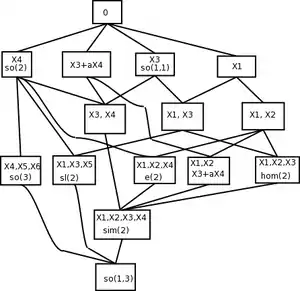
Jako u jakékoli souvislé Lieovy grupy, coset prostory uzavřené podgrupy omezené Lorentzovy grupy nebo homogenního prostoru mají významné matematické zájmy. Několik stručných popisů:
- Grupa Sim(2) je stabilizátor nulové line, tj. bodu na Riemannově sféře – tak homogenní prostor SO+(1,3)/Sim(2) je Kleinovské geometry, která reprezentuje konformní geometrii na kouli S2.
- (komponenta identity) Eukleidovská grupa SE(2) je stabilizátor nulový vektor, tak homogenní prostor SO+(1,3)/SE(2) je momentum prostor nehmotné částice; geometricky, toto Kleinovská geometrie reprezentuje degenerované geometrie světelného kužele v Minkowského prostoročasu.
- Rotační grupa SO(3) je stabilizátorem Minkowského prostoru, takže homogenní prostor SO+(1,3)/SO(3) je prostor hybnosti hmotné částice; geometricky tento prostor není nic jiného než trojrozměrný hyperbolický prostor H3.
Zobecnění na vyšší rozměry
Koncept Lorentzovy grupy má přirozené zobecnění na prostoročas s libovolným počtem rozměrů. Matematicky je Lorentzova grupa n+1-rozměrného prostoru Minkowského neurčitou ortogonální grupou O(n,1) lineární transformace Rn+1, která zachovává kvadratickou formu
Grupa O(1, n) zachovává kvadratickou formu
a je izomorfní s O(n,1) ale v matematické fyzice je oblíbenější, primárně protože algebra Diracovy rovnice a obecněji, spinorů a Cliffordových algeber, jsou s touto signaturou „přirozenější“.
Mnoho vlastností Lorentzovy grupy v čtyřrozměrném prostoru (kde n = 3) lze přímočaře zobecnit pro libovolné n. Například Lorentzova grupa O(n,1) má čtyři souvislé komponenty a působí konformními transformacemi na nebeskou (n−1)-koule v n+1-rozměrném Minkowského prostoru. Komponenta identity SO+(n,1) je SO(n)-bandl na hyperbolickém n-prostoru Hn.
Případy s nízkým počtem dimenzí n = 1 a n = 2 jsou často užitečné jako „hračkové modely“ pro fyzikální případ n = 3, zatímco Lorentzovy grupy s více rozměry se používají ve fyzikálních teoriích, například v teorii strun, která předpokládá existenci skrytých rozměrů. Lorentzova grupa O(n,1) je také grupa izometrií n-rozměrného De Sitterova prostoročasu dSn, která může být realizována homogenním prostorem O(n,1)/O(n−1,1). Konkrétně O(4,1) je grupa izometrií de Sitterova univerza dS4, což je kosmologický model.
Odkazy
Poznámky
- Explicitní odvození jsou v článku Weylova rovnice.
Reference
V tomto článku byl použit překlad textu z článku Lorentz group na anglické Wikipedii.
- Weinberg 2002.
- Varićak V 1910 „Teorie relativity a Lobačevského geometrie“,Phys Z 1910 §3 'Lorentz-Einstein transformace jako překlad/translace'. Engl.tr v Wikipedia
- Gelfand, Minlos a Shapiro 1963.
- Wigner 1939.
- Hall 2015 Definice 3.18
- Hall 2015 proposition 3.25
Literatura
- Artin, Emil, 1957. Geometric Algebra. New York: Wiley. ISBN 978-0-471-60839-4. Kapitola III popisuje ortogonální grupy O(p,q).
- Carmeli, Moshe, 1977. Group Theory and General Relativity, Representations of the Lorentz Group and Their Applications to the Gravitational Field. [s.l.]: McGraw-Hill, New York. ISBN 978-0-07-009986-9. Kanonické reference; kapitoly 1–6 popisují reprezentaci Lorentzovy grupy.
- Frankel, Theodore, 2004. The Geometry of Physics. 2. vyd. Cambridge: Cambridge University Press. ISBN 978-0-521-53927-2. Vynikající nástroj pro Lieovy teorie, fibrované bandly, spinorial pokrytí a mnoho jiných témat.
- Šablona:Fulton-Harris Lecture 11 pro ireducibilní reprezentace SL(2,C).
- GELFAND, I.M.; MINLOS, R.A.; SHAPIRO, Z.Ya., 1963. Representations of the Rotation and Lorentz Groups and their Applications. New York: Pergamon Press.
- HALL, Brian C., 2015. Lie Groups, Lie Algebras, and Representations: An Elementary Introduction. 2. vyd. [s.l.]: Springer. (Graduate Texts in Mathematics). ISBN 978-3319134666..
- Hall, G. S., 2004. Symmetries and Curvature Structure in General Relativity. Singapore: World Scientific. ISBN 978-981-02-1051-9. Kapitola 6 popisuje podalgebry Lieovy algebry Lorentzovy grupy.
- Hatcher, Allen, 2002. Algebraic topology. Cambridge: Cambridge University Press. ISBN 978-0-521-79540-1. Viz také online version [online]. [cit. 2005-07-03]. Dostupné online. Section 1.3 pěkně ilustruje diskuzi pokrývající prostory. Section 3D popisuje topologie rotační grupy.
- MISNER, Charles; THORNE, Kip S.; WHEELER, John, 1973. Gravitation. [s.l.]: W. H. Freeman and Company. ISBN 978-0-7167-0344-0. §41.3
- Naber, Gregory, 1992. The Geometry of Minkowski Spacetime. New York: Springer-Verlag. ISBN 978-0486432359. (Dover reprint vydání.) Vynikající reference na prostoročas Minkowského a Lorentzovy grupy.
- Needham, Tristan, 1997. Visual Complex Analysis. Oxford: Oxford University Press. ISBN 978-0-19-853446-4. Kapitola 3 pro skvělé znázornění diskuze Möbiovy transformace.
- WEINBERG, S., 2002. The Quantum Theory of Fields. [s.l.]: Cambridge University Press. Dostupné online. ISBN 978-0-521-55001-7.
- WIGNER, E. P., 1939. On unitary representations of the inhomogeneous Lorentz group. Annals of Mathematics. Roč. 40, čís. 1, s. 149–204. DOI 10.2307/1968551. JSTOR 1968551. Bibcode 1939AnMat..40..149W..
Související články
|
|