Fibrovaný prostor

Fibrovaný prostor (angl. fibre bundle) je definován jako uspořádaná čtveřice ${\displaystyle \scriptstyle (E,M,F,\pi )}$ následujících objektů:

1. ${\displaystyle E}$ je diferencovatelná varieta zvaná totální prostor,
2. ${\displaystyle M}$ je diferencovatelná varieta zvaná bázová varieta či báze,
3. ${\displaystyle F}$ je diferencovatelná varieta zvaná typické vlákno, nebo jen vlákno,
4. ${\displaystyle \pi :E\to M}$ je surjektivní zobrazení totálního prostoru na bázovou varietu, který se nazývá projekce.
5. Spolu s předchozími objekty je nutno zadat i otevřené pokrytí ${\displaystyle \scriptstyle \{U_{\alpha }\}_{\alpha \in I}}$ bázové variety ${\displaystyle \scriptstyle M}$ a jemu odpovídající množinu zobrazení ${\displaystyle \scriptstyle \{\varphi _{\alpha }\}_{\alpha \in I}}$, kde index ${\displaystyle \scriptstyle \alpha }$ probíhá (ne nutně konečnou či spočetnou) indexovou množinu ${\displaystyle \scriptstyle I}$. Platí tedy ${\displaystyle \scriptstyle \bigcup _{\alpha \in I}U_{\alpha }=M}$, kde ${\displaystyle \scriptstyle U_{\alpha }}$ jsou otevřené množiny. Dále, pro každé ${\displaystyle \scriptstyle \alpha }$ je zobrazení ${\displaystyle \scriptstyle \varphi _{\alpha }:U_{\alpha }\times F\to \pi ^{(-1)}(U_{\alpha })}$ difeomorfizmus splňující dodatečnou podmínku

${\displaystyle \pi (\varphi _{\alpha }(m,f))=m,\quad \forall m\in M}$,

kde symbolem ${\displaystyle \scriptstyle \pi ^{(-1)}(U_{\alpha })}$ značíme vzor množiny ${\displaystyle \scriptstyle U_{\alpha }}$ při zobrazení ${\displaystyle \scriptstyle \pi }$. Zobrazení ${\displaystyle \scriptstyle \varphi _{\alpha }}$ se nazývají lokální trivializace. (Někdy se za lokální trivializace berou zobrazení ${\displaystyle \scriptstyle {\tilde {\varphi }}_{\alpha }:\pi ^{(-1)}(U_{\alpha })\to U_{\alpha }\times F}$, která v podstatě odpovídají inverzím pro námi zavedené trivializace ${\displaystyle \scriptstyle \varphi _{\alpha }}$. Neboť jsou lokální trivializace bijekce, tak vztah zobrazení a jeho inverze je jednoznačný a oba přístupy jsou tak ekvivalentní.)

Fibrovaný prostor ${\displaystyle \scriptstyle (E,M,F,\pi )}$ se často značí jen jako ${\displaystyle \scriptstyle E}$ nebo výrazem

${\displaystyle E\ {\stackrel {\pi }{\rightarrow }}\ M}$.

Přísně vzato, definice fibrovaného prostoru by měla být nezávislá na konkrétní volbě otevřeného pokrytí ${\displaystyle \scriptstyle \{U_{\alpha }\}_{\alpha }}$. Matematicky korektně se tedy postupuje tak, že se nejdříve definicí výše zavádějí souřadnicové fibrované prostory [pozn. 1] ${\displaystyle \scriptstyle (E,M,F,\pi ,\{U_{\alpha }\}_{\alpha \in I},\{\varphi _{\alpha }\}_{\alpha \in I})}$. Na množině všech takovýchto souřadnicových fibrovaných prostorů s různými pokrytími se zadefinuje relace ekvivalence tak, že ${\displaystyle \scriptstyle (E,M,F,\pi ,\{U_{\alpha }\}_{\alpha \in I},\{\varphi _{\alpha }\}_{\alpha \in I})}$ je ekvivalentní s ${\displaystyle \scriptstyle (E,M,F,\pi ,\{V_{\beta }\}_{\beta \in J},\{\varphi _{\beta }\}_{\beta \in J})}$ právě tehdy, když ${\displaystyle \scriptstyle (E,M,F,\pi ,\{U_{\alpha }\}_{\alpha \in I}\cup \{V_{\beta }\}_{\beta \in J},\{\varphi _{\alpha }\}_{\alpha \in I}\cup \{\varphi _{\beta }\}_{\beta \in J})}$ je opět souřadnicovým fibrovaným prostorem. Množinu všech souřadnicových fibrovaných prostorů si tedy můžeme faktorizovat podle této ekvivalence a fibrovaný prostor samotný je pak definován jako třída ekvivalence v tomto faktorprostoru. [1]

Okolí ${\displaystyle \scriptstyle \{U_{\alpha }\}_{\alpha }}$ pokrývají bázovou varietu ${\displaystyle \scriptstyle M}$. Ke každému ${\displaystyle \scriptstyle U_{\alpha }}$ je přitom přiřazena lokální trivializace ${\displaystyle \scriptstyle \varphi _{\alpha }}$. Na průniku dvou okolí ${\displaystyle \scriptstyle U_{\alpha }\cap U_{\beta }}$ tak máme bod ${\displaystyle \scriptstyle p\in E}$ totálního prostoru vyjádřen pomocí dvou různých trivializací

${\displaystyle p=\varphi _{\alpha }(m,f_{\alpha })=\varphi _{\beta }(m,f_{\beta }),}$

kde ${\displaystyle \scriptstyle m\in M}$ je takové, že platí ${\displaystyle \scriptstyle \pi (p)=m}$. Skutečnost, že v obou případech máme stejné ${\displaystyle \scriptstyle m\in M}$ pro obě trivializace vyplývá z požadavku kladeného na tato zobrazení v definici fibrovaného prostoru. Co je obecně různé jsou však prvky ${\displaystyle \scriptstyle f_{\alpha },f_{\beta }\in F}$. Můžeme si tak zavést zobrazení ${\displaystyle \scriptstyle \tau _{\alpha \beta }^{(m)}:F\to F}$ předpisem

${\displaystyle \tau _{\alpha \beta }^{(m)}(f_{\alpha })=f_{\beta }}$.

Takto zavedeným zobrazením se říká přechodové funkce. Konvence pro jejich značení se liší u různých autorů. Místo označení ${\displaystyle \scriptstyle \tau _{\alpha \beta }}$ se tak lze setkat i s opačným pořadím indexů ${\displaystyle \scriptstyle \tau _{\beta \alpha }}$ apod. Přechodové funkce se mají k lokálním trivializacím způsobem

${\displaystyle (\varphi _{\beta }^{-1}\circ \varphi _{\alpha })(m,f)=(m,\tau _{\alpha \beta }^{(m)}f),\quad \forall m\in M,\ \forall f\in F}$.

Pokud ${\displaystyle \scriptstyle \alpha =\beta }$, je odpovídající přechodová funkce ${\displaystyle \scriptstyle \tau _{\alpha \alpha }}$ zjevně rovna identitě. Dále, pokud platí ${\displaystyle \scriptstyle \tau _{\alpha \beta }(f_{\alpha })=f_{\beta }}$, tak zřejmě i ${\displaystyle \scriptstyle \tau _{\beta \alpha }(f_{\beta })=f_{\alpha }}$, z čehož vyplývá ${\displaystyle \scriptstyle \tau _{\alpha \beta }^{-1}=\tau _{\beta \alpha }}$. Pokud bychom neuvažovali pouze body z průniku dvou okolí ${\displaystyle \scriptstyle U_{\alpha }\cap U_{\beta }\subset M}$, ale rovnou ze tří okolí ${\displaystyle \scriptstyle U_{\alpha }\cap U_{\beta }\cap U_{\gamma }\subset M}$, tak bychom podobnými úvahami dospěli i ke vztahu

${\displaystyle \tau _{\alpha \gamma }=\tau _{\beta \gamma }\circ \tau _{\alpha \beta }}$.

Ukázali jsme tak, že v množině všech přechodových zobrazení ${\displaystyle \scriptstyle \{\tau _{\alpha \beta }\}_{\alpha ,\beta }}$ se nachází jednotkový prvek (identické zobrazení), každý prvek má k sobě inverzní prvek a že tato množina je uzavřená vůči operaci skládání prvků coby zobrazení. Skládání zobrazení je asociativní a tyto všechny vlastnosti nám tedy říkají, že množina všech přechodových zobrazení (spolu s operací skládání zobrazení) tvoří grupu. Této grupě se říká strukturní grupa. V našem postupu jsme měli zadány lokální trivializace a z nich jsme sestrojili přechodové funkce. Lze se však vydat i opačným směrem, kdy máme předem zadané přechodové funkce a z nich jsme schopni zrekonstruovat lokální trivializace, viz oddíl Rekonstrukce fibrovaného prostoru ze znalosti přechodových zobrazení níže. Strukturní grupa se tedy někdy vyskytuje v samotné definici fibrovaného prostoru.

• Vzor jednobodové množiny ${\displaystyle \scriptstyle \{m\}}$ při zobrazení ${\displaystyle \scriptstyle \pi }$, tj. ${\displaystyle \scriptstyle \pi ^{(-1)}(\{m\})\subset E}$ pro daný bod ${\displaystyle \scriptstyle m\in M}$ bázové variety, nazýváme vlákno nad bodem m. Množina ${\displaystyle \scriptstyle \pi ^{(-1)}(\{m\})}$ je diferencovatelná varieta izomorfní typickému vláknu ${\displaystyle \scriptstyle F}$.

• Jako řez, resp. řez fibrovaného prostoru, označujeme hladké zobrazení ${\displaystyle \scriptstyle \sigma :M\to E}$ vyhovující podmínce ${\displaystyle \scriptstyle \pi \circ \sigma =\mathrm {Id} }$, kde ${\displaystyle \scriptstyle \mathrm {Id} }$ označuje identitu na bázové varietě. Právě uvedenou podmínku lze přepsat do tvaru

${\displaystyle \pi (\sigma (m))=m,\quad \forall m\in M}$.

Množina všech řezů na prostoru ${\displaystyle \scriptstyle E}$ se často značí symbolem ${\displaystyle \scriptstyle \Gamma (E)}$. Podobně, jako lokální řez (na okolí ${\displaystyle \scriptstyle U}$) označíme hladké zobrazení ${\displaystyle \scriptstyle \sigma :U\to E}$ vyhovující podmínce ${\displaystyle \scriptstyle \pi \circ \sigma =\mathrm {Id} |_{U}}$, kde ${\displaystyle \scriptstyle U\subset M}$ je otevřená podmnožina bázové variety. Důvod, proč se řezy nazývají právě „řezy“, je ten, že zobrazení ${\displaystyle \scriptstyle \sigma }$ vybere pro daný bod ${\displaystyle \scriptstyle m\in M}$ bázové variety jen jeden bod ${\displaystyle \scriptstyle p\in E}$ z vlákna nad bodem ${\displaystyle \scriptstyle m}$. Pro libovolné další ${\displaystyle \scriptstyle m'\in M}$ se už nemůže stát, že by ${\displaystyle \scriptstyle \sigma (m')}$ spadlo do téhož vlákna. Situace je lépe nahlédnutelná na animovaném Obr. 2 níže. V tomto případě je řezem hladké zobrazení ${\displaystyle \scriptstyle \sigma }$, které bere body kružnice a vrací body v Möbiově pásce. Na obrázku je v Möbiově pásce vyznačen větší počet typických vláken, v tomto případě představovaných úsečkami. Celá úsečka přitom odpovídá jedinému bodu kružnice. Řez ${\displaystyle \scriptstyle \sigma }$ bere po řadě body kružnice a každému takovému bodu přiřazuje jen jeden bod na odpovídající úsečce.

• Zobrazením fibrovaných prostorů ${\displaystyle \scriptstyle (E,M,F,\pi )}$ a ${\displaystyle \scriptstyle (E',M',F',\pi ')}$ nazýváme dvojici zobrazení ${\displaystyle \scriptstyle \phi :E\to E'}$ a ${\displaystyle \scriptstyle \psi :M\to M'}$ splňující podmínku

${\displaystyle \pi '\circ \phi =\psi \circ \pi }$.

• Mějme fibrovaný prostor ${\displaystyle \scriptstyle (E,M,F,\pi )}$. Pokud existuje vzájemně jednoznačné zobrazení fibrovaných prostorů ${\displaystyle \scriptstyle (E,M,F,\pi )}$ a ${\displaystyle \scriptstyle (M\times F,M,F,\pi ')}$, (kde ${\displaystyle \scriptstyle \pi '((m,f))=m}$) tak říkáme, že fibrovaný prostor ${\displaystyle \scriptstyle (E,M,F,\pi )}$ je triviální. Tehdy je ${\displaystyle \scriptstyle (E,M,F,\pi )}$ v podstatě pouze kartézským součinem ${\displaystyle \scriptstyle M\times F}$.

• Dva fibrované prostory ${\displaystyle \scriptstyle (E,M,F,\pi )}$ a ${\displaystyle \scriptstyle (E',M',F',\pi ')}$ jsou ekvivalentní, existuje-li zobrazení fibrovaných prostorů ${\displaystyle \scriptstyle (\phi ,\psi )}$ tak, že ${\displaystyle \scriptstyle \psi :M\to M'}$ je identické zobrazení a ${\displaystyle \scriptstyle \phi :E\to E'}$ je difeomorfizmus.

Jak již bylo řečeno, fibrovaný prostor má do jisté míry zobecňovat pojem kartézského součinu. Popravdě řečeno, kartézský součin dvou diferencovatelných variet ${\displaystyle \scriptstyle A\times B}$ lze chápat jako jednoduchý fibrovaný prostor ${\displaystyle \scriptstyle (A\times B,B,A,\pi )}$, kde ${\displaystyle \scriptstyle A\times B}$ je nyní totální prostor, ${\displaystyle \scriptstyle B}$ je bázová varieta a ${\displaystyle \scriptstyle A}$ je typické vlákno. Projekci ${\displaystyle \scriptstyle \pi }$ si v tomto případě můžeme definovat způsobem ${\displaystyle \scriptstyle \pi ((a,b))=b}$, pro libovolné ${\displaystyle \scriptstyle a\in A}$, ${\displaystyle \scriptstyle b\in B}$. Pokud si dále vezmeme nějaké otevřené pokrytí ${\displaystyle \scriptstyle \{U_{\alpha }\}_{\alpha }}$ variety ${\displaystyle \scriptstyle B}$, tak ke každému okolí ${\displaystyle \scriptstyle U_{\alpha }}$ můžeme definovat lokální trivializaci ${\displaystyle \scriptstyle \varphi _{\alpha }(a,b)=(a,b)}$, která ze dvou bodů vytvoří jejich uspořádanou dvojici. Máme tak všechny suroviny vystupující v definici fibrovaného prostoru a můžeme uzavřít, že kartézský součin je skutečně triviálním případem fibrovaného prostoru.

Nezůstaňme ovšem jen u triviálních případů. Každý fibrovaný prostor, resp. jeho totální prostor, totiž jako kartézský součin vypadá alespoň lokálně. Zhruba řečeno je ke každému bodu bázové variety ${\displaystyle \scriptstyle M}$ přilepena jiná varieta, vlákno ${\displaystyle \scriptstyle F}$. Ostatně samotné lokální trivializace ${\displaystyle \scriptstyle \varphi _{\alpha }}$, jak již jejich název dává tušit, slouží k lokálnímu převodu totálního prostoru na kartézský součin dvou množin. Pro každé okolí ${\displaystyle \scriptstyle U_{\alpha }}$ lze množinu ${\displaystyle \scriptstyle V_{\alpha }=\pi ^{(-1)}(U_{\alpha })}$ (která je podmnožinou totálního prostoru ${\displaystyle \scriptstyle E}$) zobrazit díky ${\displaystyle \scriptstyle \varphi _{\alpha }^{-1}}$ difeomorfně na kartézský součin okolí a vlákna, tj.

${\displaystyle \varphi _{\alpha }^{-1}:V_{\alpha }\to U_{\alpha }\times F}$.

Jedním z nejjednodušších příkladů fibrovaných prostorů, které nelze vyjádřit jako kartézský součin, je Möbiova páska, na níž lze pěkně ilustrovat role jednotlivých objektů vystupujících v definici fibrovaného prostoru. Celá situace je znázorněna na obr. 1 níže. Na tomto obrázku vidíme následující:

1. červenou barvou je vyobrazen totální prostor E, tedy v tomto případě Möbiova páska,
2. zelenou barvou je vykreslena bázová varieta M, která je v našem případě obyčejnou kružnicí,
3. modrou barvou je zachyceno typické vlákno F; v našem případě se jedná o úsečku.

Na bázové varietě, kružnici, jsou dále pro názornost vybrány tři různé body ${\displaystyle \scriptstyle m_{1},m_{2},m_{3}}$. Vzory těchto bodů při projekci ${\displaystyle \scriptstyle \pi }$ jsou po řadě vlákna ${\displaystyle \scriptstyle F_{1},F_{2},F_{3}}$. Vlákno nad bodem ${\displaystyle \scriptstyle m_{1}}$ je tedy označeno ${\displaystyle \scriptstyle F_{1}}$ a podobně pro ostatní body. Vidíme tak, že jednomu bodu kružnice odpovídá celá úsečka bodů na Möbiově pásce. Každá z těchto úseček je v podstatě rovna typickému vláknu ${\displaystyle \scriptstyle F}$. Jednotlivé body na dané úsečce lze pak rozlišit pomocí bodů z typického vlákna, kterážto situace je znázorněna pro případ bodu ${\displaystyle \scriptstyle p_{3}\in E}$. Jeho projekce na bázovou varietu je ${\displaystyle \scriptstyle m_{3}}$ a v rámci vlákna ${\displaystyle \scriptstyle F_{3}}$ je ${\displaystyle \scriptstyle p_{3}}$ jednoznačně identifikován bodem ${\displaystyle \scriptstyle f_{3}\in F}$. Nějakému jinému prvku ${\displaystyle \scriptstyle p_{4}}$ ze stejného vlákna ${\displaystyle \scriptstyle F_{3}}$ by odpovídal jiný bod ${\displaystyle \scriptstyle f_{4}\in F_{3}}$, ačkoli jeho projekce ${\displaystyle \scriptstyle \pi (p_{4})}$ by byla stále rovna ${\displaystyle \scriptstyle m_{3}\in M}$, tj. ${\displaystyle \scriptstyle \pi (p_{4})=m_{3}}$.

• 
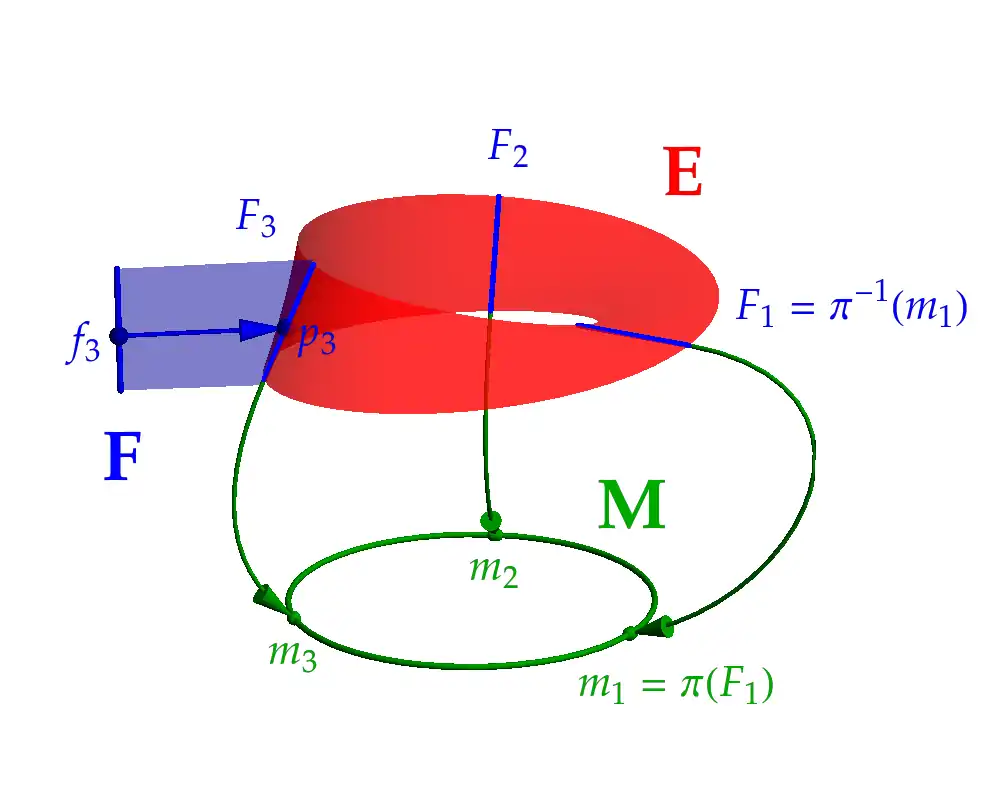  Obr. 1: Möbiova páska coby fibrovaný prostor. Möbiova páska samotná představuje totální prostor E. Bázovou varietou M je kružnice a typickým vláknem F je úsečka. Explicitně jsou vyobrazeny tři body na kružnici a jim odpovídající vlákna na Möbiově pásce. Bod ${\displaystyle \scriptstyle p_{3}}$ na pásce je parametrizován jednak svou projekcí ${\displaystyle \scriptstyle m_{3}}$, jednak prvkem vlákna ${\displaystyle \scriptstyle f_{3}}$.
• 
  Obr. 2: Möbiovu pásku lze obdržet jako kružnici, po níž přecházíme úsečkou, kterou postupně stáčíme aby při oběhnutí kružnice hladce nasedla na svou původní, výchozí, polohu. V animaci jsou zobrazena modrou barvou vlákna nad některými body kružnice.

Způsob, jakým se došlo od Möbiově pásce ke kružnici, coby bázové varietě, s úsečkou, coby vláknem, je naznačen v animaci na Obr. 2 a podrobněji matematicky rozebrán v následujícím. Möbiova páska je dvourozměrná varieta, kterou můžeme vložit do trojrozměrného prostoru ${\displaystyle \scriptstyle \mathbb {R} ^{3}}$ a na jejíž body se pak díky tomu můžeme odkazovat pomocí jejich souřadnic ${\displaystyle \scriptstyle (x,y,z)}$. Parametrické rovnice Möbiovy křivky o jednotkovém poloměru a jednotkové šířce v těchto souřadnicích potom znějí

${\displaystyle {\begin{array}{rcl}x(u,v)&=&(1+u\cos({\frac {v}{2}}))\cos(v),\\y(u,v)&=&(1+u\cos({\frac {v}{2}}))\sin(v),\\z(u,v)&=&u\,\sin({\frac {v}{2}}),\end{array}}}$

kde ${\displaystyle \scriptstyle u\in [-1/2,1/2]}$ a ${\displaystyle \scriptstyle v\in [0,2\pi )}$. Od teď nebudeme rozlišovat mezi Möbiovou páskou a jejím vložením do ${\displaystyle \scriptstyle \mathbb {R} ^{3}}$. Pod bodem Möbiovy pásky tak budeme rozumět trojici čísel ${\displaystyle \scriptstyle (x,y,z)}$ vyhovující parametrickým rovnicím výše.

Položíme-li ${\displaystyle \scriptstyle u=0}$ pevně, tak okamžitě vidíme, že křivka ${\displaystyle \scriptstyle \{(x(0,v),y(0,v),z(0,v))|v\in [0,2\pi )\}}$ je jednotková kružnice ležící ve vodorovné rovině, neboť platí

${\displaystyle (x(0,v))^{2}+(y(0,v))^{2}=1,\quad z(0,v)=0,\quad \forall v\in [0,2\pi )}$.

Za bázovou varietu si tedy skutečně můžeme vzít jednotkovou kružnici, která je parametrizovaná proměnnou ${\displaystyle \scriptstyle v}$. Máme-li na kružnici ${\displaystyle \scriptstyle M}$ zvolen pevně jistý počáteční bod, tak mu můžeme přiřadit hodnotu ${\displaystyle \scriptstyle v=0}$. Pokud zvětšujeme parametr ${\displaystyle \scriptstyle v}$ postupně od nuly do ${\displaystyle \scriptstyle 2\pi }$, tak projdeme všechny body kružnice. Každému bodu ${\displaystyle \scriptstyle m_{0}\in M}$ kružnice je tak jednoznačně přiřazeno jisté číslo ${\displaystyle \scriptstyle v_{0}\in [0,2\pi )}$. Tento vztah budeme v tomto oddíle vyjadřovat zápisem ${\displaystyle \scriptstyle m_{0}=m(v_{0})}$. Kružnice je jednorozměrná křivka a pokud ji vnoříme do trojrozměrného prostoru ${\displaystyle \scriptstyle \mathbb {R} ^{3}}$, tak jí můžeme ztotožnit s množinou ${\displaystyle \scriptstyle \{(x(0,v),y(0,v),z(0,v))|v\in [0,2\pi )\}}$. V takovém případě má počáteční bod kružnice souřadnice ${\displaystyle \scriptstyle \{(x(0,0),y(0,0),z(0,0))\}}$ a souřadnice ${\displaystyle \scriptstyle (x(v),y(v),z(v))}$ bodu ${\displaystyle \scriptstyle m(v)}$ mají tvar

${\displaystyle x(v)=\cos(v),\quad y(v)=\sin(v),\quad z(v)=0}$.

Jestliže si nyní ukotvíme parametr ${\displaystyle \scriptstyle v}$ a položíme ho rovno číslu ${\displaystyle \scriptstyle v_{0}=konst.}$, tak lze parametrické rovnice Möbiovy křivky přepsat do tvaru

${\displaystyle {\begin{array}{rcl}x(u)&=&\cos(v_{0})+u\,(\cos({\frac {v_{0}}{2}})\cos(v_{0})),\\y(u)&=&\sin(v_{0})+u\,(\cos({\frac {v_{0}}{2}})\sin(v_{0})),\\z(u)&=&u\,\sin({\frac {v_{0}}{2}}),\end{array}}}$

což je parametrické vyjádření úsečky ve trojrozměrném prostoru (parametr ${\displaystyle \scriptstyle u}$ probíhá omezený interval od −1/2 do 1/2). Proměnná ${\displaystyle \scriptstyle u}$ tedy parametrizuje vlákno; udává „vzdálenost“ bodu úsečky od jejího středu. Zaveďme pro prvky vlákna podobné značení, jaké jsme přijali pro prvky bázové variety. Konkrétně bod ${\displaystyle \scriptstyle f_{0}}$ ve „vzdálenosti“ ${\displaystyle \scriptstyle u_{0}}$ od středu úsečky vyjadřujme vztahem ${\displaystyle \scriptstyle f_{0}=f(u_{0})}$.

Uvažujme nyní nějaký konkrétní bod Möbiovy pásky, např. bod ${\displaystyle \scriptstyle p_{3}}$ na Obr. 1. Nechť jeho souřadnice znějí ${\displaystyle \scriptstyle (x(u_{3},v_{3}),y(u_{3},v_{3}),z(u_{3},v_{3}))}$ pro nějaké ${\displaystyle \scriptstyle u_{3}}$ a ${\displaystyle \scriptstyle v_{3}}$. Za projekci tohoto bodu na bázovou varietu položíme bod na kružnici, jehož vzdálenost od počátečního bodu kružnice je rovna ${\displaystyle \scriptstyle v_{3}}$. Pokud si za počáteční bod kružnice zvolíme bod ${\displaystyle \scriptstyle m_{1}}$ na Obr. 1, pro nějž platí ${\displaystyle \scriptstyle m_{1}=m(0)}$, tak projekcí bodu ${\displaystyle \scriptstyle p_{3}}$ je bod ${\displaystyle \scriptstyle m_{3}=m(v_{3})}$. V návaznosti na tento postup si tak zavedeme projekci ${\displaystyle \scriptstyle \pi :E\to M}$ vztahem

${\displaystyle \pi ((x(u,v),y(u,v),z(u,v)))=m(v),\quad \forall u\in [-1/2,1/2],\quad \forall v\in [0,2\pi )}$.

Projekce nám tak smaže veškerou informaci o vlákně skrytou v proměnné ${\displaystyle \scriptstyle u}$.

Zbývá nám určit lokální trivializace, jež sestávají z okolí pokrývajících bázovou varietu a k nim přiřazených zobrazení splňujících dodatečné podmínky. Za pokrytí kružnice bychom si mohli zvolit dvojici okolí

${\displaystyle U_{1}=\{m\in M|m=m(v),v\in (0,\,5)\},\quad U_{2}=\{m\in M|m=m(v),v\in \left(5-{\frac {1}{10}},\,2\pi +{\frac {1}{10}}\right)\}}$.

Pokud bychom uvažovali bázovou varietu ${\displaystyle \scriptstyle M}$ coby kružnici vloženou do ${\displaystyle \scriptstyle \mathbb {R} ^{3}}$, tak by šlo vyjádřit tato okolí ve tvaru

${\displaystyle U_{1}=\{(\cos(v),\sin(v),0)|v\in (0,\,5)\},\quad U_{2}=\{(\cos(v),\sin(v),0)|v\in \left(5-{\frac {1}{10}},\,2\pi +{\frac {1}{10}}\right)\}}$.

Meze intervalů jsme zvolili více méně libovolně, důležité je, aby tyto intervaly byly otevřené a jejich sjednocení bylo nadmnožinou intervalu ${\displaystyle \scriptstyle (0,2\pi )}$. Okolí bychom si mohli zvolit i více, rozhodně ne však méně. Později si ukážeme, že jediné okolí pokrývající kružnici M nelze pro zavedení lokálních trivializací použít. Pro aktuální volbu okolí nyní stačí za lokální trivializace vzít zobrazení ${\displaystyle \scriptstyle \varphi _{1}:U_{1}\times F\to \pi ^{(-1)}(U_{1})}$, ${\displaystyle \scriptstyle \varphi _{2}:U_{2}\times F\to \pi ^{(-1)}(U_{2})}$, jejichž předpis v parametrizaci pomocí proměnných ${\displaystyle \scriptstyle u,v}$ zní

${\displaystyle \varphi _{1}(m,f)=(x(u,v),y(u,v),z(u,v)),\quad {\text{kde}}\quad m=m(v),\ f=f(u),\quad \forall u\in [-1/2,\,1/2],\ \forall v\in [0,\,5)}$.

${\displaystyle \varphi _{2}(m,f)=(x(u,v),y(u,v),z(u,v)),\quad {\text{kde}}\quad m=m(v),\ f=f(u),\quad \forall u\in [-1/2,\,1/2],\ \forall v\in [5-1/10,2\pi +1/10)}$.

Parametrické rovnice Möbiovy pásky jsou tedy v podstatě lokálními trivializacemi. Zobrazení ${\displaystyle \scriptstyle \varphi _{1}}$ vezme jednak bod kružnice ${\displaystyle \scriptstyle m=m(v)}$ parametrizovaný hodnotou ${\displaystyle \scriptstyle v\in (0,5)}$, jednak bod typického vlákna ${\displaystyle \scriptstyle f=f(u)}$ parametrizovaný hodnotou ${\displaystyle \scriptstyle u\in [-1/2,1/2]}$, a této dvojici prvků přiřadí bod Möbiovy pásky, jehož souřadnice ${\displaystyle \scriptstyle (x(u,v),y(u,v),z(u,v))}$ se získají z parametrických rovnic. Trivializace ${\displaystyle \scriptstyle \varphi _{2}:U_{2}\times F\to \pi ^{(-1)}(U_{2})}$ se chová podobně, akorát její definiční obor je omezen na hodnoty ${\displaystyle \scriptstyle u\in [-1/2,1/2]}$ a ${\displaystyle \scriptstyle v\in (5-1/10,2\pi +1/10)}$. Pro názornost jsou pokrývající okolí i působení lokálních trivializací vykreslena na Obr. 3.

Zodpovězme nyní otázku, proč jsme uvážili dvě okolí ${\displaystyle \scriptstyle U_{1},U_{2}}$ namísto jednoho ${\displaystyle \scriptstyle U}$, které by pokrylo celou kružnici a které by mělo tvar

${\displaystyle U=\{m\in M|m=m(v),v\in [0,2\pi )\}=M}$.

Množina ${\displaystyle \scriptstyle U}$ je zjevně pokrývající a otevřená (celá množina vždy patří do své topologie a splňuje tak podmínku otevřenosti). Co nám tedy brání ji použít? Potíž je v tom, že odpovídající lokální trivializace ${\displaystyle \scriptstyle \varphi }$ by nebyla na celém svém definičním oboru hladké zobrazení. Abychom toto nahlédli mějme analogicky předchozímu případu

${\displaystyle \varphi (m,f)=(x(u,v),y(u,v),z(u,v)),\quad {\text{kde}}\quad m=m(v),\ f=f(u),\quad \forall u\in [-1/2,1/2],\ \forall v\in [0,2\pi )}$.

Při obejití kružnice se dostaneme zpět na počátek a musí tedy platit, že hodnoty lokální trivializace pro ${\displaystyle \scriptstyle v=0}$ a ${\displaystyle \scriptstyle v=2\pi }$ se při ukotveném ${\displaystyle \scriptstyle u=u_{0}=konst.}$ rovnají. Hodnota ${\displaystyle \scriptstyle 2\pi }$ přísně vzato neleží v definičním oboru a tato podmínka proto zní

${\displaystyle \varphi (m(0),f(u_{0}))=\lim _{v\to 2\pi _{-}}\varphi (m(v),f(u_{0}))}$.

Položíme-li ${\displaystyle \scriptstyle u_{0}=1/2}$, tak se levá strana redukuje do tvaru ${\displaystyle \scriptstyle \varphi (m(0),f(1/2))=(1.5,0,0)}$, zatímco pravá strana přechází na tvar ${\displaystyle \scriptstyle (0.5,0,0)}$. Rovnost tedy viditelně nenastává a s jediným pokrývajícím okolím Möbiovy pásky si tak nevystačíme. Graficky lze nespojitost zobrazení ${\displaystyle \scriptstyle \varphi :M\times F\to E}$ vidět na animaci v Obr. 2, kde šipka „generující“ pásku na počátku směřuje ven, při oběhnutí kružnice však směřuje dovnitř pomyslného kruhu.

Naše volba dvou okolí s danými trivializacemi problém nespojitosti zobrazení obchází. Zatímco u jednoho okolí ${\displaystyle \scriptstyle U=M}$ mělo toto topologii kruhu a daná trivializace musela být „spojitá v počátečním bodě“, tak pokud použijeme okolí dvě, tak každé z nich má topologii úsečky (bez koncových bodů) a o žádnou spojitost v „počátečním bodě“ se nemusíme starat.

• 
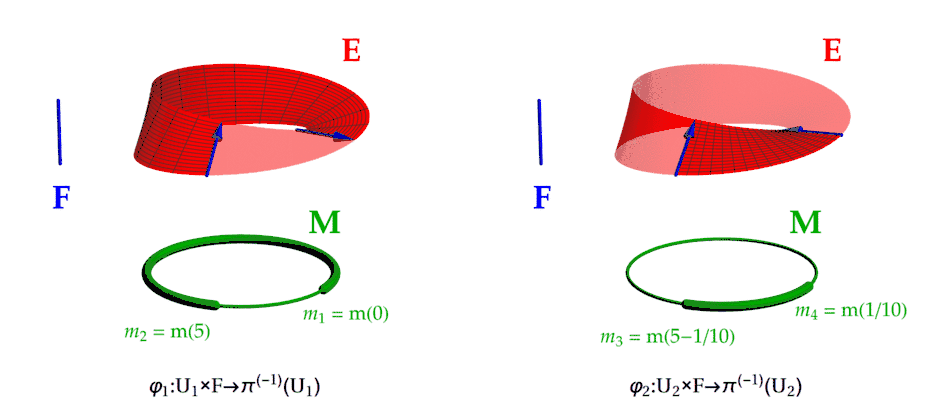  Obr. 3: Möbiova páska spolu s lokálními trivializacemi. Vlevo je zobrazeno okolí ${\displaystyle \scriptstyle U_{1}}$ bázové variety ${\displaystyle \scriptstyle M}$ coby tlustší úsek kružnice ohraničený body ${\displaystyle \scriptstyle m_{1}}$ a ${\displaystyle \scriptstyle m_{2}}$. Odpovídající kus Möbiovy pásky, který je zobrazen na toto okolí a vlákno pomocí lokální trivializace ${\displaystyle \scriptstyle \varphi _{1}}$, je pak vyobrazen sytou barvou. Trivializace přitom působí takovým způsobem, že daný úsek pásky je zobrazen na "obdélník" ${\displaystyle \scriptstyle U_{1}\times F}$. Mřížka pokrývající daný úsek Möbiovy pásky je tak působením lokální trivializace "narovnána" na pravoúhlou mřížku pokrývající obdélník ${\displaystyle \scriptstyle [-1/2,1/2]\times (0,5)}$. Vpravo je pak možno vidět analogickou situaci pro okolí ${\displaystyle \scriptstyle U_{2}}$ s trivializací ${\displaystyle \scriptstyle \varphi _{2}}$. Povšimněme si i směrů šipek ohraničujících dané úseky Möbiovy pásky.

Okolí ${\displaystyle \scriptstyle U_{1}}$ a ${\displaystyle \scriptstyle U_{2}}$ se překrývají v oblastech ${\displaystyle \scriptstyle (5-1/10,5)}$ a ${\displaystyle \scriptstyle (2\pi ,2\pi +1/10)}$. Označme si první interval písmenem ${\displaystyle \scriptstyle A=(5-1/10,5)}$ a druhý interval podobně písmenem ${\displaystyle \scriptstyle B=(2\pi ,2\pi +1/10)}$. Pro úplnost si odvodíme tvar přechodových funkcí ${\displaystyle \scriptstyle \tau _{12}}$ a ${\displaystyle \scriptstyle \tau _{21}}$. Vzhledem k tomu, že jedna je inverzí druhé, stačí spočíst ${\displaystyle \scriptstyle \tau _{12}:U_{1}\cap U_{2}\times F\to F}$. Zde je nutno pro každý z obou intervalů A a B hledat tvar přechodové funkce zvlášť. Pro všechny body ${\displaystyle \scriptstyle m=m(v)\in M}$, kde ${\displaystyle \scriptstyle v\in A}$, a pro všechny prvky vlákna ${\displaystyle \scriptstyle f=f(u)\in F}$, ${\displaystyle \scriptstyle u\in [-1/2,1/2]}$, platí

${\displaystyle (\varphi _{2}^{-1}\circ \varphi _{1})(m,f)=\varphi _{2}^{-1}((x(u,v),y(u,v),z(u,v)))=(m,f)}$.

Přechodová funkce ${\displaystyle \scriptstyle \tau _{12}^{A}:F\to F}$ je tedy identickým zobrazením. Explicitně,

${\displaystyle \tau _{12}^{m}(f(u))=f(u),\quad m=m(v),\ v\in A,\quad \forall u\in [-1/2,1/2]}$.

Podobně postupujeme i pro interval B, zde však musíme být více na pozoru. Proměnná ${\displaystyle \scriptstyle v}$, parametrizující kružnici, nabývá hodnot mezi nulou a ${\displaystyle \scriptstyle 2\pi }$. V intervalu B se však nacházejí čísla mimo tyto meze. Protože hodnotě ${\displaystyle \scriptstyle 2\pi +v\in [2\pi ,4\pi )}$ by měl odpovídat stejný bod kružnice jako hodnotě ${\displaystyle \scriptstyle v\in [0,2\pi )}$, vyjádřeme si proměnnou ${\displaystyle \scriptstyle v\in B}$ explicitně ve tvaru ${\displaystyle \scriptstyle 2\pi +v}$, kde už ${\displaystyle \scriptstyle v\in [0,1/10)\subset [0,2\pi )}$. Při tomto vyjádření přecházejí goniometrické funkce do tvarů

${\displaystyle \cos \left({\frac {v}{2}}\right)\rightarrow \cos \left({\frac {2\pi +v}{2}}\right)=\cos \left(\pi +{\frac {v}{2}}\right)=-\cos \left({\frac {v}{2}}\right)}$,

${\displaystyle \sin \left({\frac {v}{2}}\right)\rightarrow \sin \left({\frac {2\pi +v}{2}}\right)=\sin \left(\pi +{\frac {v}{2}}\right)=-\sin \left({\frac {v}{2}}\right)}$.

Vyjádření lokální trivializace ${\displaystyle \scriptstyle \varphi _{2}}$ tak přejde do tvaru

${\displaystyle {\begin{array}{rcl}x(u,v)&=&(1-u\cos({\frac {v}{2}}))\cos(v),\\y(u,v)&=&(1-u\cos({\frac {v}{2}}))\sin(v),\\z(u,v)&=&-u\,\sin({\frac {v}{2}}),\end{array}}}$

kde nyní parametr ${\displaystyle \scriptstyle v}$ nenabývá hodnot z intervalu B, ale z intervalu ${\displaystyle \scriptstyle [0,1/10)}$. Vidíme, že znaménko minus, objevivší se z úpravy goniometrických funkcí, můžeme přidružit k proměnné ${\displaystyle \scriptstyle u}$. Máme-li pevně zadán bod ${\displaystyle \scriptstyle (x,y,z)}$ Möbiovy pásky, jehož parametry v trivializaci ${\displaystyle \scriptstyle \varphi _{1}}$ mají hodnoty ${\displaystyle \scriptstyle u=u_{1}\in [-1/2,1/2]}$ a ${\displaystyle \scriptstyle v=v_{1}\in [0,1/10)}$, tak v trivializaci ${\displaystyle \scriptstyle \varphi _{2}}$ je tentýž bod popsán parametry o hodnotách ${\displaystyle \scriptstyle u=u_{2}\in [-1/2,1/2]}$ a ${\displaystyle \scriptstyle v=v_{2}\in [0,1/10)}$, kde však

${\displaystyle u_{2}=-u_{1},\quad v_{2}=v_{1}}$.

Z těchto vztahů okamžitě vidíme, že na intervalu B přechodová funkce ${\displaystyle \scriptstyle \tau _{12}^{B}:F\to F}$ efektivně obrací hodnotu parametru ${\displaystyle \scriptstyle u}$

${\displaystyle \tau _{12}^{m}(f(u))=f(-u),\quad m=m(v),\ v\in B,\quad \forall u\in [-1/2,1/2]}$.

Toto obracení parametru je explicitní vyjádření nespojitosti, se kterou jsme se setkali u zobrazení ${\displaystyle \scriptstyle \varphi :M\times F\to E}$ v předchozím pododdíle o lokálních trivializacích. Graficky pak obracení parametru ${\displaystyle \scriptstyle u}$ při přechodu od jedné trivializace ke druhé na intervalu ${\displaystyle \scriptstyle [0,1/10)}$ můžeme odtušit ze směru ohraničující šipky na Obr. 3, kde pro trivializaci ${\displaystyle \scriptstyle \varphi _{1}}$ směřuje daná šipka ven, zatímco u trivializace ${\displaystyle \scriptstyle \varphi _{2}}$ tato šipka směřuje dovnitř.

Jen tak na okraj, v případě válce (kde neuvažujeme jeho podstavy) k žádné podobné nespojitosti nedochází a celý válec tak lze popsat jediným okolím a jedinou lokální trivializací. Válec je tedy příkladem triviálního fibrovaného prostoru. Pokud bychom i přesto pokrývali válec dvěma okolími jako v případě Möbiovy pásky výše a zvolili bychom si přirozenou parametrizaci válcové plochy, tak přechodová funkce by byla na obou intervalech A i B identické zobrazení.

Na závěr tedy můžeme vyjádřit předpis přechodové funkce na celém průniku okolí ${\displaystyle \scriptstyle U_{1}}$ a ${\displaystyle \scriptstyle U_{2}}$ pro Möbiovu pásku způsobem

${\displaystyle \tau _{12}^{m(v)}(f(u))={\begin{cases}f(u)&v\in A,\\f(-u)&v\in B.\end{cases}}}$

Vektorový fibrovaný prostor (angl. vector bundle) je fibrovaný prostor, jehož typickým vláknem je vektorový prostor. Přechodové funkce v tomto případě tvoří strukturní grupu všech nesingulárních matic odpovídajících rozměrů. Je-li typické vlákno reálný vektorový prostor dimenze k, tj. ${\displaystyle \scriptstyle F=\mathbb {R} ^{k}}$, tak strukturní grupa je rovna maticové grupě ${\displaystyle \scriptstyle GL(\mathbb {R} ,k)}$. Podobně, pokud je typické vlákno rovno komplexnímu vektorovému prostoru ${\displaystyle \scriptstyle F=\mathbb {C} ^{k}}$, tak strukturní grupa je ${\displaystyle \scriptstyle GL(\mathbb {C} ,k)}$. Číslo k se nazývá dimenze vlákna a značí se, poněkud nekonzistentně, symbolem ${\displaystyle \scriptstyle \dim E}$.[1] (Ačkoli dimenze totálního prostoru E je rovna n + k, kde n je dimenze bázové variety M.) Důležitým příkladem vektorového fibrovaného prostoru je tečný fibrovaný prostor. Jiným příkladem je normálový fibrovaný prostor. Oba druhy jsou popsány v následujících pododdílech.

Jedním z důležitých příkladů fibrovaných prostorů je tzv. tečný fibrovaný prostor (někdy též tečný bandl, angl. tangent bundle), k němuž dojdeme následujícím postupem. Uvažujme nějakou (reálnou) diferencovatelnou varietu ${\displaystyle \scriptstyle M}$ konečné dimenze ${\displaystyle \scriptstyle \dim M=n}$. V každém bodě ${\displaystyle \scriptstyle m}$ této variety je definován tečný prostor ${\displaystyle \scriptstyle T_{m}M}$, což je vektorový prostor všech tečných vektorů k varietě ${\displaystyle \scriptstyle M}$ v bodě ${\displaystyle \scriptstyle m}$. Disjunktním sjednocením všech tečných prostorů

${\displaystyle TM=\coprod _{m\in M}T_{m}M}$

získáme totální prostor tečného fibrovaného prostoru. Disjunktním sjednocením je zde přitom míněno sjednocení, kde prvek z ${\displaystyle \scriptstyle TM}$ si „pamatuje“ nejen to, kam coby tečný vektor míří, ale i z jakého bodu variety vychází. Informaci o bodu variety, ze kterého daný prvek ${\displaystyle \scriptstyle p\in TM}$ vychází, nám přitom podá projekce ${\displaystyle \scriptstyle \pi :TM\to M}$. Matematicky zapsáno

${\displaystyle p\in T_{m}M\quad \Rightarrow \quad \pi (p)=m}$.

Bázovou varietou je tedy samotná varieta ${\displaystyle \scriptstyle M}$ a vláknem je vektorový prostor ${\displaystyle \scriptstyle \mathbb {R} ^{n}}$, neboť všechny tečné prostory ${\displaystyle \scriptstyle T_{m}M}$ pro libovolné ${\displaystyle \scriptstyle m\in M}$ jsou izomorfní ${\displaystyle \scriptstyle \mathbb {R} ^{n}}$.

Abychom mohli zavést lokální trivializace, uvažme nějaké otevřené pokrytí ${\displaystyle \scriptstyle \{U_{\alpha }\}_{\alpha }}$ variety ${\displaystyle \scriptstyle M}$ a z něho uvažujme právě jedno konkrétní okolí ${\displaystyle \scriptstyle U_{\alpha }}$ se souřadnicemi ${\displaystyle \scriptstyle \psi _{\alpha }:U_{\alpha }\to \mathbb {R} ^{n}}$. Souřadnice ${\displaystyle \scriptstyle \{x^{\mu }\}_{\mu =1}^{n}}$ bodu ${\displaystyle \scriptstyle m\in U_{\alpha }\subset M}$ variety tedy obdržíme ze vzorce ${\displaystyle \scriptstyle \{x^{\mu }\}_{\mu =1}^{n}=\psi _{\alpha }(m)}$. Každý bod variety ${\displaystyle \scriptstyle M}$ v okolí ${\displaystyle \scriptstyle U_{\alpha }}$ je tedy jednoznačně popsán ${\displaystyle \scriptstyle n}$-ticí čísel. Co víc, za bázi tečného prostoru ${\displaystyle \scriptstyle T_{m}M}$ si můžeme vzít derivace ${\displaystyle \scriptstyle \{\partial /\partial {x^{\mu }}\}_{\mu =1}^{n}}$. Každý vektor ${\displaystyle \scriptstyle X=X^{\mu }\partial /\partial x^{\mu }}$ z ${\displaystyle \scriptstyle T_{m}M}$ je tedy také určen ${\displaystyle \scriptstyle n}$-ticí čísel ${\displaystyle \scriptstyle \{X^{\mu }\}_{\mu =1}^{n}}$. Pro jednoznačnou identifikaci bodu ${\displaystyle \scriptstyle p}$ z množiny ${\displaystyle \scriptstyle \pi ^{(-1)}(U_{\alpha })}$ (tj. ze vzoru okolí ${\displaystyle \scriptstyle U_{\alpha }}$ při projekci ${\displaystyle \scriptstyle \pi }$) je tedy třeba znát ${\displaystyle \scriptstyle 2n}$ čísel

${\displaystyle (x^{1},\ldots ,x^{n},X^{1},\ldots ,X^{n})}$.

Za lokální trivializaci ${\displaystyle \scriptstyle \varphi _{\alpha }:U_{\alpha }\times \mathbb {R} ^{n}\to \pi ^{(-1)}(U_{\alpha })}$ tak můžeme vzít zobrazení, jehož inverze má v souřadnicích ${\displaystyle \scriptstyle \psi _{\alpha }}$ tvar

${\displaystyle \varphi _{\alpha }^{-1}(p)=(x^{1},\ldots ,x^{n},X^{1},\ldots ,X^{n})}$.

Tímto způsobem obdržíme lokální trivializace pro všechna pokrývací okolí. Tečný fibrovaný prostor je tedy fibrovaný prostor určený čtveřicí ${\displaystyle \scriptstyle (TM,M,\mathbb {R} ^{n},\pi )}$ a danými lokálními trivializacemi.

Řez tečného fibrovaného prostoru se nazývá vektorové pole. Každému bodu variety ${\displaystyle \scriptstyle M}$ je tedy přiřazen nějaký vektor a toto přiřazení je hladké.

Nechť ${\displaystyle \scriptstyle M}$ je ${\displaystyle \scriptstyle n}$-rozměrná diferencovatelná varieta vložená do prostoru ${\displaystyle \scriptstyle \mathbb {R} ^{n+k}}$. Dále nechť ${\displaystyle \scriptstyle N_{m}M}$ je ortogonální doplněk k ${\displaystyle \scriptstyle T_{m}M}$ ve vektorovém prostoru ${\displaystyle \scriptstyle \mathbb {R} ^{n+k}}$, kde ${\displaystyle \scriptstyle T_{m}M}$ značí tečný vektorový prostor k varietě ${\displaystyle \scriptstyle M}$ v bodě ${\displaystyle \scriptstyle m\in M}$. Platí tedy

${\displaystyle N_{m}M=\{v\in \mathbb {R} ^{n+k}|(\forall u\in T_{m}M)(v\cdot u=0)\}}$,

kde tečka značí standardní skalární součin. Z předchozího plyne, že vektorový prostor ${\displaystyle \scriptstyle N_{m}M}$ je izomorfní prostoru ${\displaystyle \scriptstyle \mathbb {R} ^{k}}$. Disjunktním sjednocením všech množin vznikne normálový fibrovaný prostor ${\displaystyle \scriptstyle NM}$ (angl. normal bundle), jehož typickým vláknem je ${\displaystyle \scriptstyle \mathbb {R} ^{k}}$. Explicitně tedy

${\displaystyle NM=\coprod _{p\in M}N_{p}M}$.

Mějme vektorový fibrovaný prostor ${\displaystyle \scriptstyle E{\stackrel {\pi }{\to }}M}$ s vláknem ${\displaystyle \scriptstyle F}$. K vektorovému prostoru ${\displaystyle \scriptstyle F}$ můžeme uvažovat prostor ${\displaystyle \scriptstyle F^{\ast }}$ k němu duální, jenž je tvořen všemi lineárními funkcionály. Tento prostor má stejnou dimenzi jako ${\displaystyle \scriptstyle F}$ a fibrovaný prostor, kde za vlákno vezmeme ${\displaystyle \scriptstyle F^{\ast }}$, nazýváme duální fibrovaný prostor (angl. dual bundle). Speciálním druhem duálního fibrovaného prostoru je kotečný fibrovaný prostor, jenž je definován níže.

Ke každému tečnému prostoru ${\displaystyle \scriptstyle T_{m}M}$ existuje prostor duální ${\displaystyle \scriptstyle T_{m}^{\ast }M}$, tvořený lineárními funkcionály definovanými nad vektory z ${\displaystyle \scriptstyle T_{m}M}$. Tomuto duálnímu prostoru se říká kotečný prostor k varietě ${\displaystyle \scriptstyle M}$ v bodě ${\displaystyle \scriptstyle m}$. Postupem analogickým tomu pro tečný fibrovaný prostor můžeme definovat tzv. kotečný fibrovaný prostor (někdy též kotečný bandl, angl. cotangent bundle). V případě kotečného fibrovaného prostoru je za bázovou varietu zvolena (reálná) diferencovatelná varieta ${\displaystyle \scriptstyle M}$ dimenze ${\displaystyle \scriptstyle \dim M=n}$, totální prostor se definuje jako disjunktní sjednocení duálních prostorů

${\displaystyle T^{\ast }M=\coprod _{m\in M}T_{m}^{\ast }M}$

a za vlákno se bere množina ${\displaystyle \scriptstyle \mathbb {R} ^{n}}$. Tato množina je totiž izomorfní duálnímu prostoru ${\displaystyle \scriptstyle T_{m}^{\ast }M}$ pro libovolný bod variety ${\displaystyle \scriptstyle m\in M}$. Projekce ${\displaystyle \scriptstyle \pi :T^{\ast }M\to M}$ je volena tak, aby pro každý prvek z ${\displaystyle \scriptstyle T^{\ast }M}$ vrátila bod variety, odkud tento prvek pochází. To jest

${\displaystyle \omega \in T_{m}^{\ast }M\quad \Rightarrow \quad \pi (\omega )=m}$.

Jak je zmíněno v předchozím pododdíle o tečném fibrovaném prostoru, pro každý tečný prostor ${\displaystyle \scriptstyle T_{m}M}$ k varietě ${\displaystyle \scriptstyle M}$ v bodě ${\displaystyle \scriptstyle m}$, kdy se bod ${\displaystyle \scriptstyle m}$ nachází v nějakém pokrývacím okolí ${\displaystyle \scriptstyle U_{\alpha }\subset M}$ popsaném souřadnicemi ${\displaystyle \scriptstyle \psi _{\alpha }(m)=\{x^{\mu }\}_{\mu =1}^{n}}$, můžeme za bázi tečného prostoru vzít množinu ${\displaystyle \scriptstyle \{\partial /\partial {x^{\mu }}\}_{\mu =1}^{n}}$ derivací podle daných souřadnic. V duálním prostoru ${\displaystyle \scriptstyle T_{m}^{\ast }M}$ dále můžeme uvažovat bázi souřadnicových funkcionálů ${\displaystyle \scriptstyle \{\mathrm {d} x^{\mu }\}_{\mu =1}^{n}}$, jejichž působení na vektorech alias derivacích lze vyjádřit elegantně ve tvaru