Parita funkce

V matematice některé funkce vykazují jisté druhy symetrie, označované jako parita. Konkrétně se funkce osově souměrné podle osy y označují jako sudé, zatímco funkce středově souměrné podle počátku jako liché funkce. Obecně funkce nemusí být ani lichá, ani sudá; a funkce konstantně rovná nule je zároveň sudá i lichá. Každou funkci, jejíž definiční obor je symetrický vůči počátku, lze jednoznačně vyjádřit jako součet jedné sudé a jedné liché funkce.

Sudé funkce

Sudá funkce: y = x²

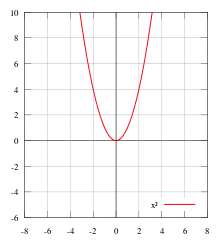
Funkce $f(x)$ je sudá funkce, pokud pro všechna $x$ , pro která je $f(x)$ definováno, je definováno i $f(-x)$ a platí $f(-x)=f(x)$ .

To právě znamená, že graf sudé funkce je osově souměrný podle osy y.

Mezi sudé funkce patří všechny mocninné funkce se sudým mocnitelem (např. x², x⁻⁴), dále také například konstantní funkce, absolutní hodnota nebo kosinus (i hyperbolický). Složitějším příkladem sudé funkce je Dirichletova funkce.

Liché funkce

Lichá funkce: y = x³

Funkce $f(x)$ je lichá funkce, pokud pro všechna $x$ , pro která je $f(x)$ definováno, je definováno i $f(-x)$ a platí $f(-x)=-f(x)$ .

To právě znamená, že graf liché funkce je středově souměrný podle počátku soustavy souřadnic.

Mezi liché funkce patří všechny mocninné funkce s lichým mocnitelem (např. x, x³, 1/x), dále také např. znaménková funkce sgn, sinus a tangens (i hyperbolické), stejně jako funkce k nim inverzní, tzn. cyklometrické funkce $\arcsin$ , $\arctan$ a hyperbolometrické $\arg \sinh$ , $\arg \tanh$ .

Vlastnosti

Základní vlastnosti

Pokud je lichá funkce definovaná v počátku, tak tam musí mít funkční hodnotu 0.
Funkce, která je zároveň sudá i lichá, je jedině nulová funkce f(x) = 0 (s definičním oborem symetrickým kolem nuly).
Sudá funkce nemůže být ryze monotónní (ledaže by byla triviálně definovaná jen v počátku).
Součet dvou sudých funkcí je sudá funkce, konstantní násobek sudé funkce je taktéž sudá funkce.
Součet dvou lichých funkcí je lichá funkce, konstantní násobek liché funkce je taktéž lichá funkce.
Součet liché a sudé funkce není ani lichá ani sudá funkce, ledaže by jeden ze sčítanců byla nulová funkce (viz níže rozklad na sudou a lichou část).
Součin dvou sudých funkcí je sudá funkce, součin dvou lichých funkcí je také sudá funkce.
Součin liché funkce a sudé funkce je lichá funkce.
Inverzní funkce k liché funkci je lichá funkce.
Složená funkce s vnitřní funkcí sudou a libovolnou vnější funkcí je sudá. Složená funkce s vnitřní funkcí lichou je lichá pro vnější funkci lichou a sudá pro vnější funkci sudou.

Algebraické vlastnosti

Lineární kombinace sudých funkcí je sudá funkce, sudé funkce tvoří vektorový prostor nad reálnými čísly. Obdobně je lineární kombinace lichých funkcí lichá funkce a liché funkce tvoří vektorový prostor nad reálnými čísly.
Vektorový prostor všech reálných funkcí je direktní součet vektorových prostorů sudých a lichých funkcí, tzn. libovolnou funkci (s definičním oborem symetrickým kolem nuly) lze jednoznačně rozložit na součet sudé a liché funkce:

f(x)={\frac {f(x)+f(-x)}{2}}+{\frac {f(x)-f(-x)}{2}}

Např. přirozená exponenciála se takto rozkládá na svou sudou část – hyperbolický kosinus a lichou část – hyperbolický sinus:

e^{x}=\cosh x+\sinh x

Množina sudých funkcí tvoří nad reálnými čísly algebru, množina lichých funkcí nikoliv.

Analytické vlastnosti

Derivace sudé funkce je lichá funkce, derivace liché funkce je sudá funkce.
Libovolná primitivní funkce k liché funkci definované na intervalu je sudá funkce, ale nejvýše jedna primitivní funkce k sudé funkci může být lichá.
Taylorův polynom sudé funkce v počátku obsahuje pouze sudé mocniny, u liché funkce obsahuje pouze liché mocniny.
Taylorova řada sudé funkce v počátku (tj. Maclaurinova řada) obsahuje pouze sudé mocniny, u liché funkce obsahuje pouze liché mocniny.
Fourierova řada periodické sudé funkce obsahuje pouze kosinové členy, Fourierova řada periodické liché funkce obsahuje pouze sinové členy.

Související články

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.