Mocninná funkce

Mocninná funkce je elementární matematická funkce, jejíž hodnoty jsou přímo úměrné určité mocnině proměnné, tedy funkce tvaru

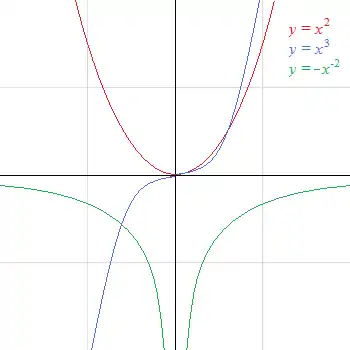
f\colon x\mapsto ax^{r}\qquad a,r\in \mathbb {R} ,

Grafy mocninných funkcí x², x³ a −x⁻²

kde $a$ a $r$ jsou konstanty a $x$ je proměnná. Konstanta $r$ se nazývá exponent.

Mocninná funkce, jejíž exponent $r$ je celé číslo nebo nula, je polynomiální funkce s nejvýše jedním nenulovým koeficientem.

Definiční obor

Definiční obor závisí na exponentu $r$ , konkrétně na jeho celočíselnosti (tj. zda $r\in \mathbb {Z}$ ) a znaménku podle následující tabulky.

	$r>0$	$r<0$	$r=0$
$r\in \mathbb {Z}$	$\mathbb {R}$	$\mathbb {R} \setminus \{0\}$	$\mathbb {R} \setminus \{0\}$ nebo $\mathbb {R}$ [pozn. 1]
$r\notin \mathbb {Z}$	$\mathbb {R} _{0}^{+}$	$\mathbb {R} ^{+}$	—

Obecně není výraz 0⁰ definován. V případě mocninné funkce je však smysluplné jej dodefinovat vztahem 0⁰ = 1, díky čemuž při $r=0$ se mocninná funkce zredukuje na konstantu $f(x)=a$ s definičním oborem $\mathbb {R}$ .

Obor hodnot závisí na konstantě $a$ a exponentu $r$ .

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.