Hyperbolické funkce

sinh, cosh a tanh

csch, sech a coth

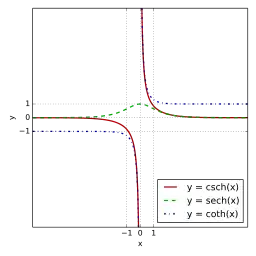
Hyperbolické funkce jsou definovány následovně:

• Hyperbolický sinus:

${\displaystyle \sinh x={\frac {e^{x}-e^{-x}}{2}}={\frac {e^{2x}-1}{2e^{x}}}}$

• Hyperbolický kosinus:

${\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}}={\frac {e^{2x}+1}{2e^{x}}}}$

• Hyperbolický tangens:

${\displaystyle \tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}={\frac {e^{2x}-1}{e^{2x}+1}}}$

• Hyperbolický kotangens:

${\displaystyle \coth x={\frac {\cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}={\frac {e^{2x}+1}{e^{2x}-1}}}$

• Hyperbolický sekans:

${\displaystyle \operatorname {sech} \,x=\left(\cosh x\right)^{-1}={\frac {2}{e^{x}+e^{-x}}}={\frac {2e^{x}}{e^{2x}+1}}}$

• Hyperbolický kosekans:

${\displaystyle \operatorname {csch} \,x=\left(\sinh x\right)^{-1}={\frac {2}{e^{x}-e^{-x}}}={\frac {2e^{x}}{e^{2x}-1}}}$

kde e je Eulerovo číslo.

Hyperbolické funkce mohou být také definovány pomocí imaginárního úhlu:

• Hyperbolický sinus:

${\displaystyle \sinh x=-{\rm {i}}\sin {\rm {i}}x\!}$

• Hyperbolický kosinus:

${\displaystyle \cosh x=\cos {\rm {i}}x\!}$

• Hyperbolický tangens:

${\displaystyle \tanh x=-{\rm {i}}\tan {\rm {i}}x\!}$

• Hyperbolický kotangens:

${\displaystyle \coth x={\rm {i}}\cot {\rm {i}}x\!}$

• Hyperbolický sekans:

${\displaystyle \operatorname {sech} \,x=\sec {{\rm {i}}x}\!}$

• Hyperbolický kosekans:

${\displaystyle \operatorname {csch} \,x={\rm {i}}\,\csc \,{\rm {i}}x\!}$

kde i je imaginární číslo definované jako i² = −1.

Tyto komplexní tvary jsou odvozeny z Eulerova vzorce.

Sudost

${\displaystyle \cosh(-x)=\cosh x\,\!}$

${\displaystyle \operatorname {sech} (-x)=\operatorname {sech} \,x\,\!}$

Lichost

${\displaystyle \sinh(-x)=-\sinh x\,\!}$

${\displaystyle \tanh(-x)=-\tanh x\,\!}$

${\displaystyle \coth(-x)=-\coth x\,\!}$

${\displaystyle \operatorname {csch} (-x)=-\operatorname {csch} \,x\,\!}$

Hyperbolický sinus a kosinus splňují podmínku:

${\displaystyle \cosh ^{2}x-\sinh ^{2}x=1\,}$

a podobně:

${\displaystyle \tanh ^{2}x=1-\operatorname {sech} ^{2}x}$

${\displaystyle \coth ^{2}x=1+\operatorname {csch} ^{2}x}$

${\displaystyle {\frac {d}{dx}}\sinh x=\cosh x\,}$

${\displaystyle {\frac {d}{dx}}\cosh x=\sinh x\,}$

${\displaystyle {\frac {d}{dx}}\tanh x=1-\tanh ^{2}x={\hbox{sech}}^{2}x=1/\cosh ^{2}x\,}$

${\displaystyle {\frac {d}{dx}}\coth x=1-\coth ^{2}x=-{\hbox{csch}}^{2}x=-1/\sinh ^{2}x\,}$

${\displaystyle {\frac {d}{dx}}\ {\hbox{csch}}\,x=-\coth x\ {\hbox{csch}}\,x\,}$

${\displaystyle {\frac {d}{dx}}\ {\hbox{sech}}\,x=-\tanh x\ {\hbox{sech}}\,x\,}$

${\displaystyle {\frac {d}{dx}}\,\operatorname {arsinh} \,x={\frac {1}{\sqrt {x^{2}+1}}}}$

${\displaystyle {\frac {d}{dx}}\,\operatorname {arcosh} \,x={\frac {1}{\sqrt {x^{2}-1}}}}$

${\displaystyle {\frac {d}{dx}}\,\operatorname {artanh} \,x={\frac {1}{1-x^{2}}}}$

${\displaystyle {\frac {d}{dx}}\,\operatorname {arcsch} \,x=-{\frac {1}{\left|x\right|{\sqrt {1+x^{2}}}}}}$

${\displaystyle {\frac {d}{dx}}\,\operatorname {arsech} \,x=-{\frac {1}{x{\sqrt {1-x^{2}}}}}}$

${\displaystyle {\frac {d}{dx}}\,\operatorname {arcoth} \,x={\frac {1}{1-x^{2}}}}$

Pro kompletní seznam integrálů přejděte na Seznam integrálů hyperbolických funkcí.

${\displaystyle \int \sinh ax\,dx=a^{-1}\cosh ax+C}$

${\displaystyle \int \cosh ax\,dx=a^{-1}\sinh ax+C}$

${\displaystyle \int \tanh ax\,dx=a^{-1}\ln(\cosh ax)+C}$

${\displaystyle \int \coth ax\,dx=a^{-1}\ln(\sinh ax)+C}$

${\displaystyle \int {\frac {du}{\sqrt {a^{2}+u^{2}}}}=\sinh ^{-1}\left({\frac {u}{a}}\right)+C}$

${\displaystyle \int {\frac {du}{\sqrt {u^{2}-a^{2}}}}=\cosh ^{-1}\left({\frac {u}{a}}\right)+C}$

${\displaystyle \int {\frac {du}{a^{2}-u^{2}}}=a^{-1}\tanh ^{-1}\left({\frac {u}{a}}\right)+C;u^{2}<a^{2}}$

${\displaystyle \int {\frac {du}{a^{2}-u^{2}}}=a^{-1}\coth ^{-1}\left({\frac {u}{a}}\right)+C;u^{2}>a^{2}}$

${\displaystyle \int {\frac {du}{u{\sqrt {a^{2}-u^{2}}}}}=-a^{-1}\operatorname {sech} ^{-1}\left({\frac {u}{a}}\right)+C}$

${\displaystyle \int {\frac {du}{u{\sqrt {a^{2}+u^{2}}}}}=-a^{-1}\operatorname {csch} ^{-1}\left|{\frac {u}{a}}\right|+C}$

kde C je integrační konstanta.

• Hyperbola

V tomto článku byl použit překlad textu z článku Hyperbolic function na anglické Wikipedii.

• Obrázky, zvuky či videa k tématu hyperbolická funkce na Wikimedia Commons
• (anglicky)Hyperbolické funkce Archivováno 18. 2. 2012 na Wayback Machine na PlanetMath
• (anglicky)Hyperbolické funkce na MathWorld