Periodická funkce
Periodická funkce je v matematice funkce, jejíž hodnoty se pravidelně opakují s určitou periodou. Nejdůležitější periodické funkce jsou trigonometrické funkce (sinus, kosinus atd.), jejichž periodou je 2π. Graf periodické funkce se také opakuje a lze jej sestrojit kopírováním jedné periody na ose x.
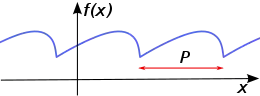
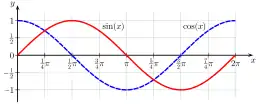

Periodické funkce se užívají ve fyzice i v technice k popisu vlnových dějů, oscilací, cyklů a mnoha dalších pravidelných dějů. Nezávislou proměnnou bývá čas. Rozdíl mezi minimem a maximem periodické funkce se nazývá amplituda a převrácená hodnota periody je frekvence.
Funkce, které nejsou periodické, se nazývají aperiodické.
Definice
Přesněji můžeme říci, že funkce je periodická s periodou , jestliže
pro všechny hodnoty v definiční oblasti . Pro všechna celá čísla n také platí
Jednoduchým příkladem je funkce, jejíž hodnota je desetinná část argumentu, takže například
Perioda funkce je rovna 1 a .
Nejmenší kladné číslo , které je periodou periodické funkce, označujeme jako primitivní perioda. Průběh periodické funkce je v každém intervalu stejný.
Obecná definice
Nechť je množina s interní operací . Potom P-periodickou funkcí nebo periodickou funkcí s periodou P na je funkce na taková, že
- .
Poznamenejme, že ačkoliv se předpokládá, že je komutativní, v této definici píšeme napravo.
Funkce, jejichž definičním oborem jsou komplexní čísla, mohou mít dvě nesouměřitelné periody, aniž by se jednalo o konstantní funkce. Takovými funkcemi jsou např. eliptické funkce. („Nesouměřitelnost“ zde znamená, že jedna z period není celočíselným násobkem druhé.)
Periodické řady
Některé přirozeně se vyskytující řady jsou periodické, například desetinný rozklad libovolného racionálního čísla (viz periodický rozvoj). Můžeme proto mluvit o periodě nebo délce periody řady. Jedná se tedy o speciální případ obecné definice.
Základem Fourierových řad je myšlenka, že libovolná periodická funkce je součtem trigonometrických funkcí s periodami P, 2P, 3P atd.
Translační symetrie
Jestliže se k popisu nějakého objektu použije funkce, např. nekonečný obraz může být popsán barvou jako funkcí pozice, odpovídá periodicita této funkce translační symetrii objektu.
Související články
- Téměř periodické funkce
- Amplituda
- Frekvence
- Oscilace
- Vlnová délka