Johann Heinrich Lambert
Johann Heinrich Lambert (26. srpen 1728, Mylhúzy – 25. září 1777, Berlín) byl švýcarský matematik, fyzik, astronom a filozof narozený v Alsasku, na území dnešní Francie. Většinu svých děl psal německy. Proslul především svým matematickým důkazem, že číslo π je iracionální. Jako první též aplikoval hyperbolické funkce v trigonometrii. Jeho studie o kuželosečce umožnily přesnější a jednodušší výpočty drah komet. Spekuloval i o neeuklidovském prostoru. Známý je též jeho vzorec určující vztah mezi úhly a plochou hyperbolického trojúhelníku. Patřil k průkopníkům kartografické projekce. Vynalezl první vlhkoměr. V oblasti optiky významně přispěl k formulování Beer–Lambertova zákona a definoval Lambertův kosinus zákon. Jeho astronomické práce patřily k prvním, které rozvíjely mlhovinovou hypotézu. Významná je jeho teorie světla (fotometrie), proto po něm byla pojmenována jednotka světelného jasu. Ve filozofii je nejznámější jeho kniha Neues Organon, kde zkoumal vztah subjektivního a objektivního a věnoval se sylogistice. Známá je jeho korespondence s Immanuelem Kantem.
| Johann Heinrich Lambert | |
|---|---|
 | |
| Narození | 26. srpna 1728 Mylhúzy |
| Úmrtí | 25. září 1777 (ve věku 49 let) Berlín |
| Příčina úmrtí | Tuberkulóza |
| Bydliště | Švýcarsko, Prusko |
| Země | Německo |
| Povolání | matematik, astronom, fyzik, filozof a spisovatel |
| Nábož. vyznání | protestantismus |
| Rodiče | Lukas Lambert, Elisabeth Schmerber |
| Některá data mohou pocházet z datové položky. | |
Život
Johann Heinrich Lambert se narodil roku 1728 ve městě Mylhúzy. Pocházel ze skromné rodiny. Kvůli špatné finanční situaci rodiny, mu nezbývalo nic jiného než se vzdát svého snu o vzdělání. Ve 12 letech musel opustit školu a začal pomáhat svému otci, který byl krejčím. Ve svém volném čase se věnoval samostudiu, hlavně pak studiu francouzského a latinského jazyka. V 15 letech, vzhledem k jeho vynikajícímu rukopisu, pracoval jako úředník v železárnách v Seppois. O dva roky později byl jmenován jako sekretář Johanna Rudolfa Iselina, redaktora Balera Zeitunga a později profesora práva na univerzitě v Basileji. Poté začal Lambert studovat v oboru filozofie a humanitních a přírodních věd. Nicméně svůj zájem věnoval spíše matematice a astronomii.[2]
Ve věku 20 let se stal soukromým učitelem synů hraběte Salis z Chur, kterým byl bezmála 10 let. Během těchto let se také spřátelil se členy šlechtických rodin ze Švýcarska. Mezi předměty, které své žáky učil, patřila: matematika, zeměpis, dějepis, katechismus a v neposlední řadě také jazyky. Během této doby, svou touhu po poznání uspokojoval studiem v rodinné knihovně. Zde byly položeny základy pro Lambertovu vědeckou kariéru. Deník Monatsbuch, který začal psát roku 1752, zaznamenává jeho práci měsíc po měsíci. V psaní deníku pokračoval až do své smrti. Během těchto let se zapojil do astronomických pozorování a zkonstruoval několik přístrojů pro vědecké experimenty. Lambert získal členství v literárních a vědeckých spolcích v Basileji. Na žádost Švýcarské vědecké obce, začal s pravidelným meteorologickým pozorováním, jehož výsledky prezentoval roku 1755.[3]
Od rodu 1756 do roku 1758, spolu se svými studenty, podnikl několik expedičních cest do Evropy, což mu dalo jedinečnou možnost setkat se s matematiky v německých a italských státech, Nizozemsku a Francii. Jejich první zastávkou byl Göttingen, kde se Lambert zúčastnil přednášky Bernoulise a Eulera. Zde se také seznámil s astronomem Tobiasem Mayerem. Další dva roky strávil v Nizozemsku a to především v Utrechtu, kde se seznámil s vyhlášenými fyziky. Jednou z nejdůležitějších událostí Lambertova života bylo vydání jeho knihy „Les propriétés remarquables de la route de la lumière par les airs et en général par plusieurs milieux réfringens, sphériques et concentriques“. Roku 1758 se vrátil, společně se svými studenty, zpět do Chur, kde se se svými studenty a s jejich rodinou rozešel.[3]
Doufal, že si najde stálou pozici na univerzitě v Göttingenu. Avšak to se zdálo jako nedosažitelné, a tak se přesunul do Curychu. Zde se zapojil do astronomického pozorování a byl zvolen členem městské vědecké obce. Během pobytu v Curychu publikoval knihu „Die freie Perspektive oder Anweisung jeden perspektivischen Aufriß von freyen Stücken und ohne Grundriß zu verfertigen“. Poté se vrátil zpět do rodných Mylhúz, kde strávil několik měsíců se svou rodinou.[2]
Následující roky pro něho byly poněkud hektické. V roce 1759 se spřátelil se slavným výrobcem vědeckých přístrojů Georgem Friedrichem Branderem. Přijal nabídku z Bavorské akademie věd, avšak rozdílné názory zapříčinili, že zde dlouho nevydržel. Chvíli poté dostal nabídku z Pruské vědecké akademie v Berlíně, kterou přijal. Byl přivítán skupinou švýcarských vědců v čele s Johannem Georgem Sulzerem. Kvůli svému chování a odlišným názorům byl jmenován až v roce 1765. Král Fridrich II. Veliký dokonce řekl, že byl na akademii přijat zatím „největší hlupák“. Nicméně Fridrich II. Veliký brzo změnil svůj názor. Uchvácen jeho věděním a myšlením mu nejen zvýšil plat, ale také ho jmenoval členem nové hospodářské komise akademie. Navíc byl zvolen do výboru pro zlepšení zeměměřičství. Pro jeho přínos akademii byl v roce 1770 poctěn titulem.[2][3]
Práce
Matematika
Lambert jako první člověk zavedl pojem hyperbolické funkce v trigonometrii. Cílem bylo snížit množství výpočtů při řešení goniometrických problémů. Navíc vyřešil goniometrické rovnice pomoci nekonečné řady.[3] Také se zajímal o neeuklidovský prostor. Dalším jeho významným příspěvkem v oblasti matematiky byl jeho důkaz, že Eulerovo číslo a číslo pí jsou iracionální[4], ke kterému použil řetězový zlomek pro funkci tan x.[5]
Mapové zobrazení
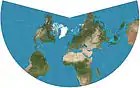

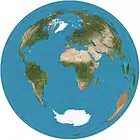
Lambert byl první matematik, který se dokázal vypořádat s obecnými vlastnostmi kartografických zobrazení a významně přispěl k teorii konstrukce map. Poprvé uvedl matematické podmínky pro mapové zobrazení (zachování úhlů a ploch) a provedl i jejich praktické návrhy. Také popsal konstrukci křivky určující skutečnou vzdálenost mezi dvěma místy na mapě. To vše pro sedm jím zveřejněných mapových zobrazení. Jeho mapové zobrazení jsou stále základem pro moderní teorie v této oblasti.[2] Ačkoliv Lambert svým zobrazením nedal jméno, dnes jsou známa jako Lambertovo konformní kuželové, Transverzální Mercatorovo, Lambertovo ekvivalentní azimutální, Lagrange-Lambertovo, Lambertovo ekvivalentní válcové, transverzální ekvivalentní válcové a Lambertovo ekvivalentní kónické zobrazení. První tři mají zásadní význam.
- Lambertovo konformní kuželové zobrazení – Hodně se používá u leteckých map a využívá ho mnoho národních a regionálních mapovacích systému po celém světě. Je to také nejpoužívanější kuželové zobrazení pro mapy, jednotlivých států a oblastí. Zemský povrch je zde převeden na konformní (stejnoúhlý) kužel s jednou nezkreslenou rovnoběžkou. Kužel je rozbalený a rovnoběžce, která se dotýká povrchu sféroidu, je přiřazena jednotková stupnice. Této rovnoběžce se říká standardní nebo základní rovnoběžka. Rovnoběžky se zobrazují jako koncentrické kružnice, jejichž střed leží na vrcholu kužele. Poledníky se zde zobrazují jako přímky střetávající se ve společném bodě (ve vrcholu kužele) často za hranicemi mapy.[6]
- Transverzální Mercatorovo zobrazení - Toto zobrazení se hojně používá v národním a mezinárodním mapování po celém světě. Jedná se o válcové zobrazení, kdy se válec dotýká referenční koule podél zvoleného poledníku. Zkreslení kolem zvoleného poledníku je do vzdálenosti 110 km velice přesné. S nárůstem vzdálenosti od zvoleného poledníku narůstá hodnota zkreslení. Základní poledník a poledníky od něho v 90° východním i západním směrem jsou zde zobrazeny jako přímky. Ostatní poledníky jsou vyobrazeny jako složité křivky. Rovnoběžky zde tvoří složité, uzavřené křivky. Díky své konformitě se toto zobrazení hojně používá pro geodetické účely.[7]
- Lambertovo ekvivalentní azimutální zobrazení – Zobrazení je vhodné pro zobrazení polárních oblastí a pro mapy hemisfér (východní a západní). Dalším příkladem využití jsou školní nástěnné mapy a atlasy. Používá ho také Evropská agentura pro životní prostředí. Charakteristickým znakem je zmenšování obrazu poledníkového úseku mezi 2 rovnoběžkami (se stejnými šířkovými odlehlostmi) směrem od středu mapy.[8]
Fyzika
Lambert vynalezl první praktický vlhkoměr. V roce 1760 vydal knihu „Photometria sive de mensure et gradibus luminis colorum et umbra", která se zabývala fotometrii a konceptem světla. V této knize zmínil základní předpoklady pro osvětlení. Jako první formuloval zákon o absorpci světla, známý také jako Beer-Lambertův zákon.[3] Je to matematické vyjádření závislosti absorpce elektromagnetického záření od vlastností materiálu, přes který záření prochází. Beer-Lambertův zákon zní přesně takto „Prochází-li světelný paprsek prostředím, které je schopno absorbovat, je intenzita paprsku vstupujícího vyšší než intenzita paprsku prošlého tímto prostředím“.[9] Také jako první přišel s termínem „albedo“.[3][10]
Filozofie
Lambert také zaujímá místo v historii filozofie. Zajímal se především o logiku. V návaznosti na nápady Leibnize, se pokusil vytvořit „ars characteristica combinatoria“ neboli logický kalkul. Jeho nejvýznamnější vydanou knihou v oblasti filozofie byla kniha „Neues Organon oder Gedanken über die Erforschung und Bezeichnung des Wahren und dessen Unterscheidung vom Irrthum und Schein“ vydaná v roce 1764. V této knize shrnuje úvahy o logické stavbě poznání, pravidlech myšlení a metodách vědeckých důkazů, rozvíjí myšlenky symbolického jazyka s cílem omezit nejednoznačnost pojmů.[11][12] Ve své druhé velké filozofické práci „Anlage zur Architektonik oder Theorie des Einfachen und Ersten in der philosophischen und mathematischen Erkenntniß“ navrhl reformu v metafyzice, pramenící z nespokojenosti s Wolfovým systémem. Od roku 1765 si dopisoval s Immanuelem Kantem, který poté zamýšlel, že by mu věnoval knihu „Kritika čistého rozumu“. Nicméně práce na knize byla zpožděna a kniha byla vydána až po Lambertově smrti.[13]
Astronomie
Lambertův příspěvek v astronomii je pozoruhodný. Je známo, že se zajímal o geometrii kuželoseček. Přišel s jednoduchými výpočty drah komet. Lambert ve své knize „Cosmologische Briefe über die Einrichtung des Weltbaues“ rozvinul teorii vesmíru a mlhovinovou hypotézu. V knize došel k závěru, že hvězdy kolem Slunce jsou součástí skupiny, která spolu putuje po Mléčné dráze. Dále přišel s teorií, že je v galaxii mnoho takových seskupení (hvězdných systémů).[3] V roce 1770 navrhl jednoduchou metodu určení, zda je vzdálenost mezi Zemí a Sluncem větší než vzdálenost od Země k dané kometě. Založil astronomický časopis „Berliner astronomisches Jahrbuch order Ephermeriden“ a navrhl zveřejnění specializovaných trigonometrických a astronomických tabulek, za účelem zjednodušení rutinní práce.[10][14]
Bibliografie
- Les propriétés remarquables de la route de la lumière par les airs et en général par plusieurs milieux réfringens, sphériques et concentriques (1758)
- Die freie Perspektive oder Anweisung jeden perspektivischen Aufriß von freyen Stücken und ohne Grundriß zu verfertigen (1759)
- Photometria sive de mensure et gradibus luminis colorum et umbra (1760)
- Insigniores orbitae cometarum proprietates (1761)
- Cosmologische Briefe über die Einrichtung des Weltbaues (1761)
- Neues Organon oder Gedanken über die Erforschung und Bezeichnung des Wahren und dessen Unterscheidung vom Irrthum und Schein (1764)
- Beyträge zum Gebrauche der Mathematik und deren Anwendung (1765)
- Anmerkungen über die Gewalt des Schiesspulvers und den Widerstand der Luft (1766)
- Zusätze zu den logarithmischen und trigonometrischen Tabellen, zur Erleichterung und Abkürzung der bey Anwendung der Mathematik vorfallenden Berechnungen (1770)
- Anlage zur Architektonik oder Theorie des Einfachen und Ersten in der philosophischen und mathematischen Erkenntniß (1771)
- Beschreibung einer mit Calauischem Wachse ausgemalten Farben-Pyramide, wo die Mischung jeder Farbe aus weiß und drey Grundfarben angeordnet, dargelegt und derselben Berechnung und vielfacher Gebrauch gewiesen wird. (1772)
- Pyrometrie oder vom Maaße des Feuers und der Wärme (1779)
Odkazy
Reference
- Antonín Rükl: Atlas Měsíce, Aventinum (Praha 1991), kapitola Pytheas, str. 66, č. mapového listu 20, ISBN 80-85277-10-7
- www.encyclopedia.com [online]. www.encyclopedia.com [cit. 2016-03-15]. Dostupné online.
- www.thefamouspeople.com [online]. www.thefamouspeople.com [cit. 2016-03-15]. Dostupné online.
- www-history.mcs.st-and.ac.uk [online]. www-history.mcs.st-and.ac.uk [cit. 2016-03-15]. Dostupné online.
- Lambert, Johann Heinrich (1762). "Mémoire sur quelques propriétés remarquables des quantités transcendentes circulaires et logarithmiques". Histoire de l'Académie (Berlin, published 1768) XVII: 265–322
- old.gis.zcu.cz [online]. old.gis.zcu.cz [cit. 2016-03-15]. Dostupné v archivu pořízeném dne 2016-04-14.
- old.gis.zcu.cz [online]. old.gis.zcu.cz [cit. 2016-03-15]. Dostupné v archivu pořízeném dne 2016-04-13.
- geomatika.kma.zcu.cz [online]. geomatika.kma.zcu.cz [cit. 2016-03-15]. Dostupné online.
- [online]. [cit. 2016-03-16]. Dostupné z: http://ciselniky.dasta.mzcr.cz/CD/hypertext/AJBDN.htm
- GRAY, J. J. Johann Heinrich Lambert, mathematician and scientist, 1728 – 1777. Historia Mathematica. 1978-02-01, roč. 5, čís. 1, s. 13–41. Dostupné online [cit. 2016-03-17]. DOI 10.1016/0315-0860(78)90133-7.
- Archivovaná kopie. www.eprojekt.gjs.cz [online]. [cit. 2016-03-17]. Dostupné v archivu pořízeném dne 2016-03-25.
- MARTIN, Thierry. J.-H. Lambert’s theory of probable syllogisms. International Journal of Approximate Reasoning. 2011-02-01, roč. 52, čís. 2, s. 144–152. Dostupné online [cit. 2016-03-17]. DOI 10.1016/j.ijar.2009.06.011.
- O'Leary M., Revolutions of Geometry, London:Wiley, 2010, p.385
- VOLKERT, Klaus Thomas. La théorie des lignes parallèles de Johann Heinrich Lambert, A. Papadoupoulos, G. Théret. Blanchard, Paris (2004). Historia Mathematica. Dostupné online [cit. 2016-03-17]. DOI 10.1016/j.hm.2015.04.003.