Mapové zobrazení

Mapové zobrazení, často též kartografická projekce, je způsob, jakým se převádí zobrazení povrchu Země (či jiného nebeského tělesa) z trojrozměrného zakřiveného povrchu referenčního elipsoidu či koule do roviny. Výsledek takového geometrického či početního postupu nazýváme mapa. Nejčastěji bývá na mapě sever směrem nahoru, jih směrem dolů, východ směrem doprava a západ směrem doleva.

Kartografické zkreslení

Protože povrch koule či elipsoidu není rozvinutelný do roviny (stejně jako nelze do roviny bez deformace rozvinout oloupanou slupku pomeranče), je zapotřebí převést jej na povrch některého geometrického objektu, jehož povrch do roviny rozvinutelný je. Takovými objekty jsou válec, kužel a také rovinná plocha sama. Převod kulové plochy do roviny znamená vždy tvarové zkreslení části obsažených informací. Ve výsledném rovinném zobrazení nemohou být současně zachovány všechny hlavní údaje – délky, úhly a plochy – vždy dochází ke zkreslení některého z nich (případně všech). Proto byla postupem času vyvinuta řada mapových zobrazení, z nichž každé klade důraz na jiný z důležitých údajů. Při vytváření map malých území (do několika set km²[zdroj?!]) je zkreslení téměř zanedbatelné, je-li však třeba zachytit na mapě větší oblast (kraj, stát, světadíl, oceán či celou Zemi), je nutné pečlivě volit mapové zobrazení tak, aby odpovídalo účelu mapy.

Nejpoužívanější mapy na amerických školách používají Mercatorovo mapové zobrazení,[zdroj?!] to je však kritizované za („kolonialistické“) zvětšení oblastí dále od rovníku.[1] Gall-Petersovo zobrazení ukazuje správné velikosti území, tvary a úhly ale neodpovídají skutečnosti. Instituce National Geographic Society dříve používala Robinsonovo zobrazení, v roce 1998 však bylo nahrazeno Winkelovým zobrazením, které minimalizuje všechny tři typy zkreslení: plochy, úhly i délky.[2]

Populární mapová zobrazení
  • Mercatorovo zobrazení (1569)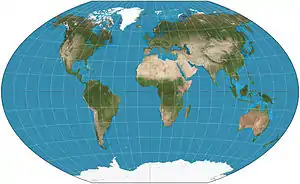
  • Winkelovo zobrazení (1921)
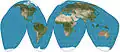  • Goodeho zobrazení (1923)
  • Zobrazení Dymaxion (1954)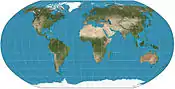
  • Robinsonovo zobrazení (1963)
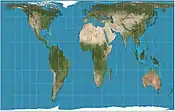  • Gall-Petersovo zobrazení (1973)

Třídění mapových zobrazení
Různá mapová zobrazení

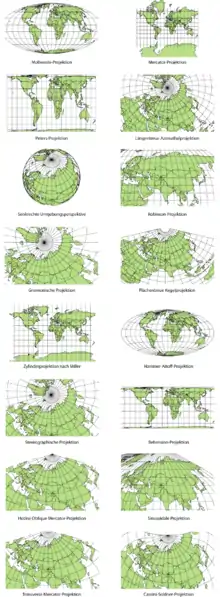
Mapová zobrazení podle kartografického zkreslení
  • ekvidistantní (délkojevná, stejnodélková) – nezkreslují vzdálenosti v určitém směru (netýká se všech délek)
  • ekvivalentní (plochojevná, stejnoplochá) – zachovávají poměry ploch, jsou však zkresleny úhly
  • konformní (úhlojevná, stejnoúhlá) – věrně zachycují úhly, ale silně zkreslují plochy
  • vyrovnávací (kompenzační) – kompromisní zobrazení s mírným zkreslením úhlů i ploch; do této kategorie lze počítat i mnohá zobrazení délkojevná

Mapová zobrazení podle vzhledu zobrazovací plochy
  • jednoduchá
  • nepravá (pseudo-zobrazení) – odvozená z výše uvedených zobrazení azimutálních, kuželových a válcových (např. Mollweidovo zobrazení)
  • mnohokuželová (polykónická) – místo jednoho kuželového pláště je použita soustava kuželů
  • zobrazení po vymezených částech – nejedná se vlastně o druh zobrazení, ale o opakování téhož způsobu zobrazení po malých územích, čímž je minimalizováno zkreslení

Mapová zobrazení podle polohy osy zobrazovací plochy
  • normální (pólová) – osa válce nebo kužele je totožná s osou glóbu nebo se zobrazovací rovina dotýká glóbu na jednom pólu
  • příčná (transverzální, rovníková) – osa válce nebo kužele leží v rovině rovníku nebo se zobrazovací rovina dotýká glóbu na rovníku
  • obecná (šikmá) – osa válce nebo kužele prochází středem glóbu, ale nesplývá s jeho osou ani neleží na rovníku nebo se zobrazovací rovina dotýká glóbu v libovolném bodě mezi pólem a rovníkem

Reference
  1. https://www.businessinsider.com.au/boston-school-gall-peters-map-also-wrong-mercator-2017-3 - Some US schools have introduced a new world map — but it’s just as wrong as the one you’re familiar with
  2. SINGH, Ishveena. Which is the best map projection?. Geoawesomeness [online]. 2017-04-25 [cit. 2021-02-25]. Dostupné online. (anglicky)

Externí odkazy
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.