Kružnice opsaná

• Velikost poloměru opsané kružnice určuje vztah

${\displaystyle r={\frac {a}{2\sin \alpha }}={\frac {b}{2\sin \beta }}={\frac {c}{2\sin \gamma }}.}$

• Spojnice středu kružnice opsané a jednotlivých vrcholů trojúhelníka jsou kolmé k jednotlivým stranám jeho ortického trojúhelníka (tzv. Nagelova věta).
• Kružnice devíti bodů je stejnolehlým obrazem kružnice opsané se středem stejnolehlosti v těžiště trojúhelníka a koeficientem κ = - 0,5.
• Středem úsečky spojující střed kružnice opsané a Lemoinův bod je zároveň středem první Lemoinovy kružnice.

Kružnice opsaná trojúhelníku a její konstrukce

Kružnice opsaná a Simsonova přímka

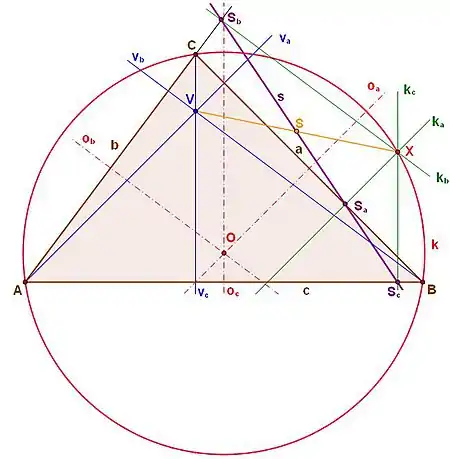
Pokud z libovolného bodu X kružnice opsané spustíme kolmice k jednotlivým stranám, paty kolmic leží na přímce. Nazývá se Simsonova přímka. Pokud tento bod X spojíme s ortocentrem (průsečík výšek trojúhelníka), pak Simsonova přímka prochází středem této úsečky. Simsonova přímka se jmenuje podle anglického matematika Roberta Simsona (1687-1768). Někdy se označuje také jako Wallaceova přímka.

Kružnice opsaná a Simsonova přímka:

• ABC
• a, b, c – strany
• o_a, o_b, o_c - osy stran,
• O – průsečík os stran (střed kružnice opsané),
• X – libovolný bod, ležící na kružnici opsané
• k_a, k_b, k_c – kolmice na strany, spuštěné z bodu X
• S_a, S_b, S_c – paty kolmic k_a, k_b, k_c
• s – Simsonova přímka
• v_a, v_b, v_c – výšky,
• V – průsečík výšek (ortocentrum)
• S – střed úsečky VX

Kružnice opsaná pravoúhlému trojúhelníku se nazývá Thaletova kružnice. Střed Thaletovy kružnice leží ve středu přepony trojúhelníku. Máme-li např. trojúhelník ABC, říkáme, že Thaletova kružnice je sestrojena nad průměrem AB.

Pro každou úsečku AB platí, že Thaletova kružnice sestrojená nad průměrem AB (s vyjmutím bodů A a B) je množinou vrcholů C všech pravoúhlých trojúhelníků ABC s přeponou AB.

Kartézské souřadnice středu opsané kružnice lze vypočíst podle vzorce

${\displaystyle {\begin{aligned}S_{x}&={\frac {1}{D}}\left[(A_{x}^{2}+A_{y}^{2})(B_{y}-C_{y})+(B_{x}^{2}+B_{y}^{2})(C_{y}-A_{y})+(C_{x}^{2}+C_{y}^{2})(A_{y}-B_{y})\right]\\S_{y}&={\frac {1}{D}}\left[(A_{x}^{2}+A_{y}^{2})(C_{x}-B_{x})+(B_{x}^{2}+B_{y}^{2})(A_{x}-C_{x})+(C_{x}^{2}+C_{y}^{2})(B_{x}-A_{x})\right]\end{aligned}}}$

přičemž pomocná hodnota D se vypočte

${\displaystyle D=2\left[A_{x}(B_{y}-C_{y})+B_{x}(C_{y}-A_{y})+C_{x}(A_{y}-B_{y})\right].\,}$

Indexy x a y označují x a y souřadnice vrcholů trojúhelníka (A,B,C) a středu kružnice S.