Thaletova věta
Thaletova věta je matematická věta o velikosti úhlů trojúhelníků vytvořených nad průměrem kružnice. Je pojmenována po Thalétovi z Milétu, který ji jako první dokázal.
Kružnice, která je součástí konstrukce Thaletovy věty, bývá označována jako Thaletova kružnice.
Znění
Všechny obvodové úhly sestrojené nad průměrem kružnice jsou pravé.
Jiné znění: Všechny trojúhelníky, jejichž nejdelší stranu půlí střed kružnice opsané, jsou pravoúhlé.
Nebo jinak: Sestrojme libovolnou kružnici s průměrem. Koncové body jejího průměru označíme A a B a zvolíme libovolný bod C na kružnici. Pak platí, že trojúhelník ABC je pravoúhlý a má pravý úhel u vrcholu C.
Původní znění[zdroj?!]: "Středový úhel je dvojnásobek obvodového" Z toho vyplývají předešlá znění. (Při středovém úhlu 180° - přímka je obvodový úhel pravý - 90°)
Důkaz
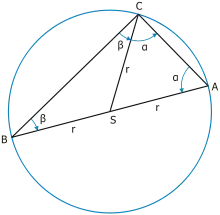
Na horním obrázku je příklad úhlu sestrojeného nad průměrem kružnice. Protože trojúhelníky CSB a ASC jsou rovnoramenné (vždy dvě z jejich ramen jsou dlouhá r), má úhel ∠BCA velikost α+β. Součet úhlů v trojúhelníku ABC je pak:
α + β + α + β = 2 α + 2 β = 180°.
Pokud poslední rovnost vydělíme dvěma, dostaneme, že úhel
∠BCA = α + β = 90°.
Geometrický důkaz
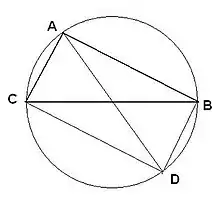
Bod A, vrchol trojúhelníku ABC, můžeme promítnout podle středové souměrnosti do bodu D, takže vznikne trojúhelník CBD. Strany čtyřúhelníka ABDC jsou po dvou rovnoběžné a obě jeho úhlopříčky (AD a CB) jsou průměry kružnice a tedy stejně dlouhé. Čtyřúhelník ABDC je tedy pravoúhlý a pravý je i úhel CAB.
Zobecnění
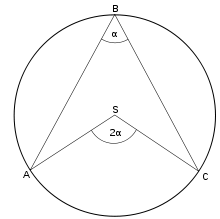
Thaletova věta je zvláštní případ věty: Jestliže máme tři body A, B a C na kružnici se středem S, potom úhel ∠ASC je dvakrát tak velký než úhel ∠ABC.
Historie
Thalés z Milétu nebyl první, kdo tuto větu vyslovil. Byla známá již Egypťanům a Babyloňanům, ačkoli ti ji znali jen ze zkušenosti, nedokázali ji. To udělal až Thalés, který využil znalostí toho, že úhly při základně rovnoramenného trojúhelníku mají stejnou velikost a součet úhlů v trojúhelníku je roven dvěma pravým úhlům.