Spojitá funkce
Spojitá funkce je taková matematická funkce, jejíž hodnoty se mění plynule, tedy při dostatečně malé změně hodnoty x se hodnota f(x) změní libovolně málo. Intuitivní (ne zcela přesná) představa spojité funkce spočívá ve funkci, jejíž graf lze nakreslit jedním tahem, aniž by se tužka zvedla z papíru. Funkce, která není spojitá, se označuje jako nespojitá.
.svg.png.webp)
Spojitost je také jednou ze základních vlastností běžně požadovaných po „rozumných funkcích“, mnoho matematických konstrukcí vyžaduje spojitost funkce jako nutnou podmínku – např. derivace, primitivní funkce apod.
Pro reálné funkce reálné proměnné lze spojitost funkce f v hromadném bodě definičního oboru x0 definovat následujícími dvěma podmínkami:
- Funkce je v bodě x0 definována (x0 patří do definičního oboru).
- V bodě x0 existuje limita funkce a je rovna právě funkční hodnotě v tomto bodě:
Tato definice mluví o spojitosti v bodě; mimo to se také používá výraz funkce spojitá na množině či intervalu (pokud je funkce spojitá ve všech bodech této množiny), obecně o spojité funkci se hovoří v případě, že je spojitá na celém svém definičním oboru.
Cauchyho definice
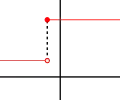 Funkce spojitá zprava
Funkce spojitá zprava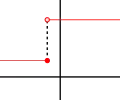 Funkce spojitá zleva
Funkce spojitá zleva
O funkci řekneme, že je spojitá v bodě a, pokud ke každému (libovolně malému) číslu existuje takové číslo , že pro všechna x, pro něž platí , platí také
- .
Velikost čísla může záviset nejen na volbě čísla , ale i na volbě bodu a.
Funkci označujeme jako spojitou zprava (resp. zleva), pokud k libovolnému existuje takové , že pro všechna (resp. ), tzn. pro všechna x z pravého okolí (resp. levého okolí) bodu , je . Funkce je spojitá tehdy, je-li spojitá zprava i zleva.
Cauchyho definici lze formulovat také pro funkci n proměnných. O funkci , kde jsou proměnné funkce, řekneme, že je spojitá v bodě , pokud ke každému (libovolně malému) číslu existuje takové číslo , že pro všechny body z okolí bodu A, tzn. pro body jejichž vzdálenost splňuje podmínku , platí
- .
Heineho definice
Nechť je hromadným bodem . Funkce je spojitá v bodě právě tehdy když platí .
Spojitost komplexní funkce
O komplexní funkci říkáme, že je spojitá, jestliže v daném bodě komplexní roviny platí
- .
Je-li funkce spojitá v každém bodě určité oblasti , pak říkáme, že je spojitá v .
Bod nespojitosti
Body, v nichž daná funkce není spojitá, označujeme jako body nespojitosti, singularity.
Za bod nespojitosti prvního druhu označíme takový bod , ve kterém má funkce limitu zprava i zleva, avšak tyto dvě limity mají rozdílné hodnoty, tzn. .[2] Rozdíl mezi těmito čísly, tzn. , nazýváme skokem funkce v bodě .[1]
Za bod nespojitosti druhého druhu označíme takový bod , v němž neexistuje alespoň jedna z vlastních (konečných) jednostranných limit.[2]
Pokud v bodě existuje vlastní (konečná) limita , avšak funkce není v bodě a definována, nebo je , pak bod označujeme jako odstranitelnou nespojitost funkce .[1]
Funkci, která je definována na intervalu , označíme jako po částech spojitou na daném intervalu, je-li spojitá ve všech bodech intervalu s výjimkou konečného počtu bodů, v nichž má nespojitost prvního druhu.

Na obrázku vpravo je bodem nespojitosti prvního druhu bod . Bod je bodem nespojitosti druhého druhu. Bod je odstranitelnou nespojitostí funkce f(x). Funkce je po částech spojitá na intervalu .
Stejnoměrná spojitost
Mějme funkci na intervalu , pro niž k libovolnému existuje takové, že pro libovolné dva body z intervalu splňující platí . Pak říkáme, že funkce je stejnoměrně spojitá na intervalu .
Weierstrassova věta
Weierstrassova věta říká, že libovolnou spojitou funkci na intervalu lze (s libovolnou přesností) aproximovat stejnoměrně v posloupností polynomů, tzn. k libovolnému existuje polynom takový, že pro všechna .
Absolutně spojitá funkce
Funkci označíme jako absolutně spojitou na intervalu , jestliže k libovolnému existuje takové , že pro každý systém intervalů pro který je , a platí .
Je-li funkce absolutně spojitá na intervalu , pak je na tomto intervalu spojitá a má na tomto intervalu konečnou variaci.
Příklady

- Všechny polynomické funkce, exponenciální funkce, sinus a kosinus a funkce absolutní hodnota jsou spojité v celém oboru reálných čísel.
- Racionální funkce, logaritmy, tangens a kotangens jsou spojité na svém definičním oboru (ale nejsou definované pro všechna reálná čísla).
- Funkce signum (znaménko) je nespojitá v bodě x = 0:
- I velmi malá změna hodnoty kolem tohoto bodu způsobí velkou změnu hodnoty: sgn −0,001 = −1, ale sgn 0,001 = 1.
- Funkce pro získání nejbližšího menšího celého čísla je nespojitá v každém celém čísle.
- Extrémním příkladem je tzv. Dirichletova funkce, která je definovaná pro všechna reálná čísla, ale v žádném bodě není spojitá.
Vlastnosti
- Má-li funkce v bodě konečnou derivaci, pak je v bodě a také spojitá.
- Pokud je funkce spojitá v bodě a funkce spojitá v bodě , pak složená funkce je spojitá v bodě .
- Je-li funkce spojitá na uzavřeném intervalu , pak na existuje alespoň jeden bod takový, že pro všechna Jedná se o maximum funkce na intervalu Současně také existuje alespoň jeden bod takový, že pro všechna . Jedná se o minimum funkce na intervalu . Funkce spojitá na uzavřeném intervalu je tedy na tomto intervalu také ohraničená.
Reference
- Matematika polopatě [online]. Nová média, c2006-2014 [cit. 2015-12-06]. Kapitola Spojitost funkce. Dostupné online.
- Math Tutor [online]. [cit. 2015-12-06]. Kapitola Spojitost reálných funkcí. Dostupné online.
Související články
- Funkce
- Komplexní funkce
- Spojité zobrazení
- Okolí
- Polospojitost
- Stejnoměrně spojitá funkce
- Absolutně spojitá funkce
- Lipschitzovská funkce
- Integrita
- Singularita