Riemannův integrál

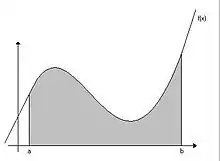Plocha pod grafem funkce

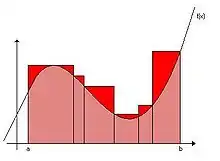Pokrytí celé plochy obdélníky pro horní součet

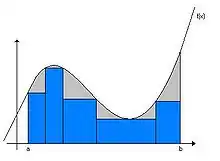Vložení obdélníků do plochy pro dolní součet

Definice Riemannova integrálu vychází z intuitivní představy měření obsahu plochy pod grafem funkce. Chceme-li přibližně zjistit tento obsah, provedeme to v praxi pravděpodobně tak, že položíme do měřené plochy nějaké geometrické útvary, jejichž obsah dovedeme spočíst, tak, aby nepřesahovaly hranici měřené oblasti a vzájemně se nepřekrývaly. Sečteme-li nyní obsahy všech vložených útvarů, dostaneme zřejmě číslo, které je menší než obsah měřené plochy — tzv. dolní odhad. Obdobně (pokrytím celé měřené plochy známými útvary) získáme tzv. horní odhad. Obsah měřené plochy pak leží mezi dolním a horním odhadem. Budeme-li používat k vykládání plochy stále menší a menší útvary, dokážeme oba odhady stále zpřesňovat, až teoreticky při vyložení plochy nekonečně mnoha nekonečně malými útvary dostaneme horní i dolní odhad roven stejnému číslu — obsahu měřené plochy. Pro jednoduchost se při zavádění Riemannova integrálu používají za ony útvary, jimiž se plocha vykládá, obdélníky se stranami rovnoběžnými s osami soustavy souřadnic.

Uvedeme dvě definice Riemannova integrálu. První definice pochází od Bernharda Riemanna. Druhá definice pochází od Gastona Darbouxe. Obě definice jsou ekvivalentní. To znamená, že funkce je integrovatelná podle Darbouxovy definice, právě když je integrovatelná podle Riemannovy definice a hodnota integrálu podle obou definic je shodná. Z Darbouxovy definice lze snadněji odvodit některé důležité vlastnosti Riemannova integrálu, proto se v literatuře vyskytuje častěji. Darbouxova definice vychází z úvahy naznačené v motivaci.
Obě definice využívají pojem dělení intervalu definovaný takto:

• Dělením ${\displaystyle D}$ intervalu ${\displaystyle \langle a,b\rangle }$ nazýváme (n+1)-tici ${\displaystyle t_{0},...,t_{n}}$ takovou, že ${\displaystyle a=t_{0}<t_{1}<...<t_{n}=b}$.

• Každá funkce, která je na daném intervalu po částech spojitá, je na tomto intervalu také integrovatelná.

• Mějme funkce ${\displaystyle f(x),g(x)}$ integrovatelné na intervalu ${\displaystyle \langle a,b\rangle }$. Pak platí

${\displaystyle \int _{a}^{b}[c_{1}f(x)+c_{2}g(x)]\mathrm {d} x=c_{1}\int _{a}^{b}f(x)\mathrm {d} x+c_{2}\int _{a}^{b}g(x)\mathrm {d} x}$,

kde ${\displaystyle c_{1},c_{2}}$ jsou konstanty. Na daném intervalu je tedy integrovatelná také funkce ${\displaystyle c_{1}f(x)+c_{2}g(x)}$.

• Integrovatelná je také funkce ${\displaystyle |f(x)|}$, přičemž platí

${\displaystyle \left|\int _{a}^{b}f(x)\mathrm {d} x\right|\leq \int _{a}^{b}|f(x)|\mathrm {d} x}$.

• Také funkce ${\displaystyle f(x)g(x)}$ je integrovatelná, avšak

${\displaystyle \int _{a}^{b}f(x)g(x)\mathrm {d} x\neq \int _{a}^{b}f(x)\mathrm {d} x\;\int _{a}^{b}g(x)\mathrm {d} x}$.

Pokud je funkce ${\displaystyle g(x)}$ na intervalu ${\displaystyle \langle a,b\rangle }$ kladná a zdola ohraničená nebo záporná a shora ohraničená, tedy ${\displaystyle 0>K\geq |g(x)|}$, pak je integrovatelná také funkce ${\displaystyle f(x)g(x)}$.

• Zvolíme-li na intervalu ${\displaystyle \langle a,b\rangle }$ bod ${\displaystyle c}$ takový, že ${\displaystyle a<c<b}$, pak lze psát

${\displaystyle \int _{a}^{b}f(x)\mathrm {d} x=\int _{a}^{c}f(x)\mathrm {d} x+\int _{c}^{b}f(x)\mathrm {d} x}$.

• Vzájemná záměna mezí intervalu, na němž integrujeme, vede ke změně znaménka integrálu, tzn.

${\displaystyle \int _{a}^{b}f(x)\mathrm {d} x=-\int _{b}^{a}f(x)\mathrm {d} x}$.

• Pokud pro všechna ${\displaystyle x\in \langle a,b\rangle }$ platí ${\displaystyle f(x)\geq 0}$, pak

${\displaystyle \int _{a}^{b}f(x)\mathrm {d} x\geq 0}$.

Pokud navíc alespoň v jednom bodě ${\displaystyle c\in \langle a,b\rangle }$, v němž je funkce ${\displaystyle f(x)}$ spojitá, platí také ${\displaystyle f(c)>0}$, pak

${\displaystyle \int _{a}^{b}f(x)\mathrm {d} x>0}$.

• Je-li funkce ${\displaystyle f(x)}$ na intervalu ${\displaystyle \langle a,b\rangle }$ spojitá a současně platí ${\displaystyle \int _{a}^{b}f^{2}(x)\mathrm {d} x=0}$, pak v celém intervalu ${\displaystyle \langle a,b\rangle }$ platí ${\displaystyle f(x)=0}$.

• Je-li na intervalu ${\displaystyle \langle a,b\rangle }$ ${\displaystyle f(x)\geq g(x)}$, pak platí také

${\displaystyle \int _{a}^{b}f(x)\mathrm {d} x\geq \int _{a}^{b}g(x)\mathrm {d} x}$.

• Je-li na intervalu ${\displaystyle \langle a,b\rangle }$ funkce ${\displaystyle f(x)}$ omezená, tzn. ${\displaystyle m\leq f(x)\leq M}$, kde ${\displaystyle m,M}$ jsou konstanty, a funkce ${\displaystyle g(x)\geq 0}$, pak platí nerovnosti

${\displaystyle m\int _{a}^{b}g(x)\mathrm {d} x\leq \int _{a}^{b}f(x)g(x)\mathrm {d} x\leq M\int _{a}^{b}g(x)\mathrm {d} x}$.

• Funkce ${\displaystyle f(x),g(x)}$, které jsou spojité na ${\displaystyle \langle a,b\rangle }$, splňují tzv. Schwarzovu nerovnost

${\displaystyle {\left(\int _{a}^{b}f(x)g(x)\mathrm {d} x\right)}^{2}\leq \int _{a}^{b}f^{2}(x)\mathrm {d} x\;\int _{a}^{b}g^{2}(x)\mathrm {d} x}$.

• Můžeme definovat funkci ${\displaystyle F(x)}$ proměnné ${\displaystyle x}$ vztahem

${\displaystyle F(x)=\int _{a}^{x}f(t)\mathrm {d} t}$.

Funkce ${\displaystyle F(x)}$ je spojitou funkcí proměnné ${\displaystyle x}$ a v každém bodě, v němž je ${\displaystyle f(x)}$ spojitá, má ${\displaystyle F(x)}$ derivaci, přičemž platí

${\displaystyle {\frac {\mathrm {d} F}{\mathrm {d} x}}={\frac {\mathrm {d} }{\mathrm {d} x}}\int _{a}^{x}f(t)\mathrm {d} t=f(x)}$.

• Podobně lze definovat funkci

${\displaystyle G(x)=\int _{x}^{b}f(t)\mathrm {d} t}$,

pro jejíž derivaci dostaneme

${\displaystyle {\frac {\mathrm {d} G}{\mathrm {d} x}}={\frac {\mathrm {d} }{\mathrm {d} x}}\int _{x}^{b}f(t)\mathrm {d} t=-f(x)}$.

• Pokud je funkce ${\displaystyle f(x)\geq 0}$ pro všechny body ${\displaystyle x\in \langle a,b\rangle }$, pak hodnota integrálu ${\displaystyle \int _{a}^{b}f(x)\mathrm {d} x}$ je rovna obsahu plochy, jejíž obvod tvoří osy ${\displaystyle x}$, funkce ${\displaystyle y=f(x)}$ a rovnoběžky s osou ${\displaystyle y}$, které mají rovnice ${\displaystyle x=a,x=b}$.

Je-li např. na intervalu ${\displaystyle \langle a,c\rangle }$ ${\displaystyle f(x)\geq 0}$ a na intervalu ${\displaystyle \langle c,b\rangle }$ ${\displaystyle f(x)\leq 0}$, pak plocha obrazce ohraničeného křivkou ${\displaystyle y=f(x)}$ není rovna hodnotě integrálu ${\displaystyle \int _{a}^{b}f(x)\mathrm {d} x}$, ale součtu integrálů ${\displaystyle \int _{a}^{c}f(x)\mathrm {d} x+\left|\int _{c}^{b}f(x)\mathrm {d} x\right|}$.

• Je-li funkce ${\displaystyle f(x)}$ spojitá na ${\displaystyle \langle a,b\rangle }$ a ${\displaystyle F(x)}$ je na tomto intervalu její libovolná primitivní funkce, pak platí (viz Newtonův integrál)

${\displaystyle \int _{a}^{b}f(x)\mathrm {d} x=F(b)-F(a)}$.

• Newtonův integrál
• Lebesgueův integrál
• Perronův integrál
• Stieltjesův integrál
• Kurzweilův integrál
• Křivkový integrál
• Plošný integrál

• Obrázky, zvuky či videa k tématu Riemannův integrál na Wikimedia Commons