Exponenciální funkce
Exponenciální funkce je matematická funkce ve tvaru
- ,
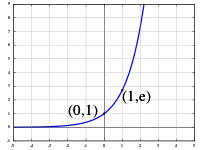
kde je kladné číslo různé od , které se nazývá základ. Číslu se říká exponent, grafem je exponenciála.
Definičním oborem exponenciální funkce jsou všechna reálná, resp. všechna komplexní čísla (a lze ji rozšířit i na složitější objekty, zejména lineární operátory).
Inverzní funkcí k exponenciále je logaritmus o stejném základu:
Derivací exponenciály je tato exponenciála vynásobená přirozeným logaritmem základu:
Protože přirozený logaritmus Eulerova čísla je rovný jedné, používá se toto číslo často jako základ exponenciální funkce. Derivace exponenciální funkce s tímto základem
je rovna opět exponenciální funkci o stejném základu . To přináší usnadnění při práci s výrazy obsahujícími exponenciálu. Proto se často pod označením exponenciální funkce automaticky myslí exponenciála se základem a exponenciály s obecným základem se převádějí na tento základ pomocí vzorce . Alternativní notace se používá, aby se exponent mohl zapsat na jeden řádek se zbytkem výrazu.
Formální definice
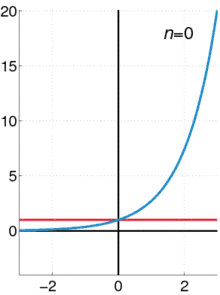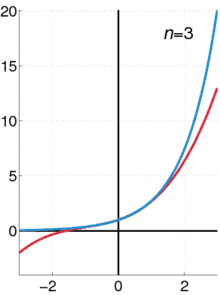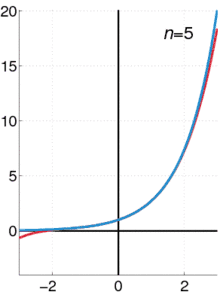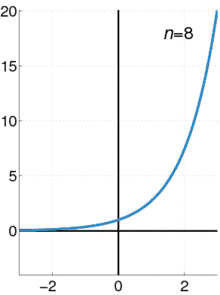
Exponenciální funkce ex může být charakterizována různými ekvivalentními způsoby. Zejména může být definována následující mocninnou řadou:
Méně často je ex definováno jako řešení y rovnice
- .
Lze ji definovat také následující limitou:
- .
Vlastnosti exponenciální funkce
Pro každou exponenciální funkci () platí:
- je zdola omezená
- je prostá
- je spojitá v každém bodě, ale není stejnoměrně spojitá na celém
- pro a > 1 je rostoucí, pro a ∈ (0; 1) klesající
- (tedy graf exponenciální funkce prochází bodem [0;1])
- ve speciálním případě .
Exponenciála o základu e
Často používaný základ exponenciální funkce je Eulerovo číslo . Funkce je až na násobek jediné řešení diferenciální rovnice
Funkce se obvykle definuje mocninnou řadou
která konverguje pro každé reálné i komplexní . Obecná exponenciální funkce se pak dá definovat jako
kde je přirozený logaritmus čísla .
Dosazením čistě imaginárního čísla do definice exponenciály dostáváme vztah
Derivace a diferenciální rovnice
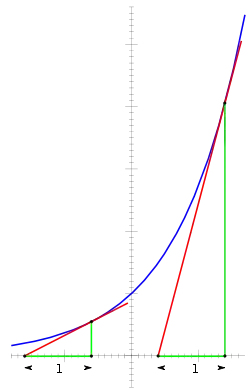
Důležitost exponenciální funkce v matematice a přírodních vědách pramení hlavně z vlastností její derivace, zejména:
Důkaz:
To znamená, že ex je svou vlastní derivací a tedy je jednoduchým příkladem pfaffovské funkce. Funkce tvaru cex (kde c je konstanta) jsou jediné funkce s touto vlastností (podle Picardovy–Lindelöfovy věty).
Tato vlastnost se dá vyjádřit i následujícími způsoby:
- Sklon grafu v libovolném bodě je hodnota funkce v tomto bodě.
- Tempo růstu funkce x je stejné jako hodnota funkce v bodě x.
- Funkce řeší diferenciální rovnici y′ = y.
- exp je pevný bod derivace.
Krom toho u diferencovatelné funkce f(x) používáme řetízkové pravidlo:
Vztah logaritmické a exponenciální funkce
Exponenciální a logaritmická funkce jsou navzájem inverzní, tedy platí:
- , .
Grafy těchto funkcí jsou osově souměrné podle přímky .
Řetězové zlomky pro
Řetězový zlomek pro ex lze získat prostřednictvím Eulerovy rovnosti:
Následující celkový řetězový zlomek pro ez konverguje mnohem rychleji:
nebo použitím substituce :
zvláštní případ pro z = 2:
Tento vzorec také konverguje, ale pomaleji, protože z > 2. Například:
Exponenciála operátorů
Mocninná řada v definici exponenciály umožňuje definovat exponenciálu i mnohem komplikovanějších objektů, než jsou komplexní čísla, zejména matic a operátorů. Mocniny a součty operátorů, respektive matic, jsou dobře definované a příslušná řada konverguje.
Komplexní rovina
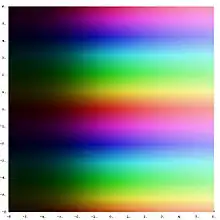
Stejně jako v reálném případě, exponenciální funkce může být definována na komplexní rovině několika ekvivalentními formami. Jedna taková definice je ekvivalentní definicí mocninnou řadou, kde je reálná proměnná nahrazena komplexní:
Exponenciální funkce je periodická s imaginární periodou 2πi a může být psána jako
- ,
kde a a b jsou reálné hodnoty a kde na pravé straně se vyskytují reálné funkce, pokud je tento předpis použit jako definice (Eulerův vzorec). Tento vzorec propojuje exponenciální funkci s goniometrickými a hyperbolickými funkcemi.
Uvažujeme-li funkci definovanou na komplexní rovině, pak exponenciální funkce zachovává tyto vlastnosti:
pro všechny z a w.
Exponenciální funkce je celá funkce neboť je holomorfní na celé komplexní rovině. Každé komplexní číslo kromě 0 má při exponenciální funkci svůj vzor; to znamená, že 0 je lacunární hodnota exponenciální funkce. Ilustruje tedy malou Picardovu větu, že jakákoli nekonstantní celá funkce má ve svém obrazu až na jeden bod celou komplexní rovinu.
Rozšířením přirozeného logaritmu do komplexních čísel získáme komplexní logaritmus log z, což je vícehodnotová funkce.
Pak můžeme definovat obecnou mocninu:
pro všechna komplexní čísla z a w. To je také vícehodnotová funkce, a to i když z je reálné. Tento fakt je poněkud problematický, neboť vícehodnotové funkce log z a zw lze lehce zaměnit s jejich jednohodnotovými ekvivalenty dosazením reálného čísla za z. Pravidlo o násobení exponentů v případě pozitivních reálných čísel musí být upraveno pro vícehodnotový kontext:
- (ez) w
≠ ezw, ale spíše (ez) w
= e(z + 2πin)w vícehodnotový po celých číslech n.
Exponenciální funkce zobrazuje každou přímku v komplexní rovině na logaritmické spirály v komplexní rovině se středem v počátku. Existují dva zvláštní případy: když původní přímka je rovnoběžná s reálnou osou, výsledná spirála se nikdy neuzavírá do sebe; a když původní přímka je rovnoběžná s imaginární osou, výsledná spirála je kruh o nějakém poloměru.
- Exponenciální funkce na komplexní rovině
 z = Re(ex + iy)
z = Re(ex + iy) z = Im(ex + iy)
z = Im(ex + iy)
Související články
Externí odkazy
 Obrázky, zvuky či videa k tématu exponenciální funkce na Wikimedia Commons
Obrázky, zvuky či videa k tématu exponenciální funkce na Wikimedia Commons