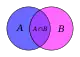
Symetrická diferencia
Symetrická diferencia alebo symetrický rozdiel dvoch množín je v teórii množín množina tých prvkov, ktoré patria práve do jednej z množín. Obsahuje teda všetky prvky z oboch množín, ktoré sa nenachádzajú v ich prieniku.[1]

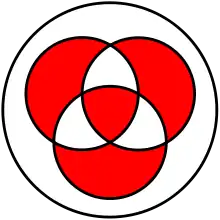
Symetrická diferencia množín A a B sa značí ako
alebo
- [chýba zdroj]
alebo
- [chýba zdroj]
Napríklad symetrická diferencia množín a je množina . Symetrická diferencia množín dievčat a študentov je množina všetkých dievčat, ktoré nie sú študentky a všetkých chlapcov študentov.
Vlastnosti
Symetrická diferencia je ekvivalentná so zjednotením oboch rozdielov množín:
a môže byť tiež vyjadrená ako zjednotenie dvoch množín bez ich prieniku:
alebo cez prvky pomocou logickej operácie XOR:
Z definície vyplýva, že symetrická diferencia je vždy (vlastnou alebo nevlastnou) podmnožinou zjednotenia množín:
pričom rovnosť v tejto neostrej inklúzii platí vtedy a len vtedy, ak a sú disjunktné množiny.
Symetrická diferencia je komutatívna a asociatívna:
Prienik je distributívny nad symetrickou diferenciou:
Prázdna množina je neutrálnym prvkom symetrickej diferencie a každá množina je svojím vlastným inverzným prvkom vzhľadom na symetrickú diferenciu:
Potenčná množina každej množiny sa teda stáva abelovskou grupou so symetrickou diferenciou ako operáciou a prázdnou množinou ako neutrálnym prvkom, kde neutrálny prvok a každý ďalší prvok grupy je svojím vlastným inverzným prvkom.[2]
Referencie
- SLEZIAK, Martin. 2-UMA-115 Teória množín [online]. Bratislava : Fakulta matematiky, fyziky a informatiky UK, 2011-11-16, [cit. 2018-07-22]. S. 27 – 29. Dostupné online.
- Symmetric difference [online]. PlanetMath, [cit. 2018-07-23]. Dostupné online.
Zdroj
Tento článok je čiastočný alebo úplný preklad článku Symetrická diference na českej Wikipédii.