Sekans

Sekans je goniometrická funkcia, ktorá každému reálnemu číslu $x$ , pre ktoré $\cos \;x\neq 0$ , priradí číslo $sec\;x={\frac {1}{\cos x}}$ , kde $x$ je uhol.
V pravouhlom trojuholníku sekans definujeme ako pomer dĺžky prepony a priľahlej odvesny. Pre označenie funkcie sa používa skratka sec. Funkcia sekans nie je často používaná, pretože sa dá zapísať pomocou funkcie kosínus.

Graf funkcie sekans

Hodnotu sekansu uhla x nemožno znázorniť jednotkovou kružnicou.
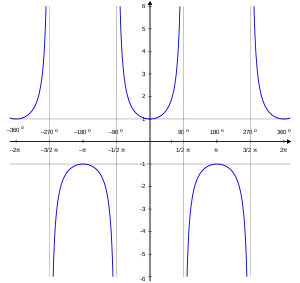
Opis priebehu funkcie sekans vyplýva z priebehu funkcie kosínus. Ak $x=0$ °, potom $\sec x=1$ . Keďže funkčné hodnoty funkcie $y=\cos x$ sú kladné, potom aj funkčné hodnoty funkcie y = sec x budú kladné. Funkcia bude v prvom kvadrante rastúca pretože funkcia y = cos x je v prvom kvadrante klesajúca. Pre x = 90° je cos x = 0, funkcia y = sec x nie je pre túto hodnotu definovaná. Čo sa týka druhého kvadrantu (90°;180°), funkčné hodnoty sú záporné a funkcia je rastúca, čo vyplýva z priebehu funkcie $y=\cos x$ . Pre x = 180° je sec x = -1. Funkčná hodnota -1 je najvyššia v celom druhom kvadrante. V treťom kvadrante je hodnota funkčných hodnôt záporná a funkcia je klesajúca. Pre x = 270° je cos x = 0 a preto funkcia y = sec x nie je v tomto bode definovaná. Vo štvrtom kvadrante je funkcia klesajúca a jej funkčné hodnoty sú kladné. Funkčné hodnoty nad osou x sú z intervalu $<1;\infty )$ a a pod osou x sú z intervalu $<-1;-\infty )$ . Z toho dôvodu obor funkčných hodnôt funkcie y = sec x je $R-(-1;1)$ .

Perióda funkcie kosínus je $2\pi$ , preto aj perióda funkcie sekans je $2\pi$ .

Vlastnosti

Funkcia $y=\sec x\,\!$ má nasledujúce vlastnosti (kde k je ľuboľné celé číslo):

Definičný obor: $\mathbb {R} -\left\{(2k+1)\cdot {\frac {\pi }{2}}\right\}$
Obor hodnôt: $\mathbb {R} -\left\{(-1;1)\right\}$
Funkcia je periodická s periódou $2\pi$
Funkcia je rastúca na každom intervale: $\left(2k\pi ;{\frac {\pi }{2}}+2k\pi \right){\text{ a }}\left({\frac {\pi }{2}}+2k\pi ;\pi +2k\pi \right)$

Funkcia je klesajúca na každom intervale: $\left(\pi +2k\pi ;{\frac {3\pi }{2}}+2k\pi \right){\text{ a }}\left({\frac {3\pi }{2}}+2k\pi ;2\pi +2k\pi \right)$
Funkcia je párna
Funkcia nie je nepárna
Funkcia nie je ohraničená
Pre túto funkciu neexistuje maximum ani minimum
Funkcia nie je spojitá pretože nie je definovaná pre $x=(2k+1)\cdot {\frac {\pi }{2}}$

Iné projekty

Commons ponúka multimediálne súbory na tému Sekans

Externé odkazy

Funkcia sekans

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

Goniometrické a súvisiace funkcie
Goniometrické funkcie	sínus kosínus tangens kotangens sekans kosekans historické sínus versus kosínus versus sínus koversus kosínus koversus exsekans exkosekans
Cyklometrické funkcie	arkussínus arkuskosínus arkustangens arkuskotangens arkussekans arkuskosekans
Hyperbolické funkcie	hyperbolický sínus hyperbolický kosínus hyperbolický tangens hyperbolický kotangens hyperbolický sekans hyperbolický kosekans
Hyperbolometrické funkcie	argument hyperbolického sínusu argument hyperbolického kosínusu argument hyperbolického tangensu argument hyperbolického kotangensu argument hyperbolického sekansu argument hyperbolického kosekansu