Cyklometrická funkcia
Cyklometrická funkcia je matematická funkcia inverzná ku funkciám goniometrickým.
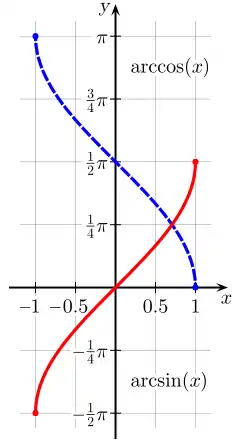
Arkus sínus a Arkus kosínus
Definícia
Medzi cyklometrické funkcie patria:
- Arkus sínus ()
- Arkus kosínus ()
- Arkus tangens ()
- Arkus kotangens ()
Aby mohla k ľubovoľnej funkcii existovať inverzná funkcia, daná funkcia musí byť prostá, to znamená: rôznym dvom prvkom musí priraďovať dve rôzne hodnoty. Goniometrické funkcie sú ale periodické, a teda nie sú prosté. Preto ak chceme uvažovať o cyklometrických funkciách musíme najskôr ošetriť ich definičný obor a taktiež aj definičné obory goniometrických funkcií – to znamená, že musíme vybrať len tú podmnožinu definičného oboru danej goniometrickej funkcie, na ktorej je prostá.
Definičné obory cyklometrických a goniometrických funkcií
| Goniometrické funkcie | Cyklometrické funkcie |
| Sínus: pre | Arkus sínus: pre |
| Cosínus: pre | Arkus cosínus: pre |
| Tangens: pre | Arkus tangens: pre |
| Cotangens: pre | Arkus cotangens: pre |
Vzťahy medzi cyklometrickými a goniometrickými funkciami
sin a arcsin
- , ak platí
- , ak platí
cos a arccos
- , ak platí
- , ak platí
tg a arctg
- , ak platí
cotg a arccotg
- , ak platí
Vzťahy medzi cyklometrickými funkciami
Pre platí
Pre platí
Vzťahy medzi cyklometrickými funkciami so vzájomne opačnými argumentmi
Súčty a rozdiely cyklometrických funkcií
arcsin x + arcsin y
- ak platí alebo
- ak platí
- ak platí
arcsin x - arcsin y
- ak platí alebo
- ak platí
- ak platí
arccos x + arccos y
- ak platí
- ak platí
arccos x - arccos y
- ak platí
- ak platí
arctg x + arctg y
- ak platí
- ak platí
- ak platí
arctg x - arctg y
- ak platí
- ak platí
- ak platí
arccotg x + arccotg y
- ak platí
- ak platí
arcsin x + arccos x
- ak platí
arctg x + arccotg x
Vyjadrenie cyklometrických funkcií v logaritmickom tvare
Cyklometrické funkcie sa dajú tiež vyjadriť použitím logaritmov a komplexných čísel:
Pozri aj
Literatúra
- Rektorys, K. a spol.: Přehled užité matematiky I., Prometheus, Praha, 2003, 7. vydání. ISBN 80-7196-179-5
- Bartch, Hans-Jochen: Matematické vzorce, SNTL, Praha 1987, 2. revidované vydání
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.