Matematická statistika

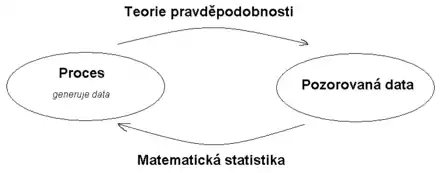
Matematická statistika je vědecká disciplína na pomezí popisné statistiky a aplikované matematiky. Zabývá se teoretickým rozborem a návrhem metod získávání a analýzy empirických dat obsahujících prvek nahodilosti, tedy teorií plánování experimentů, výběrů, statistických odhadů, testování hypotéz a statistických modelů. S využitím aparátu teorie pravděpodobnosti se snaží odhadnout vlastnosti rozdělení pozorovaných dat, chápaných jako realizace náhodných veličin, a metodologicky plánovat sběr dat tak, aby toto odhadování bylo efektivní. Jestliže tedy teorie pravděpodobnosti na základě znalosti chování určité náhodné veličiny určuje pravděpodobnost určitého výsledku (náhodného pokusu), matematická statistika naopak na základě dat hledá vlastnosti náhodné veličiny. Tento postup se označuje jako statistická inference, statistická indukce nebo statistické usuzování. Základními typy statistické inference jsou bodový odhad, intervalový odhad a testování hypotéz. Jako statistické modelování se označuje tvorba a testování komplexních hypotéz o datech, zahrnující obvykle určování více parametrů či složitou strukturu dat.

Teorie pravděpodobnosti popisuje vznik náhodných dat, zatímco matematická statistika usuzuje z dat na charakter procesů, jimiž data vznikla

Matematická statistika se vyvíjela paralelně s teorií pravděpodobnosti. První netriviální postupy tohoto oboru byly známy již v 18. století. Na počátku 19. století Carl Friedrich Gauss a Adrien-Marie Legendre vynalezli metodu nejmenších čtverců a na konci tohoto století a na počátku 20. století se matematické metody statistiky začaly rychle rozvíjet v souvislosti s eugenickým a biologickým výzkumem. Vlastním tvůrcem matematické statistiky jako samostatné disciplíny v dnešním pojetí byl v první polovině 20. století britský biolog Ronald Fisher. Od té doby se matematická statistika bouřlivě rozvíjí a její metody se používají ve všech empirických vědách při získávání a interpretaci dat.

Historie
Nejstarší statistický test
Nejstarší doložený příklad statistického testu je článek An Argument for Divine Providence,[1] který roku 1710 uveřejnil John Arbuthnot. Z dat londýnských matrik za roky 1629–1710 Arbuthnot zjistil, že v každém z těchto 82 let bylo pokřtěno více chlapců než dívek. Kdyby se rodilo zhruba stejně chlapců jako dívek, bylo by to, jako by v 82 hodech mincí pokaždé padl orel. Pravděpodobnost takového jevu je , což se přibližně rovná 1 / 4 836 000 000 000 000 000 000 000. Arbuthnot tak nepravděpodobnou možnost zavrhl (moderním jazykem řečeno zamítl nulovou hypotézu stejné pravděpodobnosti narození chlapce jako dívky) a prohlásil, že chlapců se prostě rodí více.

Článek měl ambice více filosofické a morální a objev testu je tak spíše vedlejší produkt – Arbuthnot ze svého výpočtu odvodil, že vzhledem k vyšší úmrtnosti mužů je jím dokázaný jev projevem péče božské Prozřetelnosti o lidstvo. Bůh se tak stará, aby na jednoho muže v dospělosti připadala jedna žena, což zároveň svědčí o nepřirozenosti a škodlivosti polygamie.[2]

Některé prvky matematické statistiky se objevily již v 17. a 18. století. Šlo zejména o vyrovnávací počet, který začal pro účely astronomie používat již Galileo Galilei a pro účely geodetických měření rozvinul Roger Boscovich. Již v roce 1710 uveřejnil John Arbuthnot první článek, v němž byl použit statistický test, význam tohoto myšlenkového postupu však ještě dlouho poté unikal pozornosti přírodovědců.[3] V tomto období byly také položeny základy teorie pravděpodobnosti. Mezi zakladatele této disciplíny patří Pierre de Fermat, Blaise Pascal a Christiaan Huygens v 17. století, Jacob Bernoulli, Abraham de Moivre, Thomas Bayes a Pierre Simon de Laplace ve století 18. Bayes a Laplace započali teorii induktivního pravděpodobnostního uvažování, jež je základem dnešního bayesovského přístupu ke statistice, nazvaného na počest prvního z nich.[4]

19. století přineslo další rozvoj metod teorie pravděpodobnosti a rodící se matematické statistiky. Na jeho počátku byla objevena metoda nejmenších čtverců. Zřejmě ji použil Carl Friedrich Gauss již roku 1801 při výpočtu dráhy planetky Ceres, ale poprvé byla uveřejněna roku 1805 Legendrem, který ji objevil nezávisle na Gaussovi.[5] V tomto století se také metody matematické statistiky začaly z fyzikálních věd šířit i do oblasti věd biologických a humanitních. Adolphe Quételet je aplikoval na demografii, Gustav Fechner využil pro psychologické experimenty a Francis Galton v rámci svých studií dědičnosti zavedl pojem korelace a objevil regresi k průměru, z níž pak vznikl název regresní analýza. Charles Sanders Peirce v pojednáních Illustrations of the Logic of Science (1877–1878) a A Theory of Probable Inference (1883) formuloval mnohé základní prvky matematické statistiky, zejména položil základy teorie testování hypotéz a randomizovaných experimentů. Testování hypotéz na přelomu 19. a 20. století rozvíjeli Karl Pearson (chí-kvadrátový test) a William Sealy Gosset, známý pod pseudonymem Student (t-test).[6]

Vlastním zakladatelem moderní matematické statistiky jako disciplíny se stal britský biolog Ronald Fisher.[7] Napsal vlivné učebnice Statistical Methods for Research Workers (1925) a The Design of Experiments (1935) a objevil či podstatně prohloubil celou řadu klíčových metod a pojmů jako jsou analýza rozptylu, metoda maximální věrohodnosti, diskriminační analýza, informace a plánování experimentů.

Kolem poloviny 20. století se matematická statistika stala samostatným oborem na pomezí čisté a aplikované matematiky, který se rozvíjí řadou směrů. Teorii statistických dat, experimentálního designu a výběru obohatili například William Gemmell Cochran, Leslie Kish, C. R. Rao a Donald Rubin. Frank Hampel, Peter J. Huber, John Tukey a další badatelé rozvíjeli robustní metody odhadů a exaktní statistické metody, jež jsou málo citlivé k extrémním hodnotám v datovém souboru a platné i pro malé rozsahy výběrů. V návaznosti na klasické Thurstonovy a Guttmanovy práce vznikla teorie a metodologie statistického škálování, k níž přispěli například Clyde H. Coombs, Roger N. Shepard, Joseph B. Kruskal a rovněž Lee J. Cronbach teorií reliability škál. Analýzu kategorizovaných dat obohatil Leo A. Goodman metodologií logaritmickolineárních modelů.

Inspirace z oblasti sociálních věd přinesla například rozpracování metod z okruhu faktorové analýzy, jejíž základy položili psychologové Charles Spearman a Raymond Cattell a později rozpracovali Karl G. Jöreskog a Dag Sörbom, dále teorie latentních tříd, kterou navrhl sociolog Paul Felix Lazarsfeld, či teorie rozhodovacích stromů, u jejíchž kořenů stojí sociologové William A. Belson a James N. Morgan. V oblasti ekonomie a ekonometrie působili například Harold Hotelling (kanonická korelační analýza) nebo James Tobin (regrese cenzorovaných dat). Významná pro ekonomii je rovněž statistická analýza časových řad, k níž přispěli například George Box, Gwilym Jenkins či Tim Bollerslev, a analýza přežití, kterou rozvinuli mimo jiné Edward L. Kaplan, Paul Meier a David Cox. Použití metod matematické statistiky v průmyslu je spojeno se jmény Waltera A. Shewharta a W. Edwardse Deminga, kteří se stali zakladateli metodologie a hnutí řízení kvality. Rychle stoupá význam metaanalýzy, metodologie umožňující kombinovat výsledky většího množství nezávislých empirických studií; ze statistiků k její teorii přispěli například Nambury S. Raju, Larry V. Hedges, John E. Hunter, Jacob Cohen či Thomas C. Chalmers.

Nástup počítačů v polovině 20. století se projevil usnadněním rozsáhlých výpočtů, které s sebou matematická statistika přináší, a umožnil i vznik takzvaných výpočetně náročných metod ve statistice, často založených na myšlence algoritmu Monte Carlo, tedy opakovaném generování náhodných jedinců ze zkoumané populace. To také koncem 20. století umožnilo rychlý nástup bayesovských metod, které sice již dříve propagovali například Harold Jeffreys nebo Edwin Thompson Jaynes, ale které byly zhruba až do sedmdesátých let limitovány jak nedostatečnou výpočetní silou počítačů, tak i nepřítomností numerické metodologie, která by umožnila odhadnout složité integrály vznikající při jejich nasazení. Dalším aspektem rozšíření počítačů byl rozvoj programového vybavení pro matematickou statistiku. Zejména nástup univerzálních programových balíků od 60. let 20. století umožnil uživatelsky příjemným způsobem masově aplikovat výsledky vědecké práce v tomto oboru.

Data a jejich získávání

Statistická data, v dnešní době dostupná obvykle v podobě počítačových databází, se dají zkoumat z různých hledisek.


Data především mohou být úplná a zahrnovat celou základní populaci (čili základní soubor), tedy všechny objekty našeho zájmu. Častěji však máme k dispozici jen jejich podmnožinu, zvanou ve statistice výběr, výběrový soubor, výběrová populace či vzorek.[8] Počet objektů v této podmnožině se označuje a nazývá rozsah výběru. Postupy získávání výběru zkoumá teorie výběru, která se zabývá mimo jiné tím, zda je výběr reprezentativní, tedy zda popisné charakteristiky výběru se až na náhodnou výběrovou chybu shodují s charakteristikami celé základní populace. Základním způsobem dosahování reprezentativnosti přitom jsou různé druhy pravděpodobnostního výběru, při nichž má každý prvek základní populace známou nenulovou pravděpodobnost, že bude obsažen ve vzorku. Není-li výběr reprezentativní, vzniká systematická chyba, která znemožňuje korektní zobecnění výsledků analýzy na celou základní populaci.[9] Často však není pravděpodobnostní výběr možný a jsou k dispozici např. pouze data vzniklá „na základě příležitosti“ (oportunitní), o jejichž reprezentativnosti není jasno – to se týká např. mnoha situací v astronomii nebo historických vědách. V takovém případě je k zobecnění potřeba přistupovat s velkou opatrností.

Zkoumají-li se kauzální závislosti, tedy vliv různých zásahů, používá se experimentální design. Například některé náhodně vybrané prvky populace mohou být podrobeny zásahu, jejíž efekt se zkoumá, zatímco zbylé slouží jako kontrolní skupina. Rozdíl mezi ošetřenou a kontrolní skupinou pak lze až na výběrovou chybu interpretovat jako vliv zásahu.[10] Do designu vytváření a sběru dat se může promítnout i čas, takže hovoříme o časových řadách a longitudinálních studiích.

Data obsahují hodnoty sledovaných znaků (či – z hlediska datového souboru – proměnných), což mohou být hodnoty jak numerické (např. délka života pacienta po operaci), tak i nenumerické, kategoriální (např. umístění nádoru v těle). Podle toho, jakou interpretaci numerická data mají, tj. zda je např. lze pouze seřadit, nebo zda je lze i sčítat, hovoří se pak ještě o měřítku proměnné čili typu škály.[11] Zvláštním problémem analýzy jsou chybějící údaje – data, která nebyla zjištěna, ztratila se anebo nejsou smysluplně definována.

Explorační analýza

Explorační analýza dat (Exploratory data analysis, EDA) je souhrn metod používaných pro průzkum dat a hledání hypotéz, které stojí za to testovat (testování se v tomto kontextu označuje jako konfirmační analýza). Explorační analýzu etabloval jako samostatný podobor statistiky John Tukey.[12] Hlavní úkoly explorační analýzy dat jsou:

  • Navrhnout hypotézy o příčinách pozorovaných jevů.
  • Ověřit předpoklady statistických metod, které se použijí.
  • Podložit výběr vhodných statistických nástrojů a technik.
  • Poskytnout základnu dalšímu sběru dat pomocí průzkumů či experimentů.

Statistická inference

Základní úlohou matematické statistiky je zobecnění (zvané v tomto oboru statistická inference, statistická indukce či statistické usuzování): zkoumá se, jak informace zjištěné o prvcích výběru zobecnit na celou populaci.[13] Používané metody se opírají o zákon velkých čísel a příbuzné věty teorie pravděpodobnosti, jako je například Glivenkova-Cantelliho věta; ty ukazují, že při rostoucím rozsahu reprezentativního výběru se výběrové odhady obvykle limitně blíží skutečným hodnotám na celé populaci. Matematická statistika zároveň stanovuje, jak přesný tento odhad pro daná data je (intervalový odhad), anebo testuje, zda vlastnosti vzorku jsou slučitelné s předpoklady o chování celé populace (testování statistických hypotéz).

Odhady
Příklad: Bodový odhad střední hodnoty
Střední hodnota reálné náhodné veličiny X s hustotou pravděpodobnosti p(x) se určí jako

Tento integrál nelze přesně vypočítat z dat výběru xi (tedy z konečného počtu realizací náhodné veličiny X), ale lze ho aproximovat výběrovým průměrem počítaným podle vztahu

.

Jsou-li splněny předpoklady zákona velkých čísel, konverguje tato aproximace k EX s rostoucím rozsahem výběru n.

Číslo definované jako funkce distribuce nějaké náhodné veličiny se označuje jako statistický funkcionál či statistika. Příkladem statistiky je střední hodnota nebo rozptyl. Často je třeba z dat o výběrové populaci odhadnout hodnotu statistiky na základní populaci. Tato úloha se označuje odhad. Nejjednodušším přístupem je vypočítat vhodný bodový odhad, tedy jedno číslo, které co nejlépe aproximuje hledaný statistický funkcionál.

Sám o sobě však bodový odhad obvykle nestačí, protože neposkytuje žádnou představu o přesnosti získané aproximace. Proto se počítá intervalový odhad, jehož výsledkem je interval spolehlivosti (konfidenční interval), tedy interval, v němž se s jistou předem zadanou pravděpodobností nachází hodnota hledané statistiky základní populace. Výsledek se pak často udává ve formě

bodový odhad ± polovina šířky intervalu spolehlivosti.[14]

V bayesovském přístupu ke statistice se namísto konfidenčního intervalu zjišťuje distribuce zkoumané statistiky podmíněná daty výběrové populace.[15]

Testování hypotéz

Testování hypotézy je postup, který umožňuje na základě naměřených dat určit, zda náhodná veličina, jejímiž realizacemi data jsou, vykazuje určitou vlastnost. Například lze testovat, zda se střední hodnota náhodné veličiny liší od dané konstantní hodnoty – praktickou aplikací takového testu by mohlo být, zda je soustruh dobře seřízen a střední hodnota průměru jím vyráběných součástek se rovná hodnotě předepsané výkresem. V takovém případě je možné použít jednovýběrový t test, jsou-li rozměry součástek normálně rozděleny.

Testování může zahrnovat i více proměnných. Příkladem může být test toho, zda se navzájem liší střední hodnota náhodné veličiny X ve skupinách definovaných diskrétní náhodnou veličinou Y – takovýto test může být užitečný například v situaci, kdy X je výnos jabloní a Y je značka hnojiva, kterým se stromy ošetřují, takže test zjišťuje, zda se účinky jednotlivých hnojiv od sebe statisticky významně liší. V tomto případě lze při testování využít analýzu rozptylu, jsou-li splněny předpoklady této metody.

V klasické teorii testování se vychází z toho, že platí předpokládaná vlastnost zkoumaných náhodných veličin. Tento předpoklad se označuje nulová hypotéza a značí . Jelikož data jsou náhodná a náhoda může „pracovat proti nám“, nelze obvykle závěry testování vyslovit s naprostou jistotou. Proto se zároveň se předem stanoví hladina spolehlivosti , což je míra rizika (pravděpodobnost) toho, že hypotézu zamítneme, ačkoliv ve skutečnosti platí (omyl označovaný jako chyba 1. druhu). Hladina spolehlivosti se tradičně stanovuje 0,05 nebo 0,01. Menší hladina spolehlivosti znamená větší jistotu při zamítání nulové hypotézy, ale zároveň také větší riziko chyby 2. druhu, jež spočívá v akceptování nulové hypotézy, ačkoli tato hypotéza ve skutečnosti neplatí.

Dále se z dat vypočítá takzvané testovací kritérium, jehož rozdělení podmíněné předpokládanou platností nulové hypotézy je známo. Vyjde-li hodnota testovacího kritéria typická pro toto známé rozdělení, nulovou hypotézu akceptujeme či přesněji řečeno nezamítáme na základě známých dat. Naopak vyjde-li hodnota extrémní, tedy v oblasti hodnot, do níž realizace předpokládaného rozdělení padají s pravděpodobností menší než (tj. hodnota testovacího kritéria překročí kritickou mez), usoudíme, že testovací kritérium nejspíše nepochází z předpokládaného rozdělení a nulovou hypotézu zamítneme ve prospěch opačné tzv. alternativní hypotézy, označované .

Zatímco dříve bylo třeba hledat kritické meze v tabulkách rozdělení příslušného testovacího kritéria, dnes statistické softwary vypisují takzvanou hodnotu významnosti (též zvanou signifikance, p-hodnota nebo hladina významnosti). Tato hodnota udává pravděpodobnost, že při platnosti nulové hypotézy vyjde testová statistika rovna naměřené nebo ještě extrémnější. Test se vyhodnocuje takto:

  • Je-li hodnota významnosti menší než hladina spolehlivosti (), pak zamítneme nulovou hypotézu a přijmeme alternativní hypotézu. Riskujeme chybu prvního druhu s pravděpodobností nanejvýš .
  • Je-li hodnota významnosti větší nebo rovna než hladina spolehlivosti (), pak nulovou hypotézu nezamítneme. Riskujeme chybu druhého druhu s pravděpodobností označovanou .[16]

Bayesovský přístup ke statistice podobné úlohy pojímá jako problém stanovení distribuce zkoumané vlastnosti, podmíněné daty a naší výchozí informací o zkoumaném systému.[17] V příkladech uvedených na počátku odstavce by to byla distribuce střední hodnoty rozdělení průměrů součástek resp. distribuce středních hodnot výnosů ve skupinách podle použitého hnojiva.

Modelování
Lineární regrese: červeně jsou data (dvojice x, y), modře lineární regresní funkce, zeleně rezidua

Statistické modelování znamená snahu pomocí zjištěných dat pochopit mechanismus, jakým data mohla vzniknout. Jako model se tedy chápe rozdělení pravděpodobnosti, z něhož mohla vzniknout zkoumaná empirická data. Pro účely modelování se data obvykle chápou jako složená ze signálu, to jest deterministické složky, a šumu:

data = signál + šum.

Data se modelují jako složená z nějaké známé deterministické matematické funkce a reziduální hodnoty, která se chová jako nedeterministický šum – neobsahuje žádnou nebo jen malou systematickou informaci:

data = deterministická funkce + náhodné reziduum.

Funkce, deterministická složka modelu, závisí na externích proměnných (nezávisle proměnných) a u časových řad případně i na starších hodnotách naměřených dat.

Model tedy má aproximovat deterministickou (nenáhodnou) složku dat, odhadnout velikost a typ šumu a pomoci pochopit, jak modelovaná data vznikla resp. jak lze jejich hodnoty ovlivňovat vstupními proměnnými. Matematická funkce, která je první složkou modelu, často obsahuje parametry, které je třeba odhadnout z dat tak, aby model co nejlépe vystihl data (parametrické modelování). Zvláštními testy se zkoumá kvalita modelu a provádí se jeho interpretace.[18]

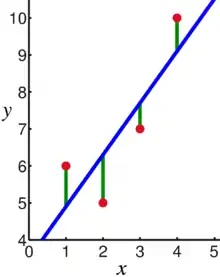
Nejjednodušší statistické modely jsou obsaženy již v základech odhadu a testování hypotéz. Například odhad výběrového průměru a jeho konfidenčního intervalu implikuje model dat jakožto součtu konstanty (střední hodnoty) a gaussovské náhodné veličiny (jejíž rozptyl ovlivňuje šířku konfidenčního intervalu). Jako modely ve vlastním smyslu se však označují složitější případy, závislé na více různých parametrech či komplexnějších pravděpodobnostních schématech. Historicky nejstarším a často používaným příkladem složitějšího statistického modelu je lineární regrese. V základní podobě její tvar vypadá takto:

hodnoty závisle proměnné y = lineární funkce nezávisle proměnné x + reziduum s normálním rozdělením,

což se přesněji a stručněji vyjádří takto:

kde y je reálná závisle proměnná (vysvětlovaná proměnná), x je reálná nezávisle proměnná (vysvětlující proměnná, prediktor), i označuje pořadové číslo pozorování, realizaci normálně rozložené náhodné veličiny (reziduum, které modeluje šum) a parametry a, b určují tvar lineární funkce: a má význam směrnice přímky a b je úsek na ose y. Základním úkolem tohoto typu regresní analýzy je oba parametry odhadnout, například metodou nejmenších čtverců.[19]

Kohonenova síť znázorňující hlasování členů Kongresu USA o některých zákonech (červená je „ano“, modrá „ne“). Výjimky jsou obrázek vlevo nahoře, ukazující členství ve straně (červená jsou republikáni, modrá demokraté), a jeho soused znázorňující vzdálenosti mezi uzly sítě.

Regresní modelování je možno zobecnit například připuštěním nelineárních vazeb mezi proměnnými nebo zavedením většího množství nezávisle proměnných. Zobecněný lineární model (generalized linear model, GLM) zahrnuje celou řadu těchto zobecnění; vedle něho pak existují další nelineární modely, například některé typy neuronových sítí nebo rozhodovací stromy. Dále existuje celá řada specializovaných regresních modelů zejména v analýze časových řad, například modely ARIMA a GARCH.[20]

Odhadování parametrů modelů se v jednoduchých případech, jako je lineární regrese, děje přímým výpočtem založeným na kalkulu rozdělení pravděpodobností. Složitější modely obvykle neumožňují najít vzorec pro přímý výpočet optimálních hodnot parametrů, a proto se používá celá řada přibližných numerických postupů, například metoda maximální věrohodnosti, různé varianty hladového algoritmu nebo simulační algoritmy typu Monte Carlo.

Vedle regresního modelování, kde je k dispozici závisle proměnná, existují i modely, které hledají strukturu zjištěných dat a dělení závisle a nezávisle proměnné nepoužívají. Příklady takového přístupu jsou například shluková analýza (též zvaná seskupovací analýza či matematická taxonomie), faktorová analýza nebo Kohonenovy neuronové sítě (self-organizing map, SOM). Cílem je zde například jednotlivé objekty či proměnné rozdělit do skupin (shluků, kategorií, taxonů, segmentů...) tak, aby v každé skupině byly objekty sobě podobné, a naopak objekty z různých skupin si podobné nebyly.

V bayesovském paradigmatu se parametrické modelování chápe jako výpočet či odhad rozdělení pravděpodobnosti parametrů podmíněné zjištěnými daty, tedy

kde jsou parametry a symbolizuje data. Pomocí Bayesovy věty se tato pravděpodobnost dá až na normující koeficient rozepsat jako

kde značka vyjadřuje přímou úměrnost, je pravděpodobnost, že daná data vzniknou, podmíněná hodnotami parametrů modelu, a je apriorní pravděpodobnost hodnot parametrů, zjednodušeně řečeno analytikovo očekávání jejich hodnoty předtím, než začal sbírat data. Výraz je obecným zápisem modelu jakožto rozdělení pravděpodobnosti. Vzorec tak poskytuje přímý návod, jak určit distribuci parametrů na základě známých dat, navrženého modelu a apriorního očekávání o parametrech.

Bayesovské východisko umožňuje konceptuálně jednotný a jednoduchý přístup k celé oblasti statistického modelování, na druhou stranu často vede k výpočetně velmi náročným úlohám, které bylo možno zvládnout až s nástupem rychlých počítačů a s objevem speciálních metod pro odhadování složitých integrálů jako je MCMC (Markov chain Monte Carlo).[21]

Aplikace

Metody matematické statistiky pronikly během 20. století prakticky do všech empirických vědních disciplín a do mnoha těch, které bývají řazeny k humanitním vědám. Raný vývoj oboru je spojen s aplikacemi v biologii, psychologii a dalších přírodních vědách. Teorie návrhu a vyhodnocování experimentů nebo výběrových šetření však brzy přesáhla i do jiných oblastí. Významný vliv mají statistické metody v teorii měření[22] a některých oblastech matematické fyziky, zejména statistické fyziky[23]. O statistické metody se opírá moderní matematická lingvistika[24], demografie, ekonometrie[25] a pojistná matematika[26] stejně jako epidemiologie či biostatistika[27]. Obchodní i přírodovědné aplikace mají robotika[28], data mining[29] či zpracování signálu[30], v nichž se matematická statistika propojuje s informatikou a dalšími obory. V inženýrské oblasti se používají teorie řízení[31], řízení kvality[32], teorie spolehlivosti[33] a teorie hromadné obsluhy[34], které rovněž podstatně využívají poznatky matematické statistiky.

Programové vybavení

Moderní matematická statistika je zejména ve své aplikované části závislá na počítačové technice. Vedle obecných softwarových systémů pro symbolické výpočty (např. Mathematica) či řešení numerických problémů (např. MATLAB) existuje celá řada specializovaných programů. Programovací jazyk S a nyní zejména jeho zdarma dostupný klon R se staly významnými nástroji pro rozvoj a šíření metod statistické analýzy dat. Širokou sadu obvyklých procedur s většinou uživatelsky příjemným ovládáním obsahuji komerční programové balíky jako je SPSS firmy IBM, SAS System firmy SAS Institute, Statistica firmy StatSoft a mnoho dalších. Tyto balíky navíc obvykle obsahují i skriptovací programovací jazyky, které uživatelům umožňují implementovat specifické postupy neobsažené v základní sadě procedur příslušného balíku. Kromě toho existuje a v řadě případů se dá stáhnout na internetu řada speciálních jednoúčelových programů, které jsou často vytvořeny matematickými statistiky jako implementace jimi objevených testů a algoritmů.[35]

Reference
  1. John Arbuthnot: An Argument for Divine Providence. canoe.ens.fr [online]. [cit. 2009-05-16]. Dostupné v archivu pořízeném dne 2013-10-24.
  2. DAVID, H.A.; EDWARDS, A.W.F. Annotated Readings in the History of Statistics. New York: Springer, 2001. ISBN 978-0387988443. (anglicky), s 7–18.
  3. STIGLER, Stephen M. The History of Statistics: The Measurement of Uncertainty before 1900. Harvard: Belknap Press of Harvard University Press, 1990. ISBN 978-0674403413. (anglicky) (dále Stigler 1990), s. 225
  4. Stigler 1990, s. 99–138
  5. Stigler 1990, s. 55–61
  6. Stigler 1990, s. 263–361
  7. HALD, Anders. A History of Mathematical Statistics from 1750 to 1930. [s.l.]: Wiley-Interscience, 1998. ISBN 978-0471179122. (anglicky)
  8. HENDL, Jan. Přehled statistických metod zpracování dat. Praha: Portál, 2004. ISBN 80-7178-820-1. (dále Hendl 2004), s. 37–38.
  9. Hendl 2004, s. 39
  10. Hendl 2004, s. 59–76
  11. Hendl 2004, s. 43–46
  12. Tukey, John Wilder (1977). Exploratory Data Analysis. Addison-Wesley. ISBN 0-201-07616-0.
  13. Hendl 2004, s. 18
  14. Hendl 2004, s. 166–175
  15. GELMAN, Andrew a kol. Bayesian Data Analysis. Boca Raton: Chapman & Hall / CRC, 2004. ISBN 1-58488-388-X. (dále Gelman 2004), s. 6–9.
  16. Hendl 2004, s. 175–179
  17. Gelman 2004, s. 4–5
  18. Hendl 2004, s. 80–81
  19. Hendl 2004, s. 266–279
  20. HAMILTON, James D. Time Series Analysis. Princeton: Princeton University Press, 1994. ISBN 0-691-04289-6.
  21. Gelman 2004, s.283–309.
  22. SHULTZ, Kenneth S.; WHITNEY, David J. Measurement Theory in Action: Case Studies and Exercises. Thousand Oaks: Sage Publications, 2004. Dostupné online. ISBN 978-0761927303. (anglicky)
  23. MANDL, Franz. Statistical Physics. Chichester: Wiley, 1988. ISBN 978-0471915331. (anglicky)
  24. WOODS, Anthony; FLETCHER, Paul; HUGHES, Arthur. Statistics in Language Studies. Cambridge: Cambridge University Press, 1988. ISBN 978-0521273121. (anglicky)
  25. KENNEDY, Peter. A Guide to Econometrics. Malden: Blackwell, 2008. ISBN 978-1405182577. (anglicky)
  26. PROMISLOW, S. David. Fundamentals of Actuarial Mathematics. Chichester: Wiley, 2006. Dostupné online. ISBN 978-0470016893. (anglicky)
  27. JEKEL, James F.; KATZ, David L.; ELMORE, Joann G. Epidemiology, Biostatistics and Preventive Medicine. Philadelphia, Penn: Saunders, 2001. Dostupné online. ISBN 978-0721690797. (anglicky)
  28. RUSSEL, Stuart; NORVIG, Peter. Artificial Intelligence: A Modern Approach. Upper Saddle River, NJ: Prentice Hall, 2002. ISBN 978-0137903955. (anglicky)
  29. BERKA, Petr. Dobývání znalostí z databází. Praha: Academia, 2003. ISBN 80-200-1062-9.
  30. MOON, Todd K.; STIRLING, Wynn C. Mathematical Methods and Algorithms for Signal Processing. Upper Saddle River, NJ: Prentice Hall, 1999. ISBN 978-0201361865. (anglicky)
  31. ASTROM, Karl J. Introduction to Stochastic Control Theory. Mineola, NY: Dover Publications, 2006. ISBN 978-0486445311. (anglicky)
  32. MONTGOMERY, Douglas C. Introduction to Statistical Quality Control. [s.l.]: Wiley, 2008. ISBN 978-0470169926. (anglicky)
  33. SMITH, David J. Reliability, Maintainability and Risk, Seventh Edition: Practical Methods for Engineers including Reliability Centred Maintenance and Safety-Related Systems. Oxford: Butterworth-Heinemann, 2005. ISBN 978-0750666947. (anglicky)
  34. ZÍTEK, František. Ztracený čas: Elementy teorie hromadné obsluhy. Praha: Academia, 1969.
  35. BERKA, Petr. Dobývání znalostí z databází. Praha: Academia, 2003. ISBN 80-200-1062-9., s. 271–290

Externí odkazy

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.