Lineární funkce

Každá funkce ${\displaystyle f}$ je lineární, na množině ${\displaystyle R(D_{f}=R)}$, a je dána předpisem: ${\displaystyle f:y=ax+b,}$ kde ${\displaystyle a}$ i ${\displaystyle b}$ jsou konstanty.

Lineární funkce
Lineární funkce 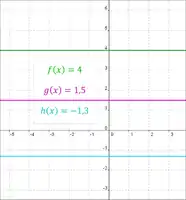${\displaystyle y=ax+b}$	Lineární funkce konstantní ${\displaystyle y=b}$	Přímá úměrnost ${\displaystyle y=ax}$
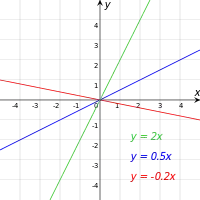
Grafem je přímka procházející bodem ${\displaystyle \left[0;b\right]}$ Je rostoucí (klesající) v celém ${\displaystyle D_{f}}$a tedy prostá. Není shora ani zdola omezená. Nemá maximum ani minimum.	Grafem je přímka rovnoběžná s osou ${\displaystyle x}$ a procházející bodem${\displaystyle \left[0;b\right]}$ Není rostoucí ani klesající, je omezená. Pro každé ${\displaystyle x\in D_{f}}$ má maximum i minimum.	Grafem je přímka procházející bodem 0${\displaystyle \left[0;0\right]}$ Je rostoucí (klesající) v celém ${\displaystyle D_{f}}$a tedy prostá. Není shora ani zdola omezená. Je lichá funkce. Nemá maximum ani minimum.[1]

• lineární funkce je uzavřená na skládání
• lineární funkce není ohraničená ani periodická
• pro ${\displaystyle a>0}$ je lineární funkce rostoucí, pro ${\displaystyle a<0}$ je klesající
• lineární funkce je spojitá
• lineární funkce má v každém bodě derivaci, která je rovna její směrnici
• primitivní funkce k lineární funkci je kvadratická funkce
  • příklad: ${\displaystyle \int (3x+2)\,dx={3 \over 2}x^{2}+2x+C}$

Lineární funkce s absolutními hodnotami jsou takové lineární funkce, které mají v předpisu funkce jednu nebo více absolutních hodnot, ve kterých jsou výrazy s proměnnou.

Pro nezáporné argumenty je tato funkce totožná s funkcí${\displaystyle f:y=x;}$ pro ${\displaystyle x\geq 0}$, pro záporné argumenty je tato funkce totožná s funkcí ${\displaystyle f:y=-x;}$ pro ${\displaystyle x\leq 0}$. Zápis funkce ${\displaystyle f:y=|x|}$[2]

Vlastnosti

Funkce s absolutní hodnotou

Je dána funkce ${\displaystyle f:y=|x|}$; obor hodnot ${\displaystyle H_{f}=\langle 0,\infty {\bigr )}}$ a definiční obor funkce ${\displaystyle D_{f}=R}$

Funkce absolutní hodnota není na svém definičním oboru ani rostoucí, ani klesající. Na intervalu ${\displaystyle (-\infty ,0)}$  je tato funkce klesající a na intervalu ${\displaystyle \langle 0,\infty {\bigr )}}$ je rostoucí.

Grafem funkce jsou dvě polopřímky, které mají společný počátek v bodě 0 ${\displaystyle [0,0]}$ Funkce absolutní hodnota je sudá, není prostá, není periodická a je omezená zdola.[2]

• Lineární rovnice
• Konstantní funkce
• Parita funkce
• Přímka
• Lineární lomená funkce
• Lineární kombinace
• Lineární zobrazení

• Obrázky, zvuky či videa k tématu lineární funkce na Wikimedia Commons