600nadstěn
V geometrii je šestisetnadstěn (což je volný překlad anglického 600-cell), nebo také hexakosichoron platónské těleso ve čtyřrozměrném prostoru. Bývá považován za čtyřrozměrnou analogii dvacetistěnu.
| 600nadstěn | |
|---|---|
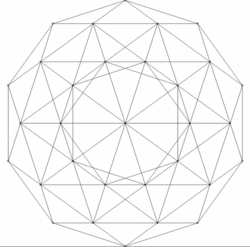 | |
| Typ | Pravidelný polychoron |
| Nadstěn | 600 (3.3.3) |
| Stěn | 1200 {3} |
| Hran | 720 |
| Vrcholů | 120 |
| Uspořádání vrcholů | 20 (3.3.3) (dvacetistěn) |
| Schläfliho symbol | {3,3,5} |
| Grupa symetrie | grupa [3,3,5] |
| Duální těleso | 120nadstěn |
| Vlastnosti | konvexní |
3povrch 600nadstěnu je tvořen ze 600 nadstěn majících tvar čtyřstěnu. V jednom vrcholu se potkává 20 nadstěn. 600nadstěn má 1 200 trojúhelníkových stěn, 720 hran a 120 vrcholů. Duálním tělesem je 120nadstěn.
Objem, povrch a další parametry
Následující vzorce udávají, jaký je objem 600nadstěnu, a jeho k-rozměrné povrchy (což je vždy obsah k-rozměrné stěny krát počet těchto stěn) v závislosti na hraně a.[1]
je tedy délka všech hran kostry 600nadstěnu.
Poloměr vepsané koule je
a poloměr koule opsané je
Kartézská soustava souřadnic
Je-li délka hrany 1/φ (kde φ = (1+√5)/2 je zlatý řez), pak 120 vrcholů 600nadstěnu má následující souřadnice:
- (±½,±½,±½,±½), (všechny kombinace znamének ⇒ 16 vrcholů)
- (0,0,0,±1) (permutace přes všechny souřadnice ⇒ 8 vrcholů)
- ½(±1,±φ,±1/φ,0) (sudé permutace ⇒ 96 vrcholů).
Přitom zjevně prvních 16 vrcholů jsou vrcholy teseraktu, následujících 8 vrcholů tvoří vrcholy 16nadstěnu prvních 16+8 vrcholů tvoří dohromady vrcholy 24nadstěnu.
Pokud tyto čtveřice souřadnic interpretujeme jako kvaterniony, potom 120 vrcholů 600nadstěnu tvoří uzavřenou konečnou grupu, která je izomorfní grupě SL(2,5).
| Vícerozměrná geometrická tělesa | ||||
|---|---|---|---|---|
| d=2 | trojúhelník | čtverec | šestiúhelník | pětiúhelník |
| d=3 | tetraedr | krychle, oktaedr | krychloktaedr, kosočtverečný dvanáctistěn | dvanáctistěn, dvacetistěn |
| d=4 | 5nadstěn | teserakt, 16nadstěn | 24nadstěn | 120nadstěn, 600nadstěn |
| d=5 | 5simplex | penterakt, 5ortoplex | ||
| d=6 | 6simplex | hexerakt, 6ortoplex | ||
| d=7 | 7simplex | hepterakt, 7ortoplex | ||
| d=8 | 8simplex | okterakt, 8ortoplex | ||
| d=9 | 9simplex | ennerakt, 9ortoplex | ||
| d=10 | 10simplex | dekerakt, 10ortoplex | ||
| d=11 | 11simplex | hendekerakt, 11ortoplex | ||
| d=12 | 12simplex | dodekerakt, 12ortoplex | ||
| d=13 | 13simplex | triskaidekerakt, 13ortoplex | ||
| d=14 | 14simplex | tetradekerakt, 14ortoplex | ||
| d=15 | 15simplex | pentadekerakt, 15ortoplex | ||
| d=16 | 16simplex | hexadekerakt, 16ortoplex | ||
| d=17 | 17simplex | heptadekerakt, 17ortoplex | ||
| d=18 | 18simplex | oktadekerakt, 18ortoplex | ||
| d=19 | 19simplex | ennedekerakt, 19ortoplex | ||
| d=20 | 20simplex | ikosarakt, 20ortoplex | ||
Externí odkazy
 Obrázky, zvuky či videa k tématu 600nadstěn na Wikimedia Commons
Obrázky, zvuky či videa k tématu 600nadstěn na Wikimedia Commons
- HyperSolids je open source program pro Macintosh (Mac OS X a vyšší).
Reference
- FONTAINE, David A. [cit. 2010-08-01]. Dostupné v archivu pořízeném dne 02-07-2004. (anglicky)