Tvar Zeme

Pohľad cez záliv široký 20 km na pobreží Španielska . Všimnite si zakrivenie Zeme zakrývajúce základňu budov na vzdialenom pobreží.

Najjednoduchším modelom pre tvar celej Zeme je guľa. Polomer Zeme je vzdialenosť od stredu Zeme k jej povrchu, asi 6 371 km. Zatiaľ čo „polomer“ je zvyčajne charakteristický pre dokonalé gule, Zem sa od sférického tvaru odchýli len o tretinu percenta, dostatočne blízko na to, aby sa s ním v mnohých kontextoch zaobchádzalo ako s guľou a aby sa ospravedlňoval termín „polomer Zeme“.

Koncept sférickej Zeme sa datuje okolo 6. storočia pred n.l.,[2] ale do 3. storočia pred n.l. zostal záležitosťou filozofických špekulácií. Prvý vedecký odhad polomeru Zeme dal Eratosthenes asi 240 pred n.l., s odhadmi presnosti merania Eratosthenesa v rozsahu od 2% do 15%.

Zem je iba približne sférická, takže ako jej prirodzený polomer neslúži žiadna jedná hodnota. Vzdialenosti bodov na povrchu k stredu sa pohybujú od 6 353 do 6 384 km. Niekoľko rôznych spôsobov modelovania Zeme ako gule poskytujú priemerný polomer 6 371 km. Bez ohľadu na model, akýkoľvek polomer spadá medzi polárne minimum okolo 6 357 km a rovníkové maximum asi 6 378 km. Rozdiel 21 km zodpovedá rozdielu polomeru rovníka a polárneho polomeru. Polárny polomer je približne o 0,3% kratší ako polomer rovníka.

Sploštený sféroid, vysoko zväčšené sploštenie v porovnaní so skutočnou Zemou

Mierka spološtenia z roku 2003 IERS referenčný elipsoid. Vonkajší okraj tmavo modrej čiary je elipsa s rovnakou excentricitou ako Zem. Na porovnanie, svetlo modrý kruh vo vnútri má priemer rovnajúci sa vedľajšia osi elipsy. Červená krivka predstavuje Kármánovu hranicu 100 km nad hladinou mora, zatiaľ čo žltý pás označuje výškový rozsah ISS na nízkej obežnej dráhe Zeme .

Pretože Zem je sploštená na póloch a vydutá na rovníku, predstavuje geodézia tvar Zeme ako sploštený sféroid. Sploštený sféroid alebo sploštený elipsoid je rotačný elipsoid získaný rotáciou elipsy okolo jej kratšej osi. Je to pravidelný geometrický tvar, ktorý takmer zodpovedá tvaru Zeme. Sféroid popisujúci tvar Zeme alebo iného nebeského tela sa nazýva referenčný elipsoid. Referenčný elipsoid pre Zem sa nazýva elipsoid Zeme .

Rotačný elipsoid je jednoznačne definovaný dvoma parametrami. V geodézii sa používa niekoľko konvencií na vyjadrenie týchto dvoch veličín, všetky sú však navzájom rovnocenné a navzájom sa môžu prevádzať:

• Rovníkový polomer ${\displaystyle a}$ (hlavná os) a polárny polomer ${\displaystyle b}$ (vedľajšia os);
• ${\displaystyle a}$ a excentricita ${\displaystyle e}$ ;
• ${\displaystyle a}$ a sploštenie ${\displaystyle f}$ ,

Excentricita a sploštenie sú rôzne spôsoby vyjadrenia toho, ako je stlačený elipsoid. Ak sa sploštenie objaví v geodézii ako jedna z definujúcich veličín, vo všeobecnosti sa vyjadruje jeho recipročnou hodnotou. Napríklad v sféroide WGS 84 ktorý používajú dnešné systémy GPS, recipročné sploštenie ${\displaystyle 1/f}$ je presne 298,257223 563.

Rozdiel medzi guľou a referenčným elipsoidom pre Zem je malé, iba asi jedna časť z 300. Historicky bolo sploštenie vypočítané z meraní stupňov. V súčasnosti sa používajú geodetické siete a satelitná geodézia. V praxi sa v priebehu storočí vyvinulo mnoho referenčných elipsoidov z rôznych prieskumov. Hodnota sploštenia sa mierne líši od jedného referenčného elipsoidu k druhému, odrážajúc miestne podmienky a to, či je referenčný elipsoid určený na modelovanie celej Zeme alebo len jej časti.

Guľa má jediný polomer zakrivenia, čo je jednoducho polomer gule. Zložitejšie povrchy majú polomery zakrivenia, ktoré sa líšia po povrchu. Polomer zakrivenia opisuje polomer gule, ktorý najlepšie aproximuje povrch v tomto bode. Sploštené elipsoidy majú konštantný polomer zakrivenia východne - západne pozdĺž rovnobežiek, ak je na povrchu nakreslená mriežka, ale zakrivenie sa mení iným smerom. Pre sploštený elipsoid, polárny polomer zakrivenia ${\displaystyle r_{p}}$ je väčší ako rovník

${\displaystyle r_{p}={\frac {a^{2}}{b}},}$

pretože pól je sploštený: čím je plocha plochšia, tým musí byť guľa väčšia, aby sa jej priblížila. Naopak, polomer zakrivenia elipsoidu na severe a juhu je pri rovníku ${\displaystyle r_{e}}$ je menšia ako polárny

${\displaystyle r_{e}={\frac {b^{2}}{a}}}$

kde ${\displaystyle a}$ je vzdialenosť od stredu elipsoidu k rovníku (hlavná polosa) a ${\displaystyle b}$ je vzdialenosť od stredu k pólu. (vedľajšia polosa)

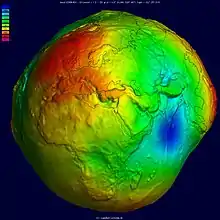
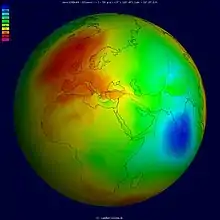
Merania sa vykonávajú na zdanlivom alebo topografickom povrchu Zeme a výpočty sa vykonávajú na elipsoide. Iný povrch sa používa na geodetické merania: geoid . Pri geodetickom prieskume sa výpočet geodetických súradníc bodov obyčajne vykonáva na referenčnom elipsoide, ktorý sa v oblasti prieskumu približuje veľkosti a tvaru Zeme. Skutočné merania vykonané na povrchu Zeme pomocou určitých nástrojov sa však vzťahujú na geoid. Elipsoid je matematicky definovaná pravidelná plocha so špecifickými rozmermi. Geoid sa naopak zhoduje s tým povrchom, ku ktorému by sa oceány prispôsobili po celej Zemi, ak by sa mohli prispôsobiť kombinovanému účinku hmotnej príťažlivosti Zeme (gravitácii) a odstredivej sile zemskej rotácie . V dôsledku nerovnomerného rozloženia zemskej hmoty je geoidný povrch nepravidelný a keďže elipsoid je pravidelný povrch, rozdiely medzi nimi, označované ako geoidné zvlnenia, geoidálne výšky alebo geoidné separácie, budú nepravidelné rozložené.

Geoid je povrch, po ktorom je gravitačný potenciál všade rovnaký a na ktorý je smer gravitácie vždy kolmý (pozri ekvipotenciálny povrch). Kolmosť je zvlášť dôležitá, pretože optické prístroje obsahujúce gravitačné referenčné nivelačné zariadenia sa bežne používajú na vykonávanie geodetických meraní. Pri správnom nastavení sa zvislá os nástroja zhoduje so smerom gravitácie, a preto je kolmá na geoid. Uhol medzi ohybovou čiarou, ktorý je kolmý na geoid (niekedy nazývaný „vertikál“) a kolmý na elipsoid (niekedy nazývaný „elipsoidná normál“), je definovaný ako vychýlenie vertikály . Má dve zložky: východ-západ a sever-juh.

Geoidné zvlnenie vo falošnej farbe, tieňované reliéfy, zvislá mierka je zväčšená 10 000 krát.

Geoidné zvlnenie vo falošnej farbe v mierke.

Možnosť, že rovník Zeme je lepšie charakterizovaný skôr ako elipsa ako kruh, a preto je elipsa tri axiálna, je vecou vedeckého bádania už mnoho rokov.[3][4] Moderný technologický vývoj poskytol nové a rýchle metódy zberu údajov a od uvedenia Sputniku 1 sa orbitálne údaje použili na skúmanie teórie elipticity. Najnovšie výsledky naznačujú 70 m rozdiel medzi dvoma rovníkovými hlavnými a vedľajšími osami zotrvačnosti, s väčšou polosou smerujúcou k 15° západnej zemepisnej dĺžky. [5] [6]

Druhá teória, zložitejšia ako tri osi navrhla, že pozorované dlhé periodické orbitálne variácie prvých pozemských satelitov naznačujú ďalšiu depresiu na južnom póle sprevádzanú vydutím rovnakého stupňa na severnom póle. Tvrdí sa tiež, že severné stredné šírky boli mierne sploštené a južné stredné šírky boli vypuklé v podobnom množstve. Táto koncepcia navrhla mierne hruškovitú Zem a bola predmetom mnohých verejných diskusií po vypustení prvých umelých satelitov.

Moderná geodézia má tendenciu udržať rotačný elipsoid ako referenčný elipsoid a zaobchádza s tri axialitou a tvarom hrušky ako s časťou geoidného útvaru: sú reprezentované sférickými harmonickými koeficientmi ${\displaystyle C_{22},S_{22}}$ a ${\displaystyle C_{30}}$ zodpovedajúc stupňom 2,2 pre tri ososť a pre hruškovitý tvar 3,0.

Sú možné jednoduchšie lokálne aproximácie, napr. Oscilačná guľa a lokálna tangenciálna rovina.