Elipsa

Elipsa je rovinná krivka, ktorá patrí do triedy kužeľosečiek. Elipsu možno definovať aj takto: je to množina všetkých bodov roviny, ktoré majú od dvoch pevných bodov F1 a F2 konštantný súčet vzdialeností, ktorý je väčší ako vzdialenosť týchto bodov. Body F1, F2 sa nazývajú ohniská, priamka prechádzajúca bodmi F1, F2 sa nazýva hlavná os elipsy, body A, B v ktorých os elipsy pretína elipsu sú hlavné vrcholy elipsy, stred úsečky F1, F2 je stred elipsy a priamka kolmá na hlavnú os elipsy prechádzajúca jej stredom je vedľajšia os elipsy a body C, D, v ktorých vedľajšia os elipsy pretína elipsu sú vedľajšie vrcholy elipsy.

O literárnom termíne pozri elipsa (literatúra).

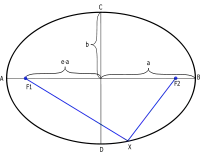
Ak zvolíme súradnicovú os tak, aby jej začiatok bol stred elipsy, x-ová os bola hlavná os elipsy a y-ová os bola vedľajšia os súradnice bodov budú:

F1=(-f,0), F2=(f,0), A=(-a,0), B=(a,0), C=(0,b), D=(0,-b)

Všeobecná rovnica elipsy je:

${\displaystyle Ax^{2}+By^{2}+Cx+Dy+E=0}$

Stredová rovnica elipsy je:

${\displaystyle \left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=1}$

Parametrické rovnice elipsy sú:

${\displaystyle x=a.\cos(\varphi )}$

${\displaystyle y=b.\sin(\varphi )}$

Užitočné vzťahy:

${\displaystyle f^{2}=a^{2}-b^{2}}$

${\displaystyle e=f/a}$

Plocha elipsy:

${\displaystyle A=\pi \cdot a\cdot b}$

Symboly v rovniciach:

a je hlavná polos

b je vedľajšia polos

e je excentricita elipsy

f je ohnisková vzdialenosť; vzdialenosť medzi ohniskom a stredom elipsy.

φ je uhol 0 ≤ φ < 2π ako parameter

A, B, C, D, E sú koeficienty, pričom platí A > 0, B > 0 a A ≠ B

A je vo vzorci plochy plochou

Elipsa má veľký význam pri aplikácii matematiky vo fyzike, astronómii a v technike. Napríklad dráhy planét sú elipsy, v teórii pružnosti sa pracuje s elipsou inercie a elipsou napätia,...

Elipsu možno definovať aj ako kužeľosečku, je to prienik roviny s kužeľovou plochou, pričom rovina nie je kolmá na os kužeľovej plochy a zviera s osou väčší uhol, ako priamka, ktorej rotáciou kužeľová plocha vznikla.

Špeciálnym prípadom elipsy je kružnica. Je to elipsa, kde F1=F2 a súčasne polomer kružnice R = a = b.

Ak v elipse umiestnime svetelný zdroj do jedného ohniska, všetky lúče sa odrazia do druhého ohniska.