Rovníkové vydutie
Rovníkové vydutie alebo rovníková výduť[1] je rozdiel medzi rovníkovým a polárnym priemerom planéty v dôsledku odstredivej sily vytváranej rotáciou okolo osi telesa. Rotujúce teleso má tendenciu pretvárať guľu na sploštený sféroid.
Na Zemi
Zem má pomerne malé rovníkové vydutie: rovník je okolo 43 km širší ako priemer cez póly, čo je rozdiel blízky 1/300 priemeru. Keby sa Zem zmenšila na zemeguľu s priemerom 1 meter na rovníku, tento rozdiel by bol iba 3 milimetre. Aj keď je tento rozdiel príliš malý na to, aby sa dal vizuálne všimnúť, tento rozdiel je stále viac ako dvakrát najväčšia odchýlka skutočného povrchu od elipsoidu vrátane najvyšších hôr a najhlbších oceánskych priekop.
Rotácia Zeme ovplyvňuje aj hladinu mora, pomyselnú plochu, z ktorej sa meria nadmorská výška. Tento povrch sa zhoduje so strednou hladinou vody v oceánoch a extrapoluje sa po súši, pričom sa berie do úvahy miestny gravitačný potenciál a odstredivá sila.
Rozdiel polomerov je teda asi 21 km. Pozorovateľ, ktorý stojí na hladine mora na oboch póloch, je preto 21 km bližšie k stredu Zeme, než keby stál na hladine mora na rovníku. Výsledkom je, že najvyšší bod na Zemi meraný od stredu k povrchu je skôr vrchol hory Chimborazo v Ekvádore než Mount Everest. Keďže však oceán sa odstredivou silou vyduje, podobne ako Zem a aj jeho atmosféra, nie je Chimborazo tak vysoko nad morom ako Everest.
Presnejšie povedané, povrch Zeme sa zvyčajne aproximuje ideálnym splošteným elipsoidom na účely presného definovania zemepisnej šírky a dĺžky pre kartografiu, ako aj „stredu Zeme“. V štandardnom zemskom elipsoide WGS-84, ktorý sa bežne používa pri tvorbe máp a systéme GPS, sa predpokladá, že polomer Zeme je 6 378,137 km na rovníku a polárny je 6 356,7523142 km; čo znamená rozdiel 21,3846858 km v polomeroch, 42,7693716 km v priemeroch a relatívnym sploštením 1/298,257223563. Hladina hladiny mora je oveľa bližšie k tomuto štandardnému elipsoidu, ako je povrch pevnej Zeme.
Rovnováha ako rovnováha energií
Gravitácia má tendenciu sťahovať nebeské teleso do gule, ktorej tvar má všetku hmotu čo najbližšie k ťažisku. Rotácia spôsobuje zdeformovanie z tohto guľového tvaru; spoločnou mierou skreslenia je sploštenie (niekedy nazývané elipticita alebo oblatita), ktoré môže závisieť od množstva faktorov vrátane veľkosti, uhlovej rýchlosti, hustoty a elasticity.
Aby ste získali cit pre daný druh rovnováhy, predstavte si niekoho, kto sedí v rotujúcej otočnej stoličke so závažiami v rukách. Ak osoba v kresle pritiahne závažia smerom k sebe, robí prácu a zvyšuje sa rotačná kinetická energia. Zvýšenie rýchlosti otáčania je také silné, že pri vyššej rýchlosti otáčania je požadovaná dostredivá sila väčšia ako pri počiatočnej rýchlosti otáčania.
Pri formovaní planéty sa niečo podobné deje. Hmota sa najprv zhlukuje do pomaly rotujúceho diskovitého rozdelenia a kolízie, trenie prevádzajú kinetickú energiu na teplo, čo umožňuje disku gravitačne vytvárať veľmi sploštený sféroid.
Pokiaľ je protoplanéta stále príliš vyrovnaná na to, aby bola v rovnováhe, uvoľňovanie energie gravitačného potenciálu pri kontrakcii stále vedie k nárastu rotačnej kinetickej energie. Ako kontrakcia pokračuje, rýchlosť rotácie neustále stúpa, a preto sila potrebná na ďalšie kontrakciu neustále stúpa. Je miesto, kde by nárast rotačnej kinetickej energie pri ďalšej kontrakcii bol väčší ako uvoľnená energia gravitačného potenciálu. Proces sťahovania môže pokračovať až do tohto bodu, v ktorom sa zastaví.
Pokiaľ neexistuje rovnováha, môže dôjsť k násilnej konvekcií a pokiaľ dôjde k násilnej konvekcií, môže trenie konvertovať kinetickú energiu na teplo, čím sa zo systému vypustí rotačná kinetická energia. Po dosiahnutí rovnovážneho stavu prestane konverzia kinetickej energie na teplo. V tomto zmysle je rovnovážny stav najnižší stav energie, ktorý sa dá dosiahnuť.
Miera rotácie Zeme sa stále spomaľuje, aj keď postupne, asi o dve tisíciny sekundy na rotáciu každých 100 rokov. Odhady rýchlosti rotácie Zeme sa v minulosti líšili, pretože nie je presne známe, ako sa vytvoril Mesiac. Odhady zemskej rýchlosti rotácie pred 500 miliónmi rokov sa pohybujú okolo 20 hodín za „deň“.
Rýchlosť rotácie Zeme sa spomaľuje hlavne kvôli slapovým interakciám s Mesiacom a Slnkom. Pretože tuhé časti Zeme sú rozťažné, so znižovaním rýchlosti rotácie rovníkové vydutie Zeme postupne klesalo.
Rozdiely v gravitačnom zrýchlení
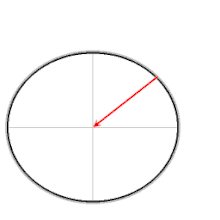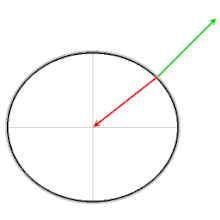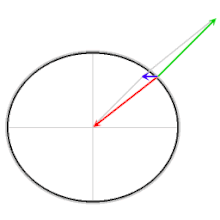
Červená šípka: gravitácia
Zelená šípka, normálova sila
Modrá šípka: výsledná sila
Výsledná sila poskytuje požadovanú strednú silu. Bez tejto dostredivej sily by sa objekty bez trenia posúvali smerom k rovníku. Pri výpočtoch, keď sa použije súradnicový systém, ktorý sa otáča spolu so Zemou, ukazuje vektor pomyselnej odstredivej sily smerom von a je rovnako veľký ako vektor predstavujúci stredovú silu
Vďaka rotácii planéty okolo svojej vlastnej osi je gravitačné zrýchlenie na rovníku menšie ako na póloch. V 17. storočí francúzski vedci po vynáleze kyvadlových hodín zistili, že hodiny poslané do Francúzskej Guyany na severnom pobreží Južnej Ameriky bežali pomalšie ako ich presné náprotivky v Paríži. Pri meraní zrýchlenia v dôsledku gravitácie na rovníku sa musí zohľadniť aj rotácia planéty. Akýkoľvek objekt, ktorý je vzhľadom na povrch Zeme stacionárny, v skutočnosti sleduje kruhovú trajektóriu obiehajúcu okolo zemskej osi. Vytiahnutie objektu do takejto kruhovej dráhy vyžaduje silu. Odstredivé zrýchlenie pozdĺž rovníka pri jednej otáčke za hviezdny deň, je 0,0339 m/s2. Toto zrýchlenia znižuje efektívne gravitačné zrýchlenie. Na rovníku je zrýchlenie 9,7805 m/s2. To znamená, že skutočné gravitačné zrýchlenie na rovníku musí byť 9,8144 m/s2 (9,7805+0,0339 =9,8144).
Na póloch je gravitačné zrýchlenie 9,8322 m/s2. Rozdiel 0,0187 m/s2 medzi gravitačným zrýchlením na póloch a skutočným gravitačným zrýchlením na rovníku je to, že objekty umiestnené na rovníku sú asi 21 kilometrov ďalej od ťažiska zeme ako na póloch, čo zodpovedá menšiemu počtu gravitačné zrýchlenie.
Stručne povedané, existujú dva príspevky k tomu, že efektívne gravitačné zrýchlenie je na rovníku menej silné ako na póloch. Okolo 70 percent rozdielu je spôsobené skutočnosťou, že objekty obiehajú okolo zemskej osi a asi 30 percent je spôsobené sférickým tvarom Zeme.
Diagram ukazuje, že vo všetkých zemepisných šírkach je efektívne gravitačné zrýchlenie znížené požiadavkou na poskytnutie centripetálnej sily; znižujúci účinok je najsilnejší na rovníku.
Vplyv na satelitné dráhy
Skutočnosť, že gravitačné pole Zeme sa mierne odchyľuje od sféricky symetrického, ovplyvňuje aj obežné dráhy satelitov prostredníctvom sekulárnych orbitálnych precesií.[2][3][4] Závisia od orientácie zemskej symetrickej osi v inerciálnom priestore a vo všeobecnosti ovplyvňujú všetky keplerovské orbitálne prvky s výnimkou veľkej osi. V prípade, že referenčná z os súradnicového systému je zarovnaná pozdĺž zemskej osi symetrie, potom iba dĺžka výstupného uzla Ω, argument šírky pericentera ω a stredná anomália M podrobujú sa sekulárnej precessii.[5]
Takéto poruchy, ktoré sa predtým používali na mapovanie zemského gravitačného poľa z vesmíru[6] môžu hrať významnú rušivú úlohu, keď sa satelity používajú na testovanie všeobecnej relativity[7] pretože oveľa menšie relativistické účinky sú kvalitatívne nerozoznateľné od oblatity - poruchy spôsobené rotáciou.
Ostatné nebeské telesá
Všeobecne akékoľvek nebeské teleso, ktoré sa otáča (a ktoré je dostatočne masívne na to, aby sa vtiahlo do sférického alebo takmer sférického tvaru), bude mať rovníkové vydutie zodpovedajúcu jeho rýchlosti rotácie. Saturn je planéta s najväčším rovníkovým vydutím v Slnečnej sústave (11 808 km).
Nasleduje tabuľka rovníkového vydutia niektorých veľkých nebeských telies Slnečnej sústavy:
| Teleso | Rovníkový priemer | Polárny priemer | Rovníkové vydutie | Pomer sploštenia |
|---|---|---|---|---|
| Zem | 12 756,27 km | 12 713,56 km | 42,77 km | 1: 298,2575 |
| Mars | 6 805 km | 6 754,8 km | 50,2 km | 1: 135,56 |
| Ceres | 975 km | 909 km | 66 km | 1: 14,77 |
| Jupiter | 143 884 km | 133 709 km | 10 175 km | 1: 14,14 |
| Saturn | 120 536 km | 108 728 km | 11 808 km | 1: 10,21 |
| Urán | 51 118 km | 49 946 km | 1 172 km | 1: 43,62 |
| Neptún | 49 528 km | 48 682 km | 846 km | 1: 58,54 |
Rovníkové vydutie by sa nemalo zamieňať s rovníkovými hrebeňmi. Rovníkové hrebene sú najmenej u troch Saturnových mesiacov: veľký mesiac Japetus a malé mesiace Atlas, Pan a Daphnis. Tieto hrebene pozorne sledujú rovníky mesiacov. Hrebene sa zdajú byť jedinečné pre saturnský systém, nie je však jasné, či sú tieto udalosti súvisiace alebo náhoda. Prvé tri boli objavené sondou Cassini v roku 2005; hrebeň u Dafné bol objavený v roku 2017. Hrebeň na Japetuse je takmer 20 km široký, 13 km vysoký a 1 300 km dlhý. Hrebeň na Atlase je ešte úmerne výraznejší vzhľadom na oveľa menšiu veľkosť mesiaca, čo mu dodáva tvar disku. Obrázky Pan ukazujú štruktúru podobnú Atlasu, zatiaľ čo štruktúra na Daphnis je menej výrazná.
Formulácia
Koeficient sploštenia pre rovnovážnu konfiguráciu gravitačného sféroidu, zloženého z nestlačiteľnej tekutiny s rovnomernou hustotou, rotujúcej stabilne okolo pevnej osi, pre malú mieru sploštenia, sa aproximuje:[8]
kde:
- a sú rovníkový a polárny polomer,
- je stredný polomer,
- je uhlová rýchlosť,
- je doba rotácie,
- je univerzálna gravitačná konštanta,
- je celková telesná hmotnosť
- je hustota telesa
Referencie
- Súradnice na oblohe - Miroslav Znášik, Hvezdáreň v Žiline, Horný Val 20/41, 010 01 Žilina [online]. [Cit. 2019-12-27]. Dostupné online.
- IORIO, L.. Perturbed stellar motions around the rotating black hole in Sgr ${\mathrm{A}}^{*}$ for a generic orientation of its spin axis. Physical Review D, 2011-12-01, roč. 84, čís. 12, s. 124001. Dostupné online [cit. 2019-12-26]. DOI: 10.1103/PhysRevD.84.124001.
- RENZETTI, G.. Satellite Orbital Precessions Caused by the Octupolar Mass Moment of a Non-Spherical Body Arbitrarily Oriented in Space. Journal of Astrophysics and Astronomy, 2013-12-01, roč. 34, čís. 4, s. 341–348. Dostupné online [cit. 2019-12-26]. ISSN 0973-7758. DOI: 10.1007/s12036-013-9186-4. (po anglicky)
- RENZETTI, G.. Satellite orbital precessions caused by the first odd zonal J3 multipole of a non-spherical body arbitrarily oriented in space. Astrophysics and Space Science, 2014-08-01, roč. 352, čís. 2, s. 493–496. Dostupné online [cit. 2019-12-26]. ISSN 1572-946X. DOI: 10.1007/s10509-014-1915-x. (po anglicky)
- KING-HELE, D. G.. The Earth's Gravitational Potential, deduced from the Orbits of Artificial Satellites. Geophysical Journal International, 1961-12-01, roč. 4, čís. Supplement_1, s. 3–16. Dostupné online [cit. 2019-12-26]. ISSN 0956-540X. DOI: 10.1111/j.1365-246X.1961.tb06801.x. (po anglicky)
- KING-HELE, D. G.. Geophysical researches with the orbits of the first satellites. Geophysical Journal International, 1983-07-01, roč. 74, čís. 1, s. 7–23. Dostupné online [cit. 2019-12-26]. ISSN 0956-540X. DOI: 10.1111/j.1365-246X.1983.tb01868.x. (po anglicky)
- RENZETTI, G.. Are higher degree even zonals really harmful for the LARES/LAGEOS frame-dragging experiment?. Canadian Journal of Physics, 2012-08-03, roč. 90, čís. 9, s. 883–888. Dostupné online [cit. 2019-12-26]. ISSN 0008-4204. DOI: 10.1139/p2012-081.
- Rotational Flattening [online]. farside.ph.utexas.edu, [cit. 2019-12-26]. Dostupné online.