Trojuholník

Trojuholník je jeden zo základných rovinných geometrických útvarov; mnohouholník s troma vrcholmi a stranami. Je to dvojrozmerný útvar, ktorého súčet vnútorných uhlov je vždy 180°.

O iných významoch výrazu Trojuholník pozri Trojuholník (rozlišovacia stránka).

Definícia trojuholníka

Trojuholník môžeme definovať ako prienik troch polrovín.
Ak máme tri rôzne body A, B, C, (ktoré neležia na jednej priamke) tak trojuholníkom s vrcholmi A, B, C nazývame prienik polrovín ABC, ACB, BCA.
Úsečky AB, BC, CA sú stranami tohto trojuholníka a ich zjednotenie je obvod trojuholníka.

Pre strany trojuholníka musí platiť trojuholníková nerovnosť, t. j., že súčet dĺžok dvoch ľubovoľných strán je väčší ako dĺžka tretej strany, teda:

$a+b>c$
$b+c>a$
$a+c>b$

Klasifikácia trojuholníkov

Trojuholníky možno triediť podľa viacerých kritérií:

Podľa dĺžky jeho strán

Rovnostranný trojuholník – všetky strany majú rovnakú dĺžku. Rovnostranný trojuholník je tiež rovnouhlý, t. j. všetky jeho vnútorné uhly majú rovnakú veľkosť, a to 60°; je to pravidelný mnohoulník.[1]
Rovnoramenný trojuholník – má práve dve strany rovnakej dĺžky. Rovnoramenný trojuholník má tiež dva rovnaké vnútorné uhly (sú to uhly, v ktorých obe rovnaké strany sa napájajú na tretiu-základňu).
Rovnostranný trojuholník je tiež rovnoramenným, ale nie každý rovnoramenný trojuholník je rovnostranný.[2]
Rôznostranný trojuholník – všetky strany majú rozličnú dĺžku. Jeho vnútorné uhly sú taktiež rozdielne.[3]


Rovnostranný	Rovnoramenný	Rôznostranný

Podľa veľkosti najväčšieho vnútorného uhla:

Pravouhlý trojuholník – má práve jeden vnútorný uhol s veľkosťou 90° (pravý uhol). Strana ležiaca oproti pravému uhlu sa nazýva prepona a je najdlhšou stranou v trojuholníku. Ostatné dve strany sa nazývajú odvesny.
Tupouhlý trojuholník – má práve jeden vnútorný uhol väčší ako 90° (tupý uhol) a ostatné uhly má ostré.
Ostrouhlý trojuholník – má všetky vnútorné uhly menšie ako 90° (tri ostré uhly).


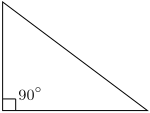Pravouhlý	Tupouhlý	Ostrouhlý

Vlastnosti

Výška trojuholníka

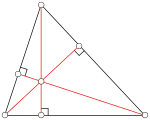
Výšky a ortocentrum ostrouhlého trojuholníka.

Je to úsečka na priamke prechádzajúcej vrcholom trojuholníka a je kolmá na protiľahlú stranu. V ľubovoľnom trojuholníku prechádzajú všetky tri výšky jedným bodom, ktorý nazývame ortocentrum. Ortocentrum má polohu:

vnútri trojuholníka – ak je trojuholník ostrouhlý,
na vrchole pravého uhla – ak je trojuholník pravouhlý,
mimo trojuholníka – ak je trojuholník tupouhlý.

Výpočet výšky trojuholníka:

v_{a}=c\cdot \sin \beta =b\cdot \sin \gamma

v_{b}=a\cdot \sin \gamma =c\cdot \sin \alpha

v_{c}=b\cdot \sin \alpha =a\cdot \sin \beta

Ťažnice trojuholníka

Ťažnice trojuholníka a ťažisko.

Ťažnice sú úsečky, ktoré spájajú vrcholy trojuholníka so stredmi protiľahlých strán. Prechádzajú jedným bodom, ktorý voláme ťažisko. Ťažisko delí každú z ťažníc v pomere 2 : 1, pričom dlhšia časť je medzi vrcholom a ťažiskom, a kratšia časť medzi ťažiskom a stredom strany.

Stredné priečky trojuholníka

Stredné priečky trojuholníka.

Sú to spojnice stredov dvoch strán a sú rovnobežné s treťou stranou trojuholníka. Veľkosť strednej priečky sa rovná polovičnej veľkosti strany trojuholníka, s ktorou je rovnobežná. Stredná priečka trojuholníka delí trojuholník na dve časti, ktorých obsahy sú v pomere 1 : 3

.

Kružnica opísaná trojuholníku

Kružnica opísaná trojuholníku.

Je to kružnica, ktorá obsahuje vrcholy daného trojuholníka. Stredom kružnice opísanej trojuholníku ABC je priesečník osí strán trojuholníka ABC. Polomer je spojnica stredu s ľubovoľným vrcholom.
Polomer opísanej kružnice:

R={\frac {a}{2\sin \alpha }}={\frac {b}{2\sin \beta }}={\frac {c}{2\sin \gamma }}

Kružnica vpísaná trojuholníku

Kružnica vpísaná trojuholníku.

Je to kružnica, ktorá sa dotýka všetkých strán daného trojuholníka. Stredom kružnice vpísanej trojuholníku ABC je priesečník osí uhlov trojuholníka ABC (a leží vždy vnútri trojuholníka!). Polomer je vzdialenosť stredu od ľubovoľnej strany trojuholníka.
Polomer vpísanej kružnice:

r=4R\cdot \sin {\frac {\alpha }{2}}\cdot \sin {\frac {\beta }{2}}\cdot \sin {\frac {\gamma }{2}}

alebo $r={\frac {2S}{o}}$ ; o = obvod trojuholníka, S = obsah trojuholníka

Osi strán

Priamky, ktoré prechádzajú stredom strán trojuholníka a sú na ne kolmé, nazývame osi strán. Pretínajú sa v jednom bode, ktorý je stredom opísanej kružnice (tento bod je rovnako vzdialený od všetkých vrcholov trojuholníka).

Osi vnútorných uhlov

Pretínajú sa v jednom bode, ktorý tvorí stred vpísanej kružnice (tento bod je rovnako vzdialený od všetkých strán trojuholníka).

Vzťahy platiace v trojuholníku

Výpočet obsahu

Vzorec pre výpočet obsahu trojuholníka vyzerá nasledovne: $S={\frac {av_{a}}{2}}={\frac {bv_{b}}{2}}={\frac {cv_{c}}{2}}$ pričom a, b, c sú strany trojuholníka a $v_{a}$ , $v_{b}$ , $v_{c}$ sú výšky kolmé na prislúchajúcu stranu.

Obsah však možno vypočítať aj Herónovým vzorcom: $S={\sqrt {s(s-a)(s-b)(s-c)}}$ , kde $s={\frac {o}{2}}$
Obsah trojuholníka pomocou vnútorného uhla: $S={\frac {1}{2}}ab\,\sin \gamma ={\frac {1}{2}}ac\,\sin \beta ={\frac {1}{2}}bc\,\sin \alpha$

Výpočet obvodu

Obvod trojuholníka sa rovná súčtu všetkých troch strán trojuholníka. Platí: $o=a+b+c$

Zhodnosť trojuholníkov

Dva trojuholníky môžu byť zhodné podľa troch viet o zhodnosti: sss, sus, usu.

Veta (sss): Každé dva trojuholníky, ktoré sa zhodujú vo všetkých troch stranách, sú zhodné.
Veta (sus): Každé dva trojuholníky, ktoré sa zhodujú v dvoch stranách a v uhle nimi určenom sú zhodné.
Veta (usu-suu): Každé dva trojuholníky, ktoré sa zhodujú v jednej strane a dvoch uhloch k nej priľahlých sú zhodné.
Veta (ssu): Každé dva trojuholníky, ktoré sa zhodujú v dvoch stranách a uhle ležiacom oproti väčšej z nich, sú zhodné.

Pravouhlý trojuholník

Pytagorova veta.

Pravouhlý trojuholník je špeciálny prípad trojuholníka, v ktorom platia špeciálne vzťahy (tieto vzťahy neplatia v ostatných 2 typoch trojuholníka.)
Vlastnosti pravouhlého trojuholníka

jeden z vnútorných uhlov má 90 stupňov
súčet ostatných dvoch ostrých uhlov je tiež 90 stupňov
pravouhlý trojuholník má dve odvesny a jednu preponu. Prepona je najdlhšia strana trojuholníka a je vždy oproti pravému uhlu.
keďže odvesny sú na seba kolmé, obsah pravouhlého trojuholníka možno vypočítať aj takto: ${\frac {ab}{2}}$ , kde a, b sú odvesny pravouhlého trojuholníka

Tálesova kružnica.

Vzťahy platiace v pravouhlom trojuholníku

Pytagorova veta: Obsah štvorca nad preponou pravouhlého trojuholníka sa rovná súčtu obsahov štvorcov nad oboma jeho odvesnami. Z toho vyplýva vzorec: $c^{2}=a^{2}+b^{2}$ .
Tálesova veta: Množina vrcholov pravých uhlov všetkých pravouhlých trojuholníkov s preponou AC je kružnica s priemerom AC s výnimkou bodov A a C.
Euklidova veta o výške: Obsah štvorca zostrojeného nad výškou pravouhlého trojuholníka spustenou na preponu sa rovná obsahu pravouholníka, ktorého strany sú úseky na prepone priľahlé k odvesnám.

v_{c}^{2}=c_{a}.c_{b}

Euklidova veta o odvesne: Obsah štvorca zostrojeného nad odvesnou pravouhlého trojuholníka sa rovná obsahu obdlžníka zostrojeného z prepony a úseku na prepone priľahlého k odvesne. Pre jednotlivé odvesny trojuholníka teda platí:

a^{2}=c.c_{a}

b^{2}=c.c_{b}

Pytagorova veta	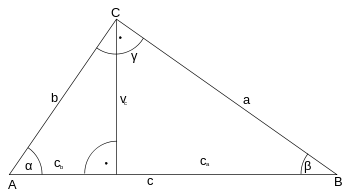$c^{2}=a^{2}+b^{2}$
Euklidova veta o odvesne	$a^{2}=c.c_{a}$
	$b^{2}=c.c_{b}$
	$c=c_{a}+c_{b}$
Euklidova veta o výške	$v_{c}^{2}=c_{a}.c_{b}$

Ďalšie vzťahy platiace v trojuholníkoch

Sínusová veta

Znenie sínusovej vety:

Pre každý trojuholník ABC s vnútornými uhlami α, β, γ a stranami a, b, c platí:

{\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}

Čiže:

Pomer všetkých dĺžok strán a hodnôt sínusov im protiľahlých uhlov je v trojuholníku konštantný.
Pomer dĺžok strán trojuholníka sa rovná pomeru sínusov im protiľahlých uhlov:

{\frac {a}{b}}={\frac {\sin \alpha }{\sin \beta }},\quad {\frac {b}{c}}={\frac {\sin \beta }{\sin \gamma }},\quad {\frac {c}{a}}={\frac {\sin \gamma }{\sin \alpha }}

Kosínusová veta

Kosínusová veta má tri základné varianty:

$a^{2}=b^{2}+c^{2}-2bc.cos\alpha$
$b^{2}=a^{2}+c^{2}-2ac.cos\beta$
$c^{2}=a^{2}+b^{2}-2ab.cos\gamma$

Referencie

Pozri aj

Iné projekty

Commons ponúka multimediálne súbory na tému Trojuholník
Wikislovník ponúka heslo Trojuholník

Externé odkazy

Obsah trojuholníka

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] ttp://mathworld.wolfram.com/EquilateralTriangle.html

[2] ttp://mathworld.wolfram.com/IsoscelesTriangle.html

[3] ttp://mathworld.wolfram.com/ScaleneTriangle.html