Euklidova veta

Ako Euklidove vety sa označujú dve matematické vety týkajúce sa pravouhlého trojuholníka. Pomenované sú po svojom objaviteľovi, gréckom matematikovi Eukleidovi z Alexandrie.

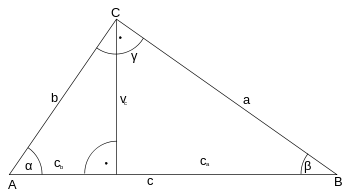
Obrázok s popísanými úsečkami vyskytujúcimi sa v Eukleidových vetách

Euklidova veta o výške

Obsah štvorca zostrojeného nad výškou pravouhlého trojuholníka sa rovná obsahu obdĺžnika zostrojeného z oboch úsekov na prepone.

Dôkaz pomocou Pytagorovej vety

 
   c = ca + cb
   vc2 = a2 - ca2
   vc2 = b2 - cb2

Rovnice sčítame:

   2vc2 = a2 + b2 - ca2 - cb2

Upravíme prvé 2 členy podľa Pytagorovej vety:

   2vc2 = c2 - ca2 - cb2

Rozpíšeme dĺžku prepony:

   c2 = (ca + cb)2

Dosadíme:

   2vc2 = (ca + cb)2 - ca2 - cb2
   2vc2 = ca2 + 2ca cb + cb2 - ca2 - cb2
   2vc2 = 2cacb

Vydelíme dvomi:

   vc2 = ca * cb

Euklidova veta o odvesne

Obsah štvorca zostrojeného nad odvesnou pravouhlého trojuholníka sa rovná obsahu obdlžníka zostrojeného z prepony a úseku na prepone priľahlého k odvesne. Pre jednotlivé odvesny trojuholníka teda platí:

Dôkaz pomocou Pytagorovej vety

 
   vc2 = a2 - ca2
   vc2 = b2 - (c - ca)2 = b2 - c2 + 2cca -ca2

Vytvoríme jednu rovnicu:

   a2 - ca2 = b2 - c2 + 2cca -ca2

Vyjadríme b2 - c2 pomocou a:

   a2 + b2 = c2
   b2 - c2 = -a2

Dosadíme:

   a2 = -a2 + 2cca
   2a2 = 2cca

Vydelíme dvomi:

   a2 = c * ca

Dôkaz pomocou Euklidovej vety o výške

Predpokladáme, že platí Euklidova veta o výške (dôkaz vyššie), z Pytagorovej vety vyplýva:

   a2 = vc2 + ca2
   a2 = ca cb + ca2
   a2 = (cb + ca) ca
   a2 = c * ca

Pozri aj
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.