Eliptická dráha
Eliptická dráha (alebo eliptická orbita), v astrodynamike alebo v nebeskej mechanike znamená Keplerovu dráhu s obežnou excentricitou menšou ako 1. Zahŕňa aj kruhovú dráhu s excentricitou rovnou nule. V striktnejšom chápaní je to Keplerova dráha s excentricitou väčšou ako 0 a menšou ako 1, zahŕňajúca kruhovú dráhu. V širšom zmysle je to Keplerova dráha s negatívnou energiou. Tá zahŕňa radiálnu eliptickú obežnú dráhu s excentricitou rovnajúcou sa 1.

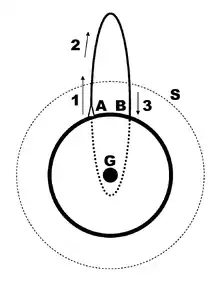
V gravitačnom probléme dvoch telies s negatívnou energiou, obidve telesá sa pohybujú po eliptickej obežnej dráhe s rovnakou dĺžkou doby obehu okolo spoločného barycentra. Tiež relatívna pozícia jedného telesa vzhľadom na druhé sa pohybuje po eliptickej obežnej dráhe.
Medzi eliptické obežné dráhy patria aj dvojeliptická prechodová dráha, Hohmannova prechodová dráha, a zvláštnym prípadom vysokej eliptickej dráhy sú Molnijova dráha a dráha Tundra. Medzi Eliptické dráhy patrí aj zotrvačná fáza suborbitálneho letu, ktorá prebieha po eliptickej dráhe, ale na rozdiel od klasických eliptických dráh pretína povrch obiehaného telesa.
Rýchlosť
Pri štandardnom predpoklade kruhová rýchlosť () telesa pohybujúceho sa po eliptickej dráhe je:
rýchlosť telesa vo vzdialenosti r je
kde:
- je štandardný gravitačný parameter,
- je vzdialenosť medzi obiehajúcimi telesami v mieste kde počítame v,
- je dĺžka veľkej polosi.
Rovnica rýchlosti pre hyperbolickú trajektóriu má navyše + , alebo je rovnaká, ale v tom prípade je záporná.
Obežná doba
Pri štandardnom predpoklade doba obehu () telesa pohybujúceho sa po eliptickej dráhe je:
kde:
- je štandardný gravitačný parameter,
- je dĺžka veľkej polosi.
Výsledok:
- Doba obehu je podobná tej pri kruhovej dráhe s obežným polomerom podobným strednej polosi ().
- Pre danú strednú polos obežná doba nezávisí na excentricite (pozri aj tretí Keplerov zákon).
Energia
Pri štandardnom predpoklade špecifická obežná energia () eliptickej dráhy je záporná a obežná energia pre danú obežnú dráhu môže byť:
kde:
- je rýchlosť obiehajúceho telesa,
- je vzdialenosť obiehajúceho telesa od centrálneho telesa,
- je dĺžka veľkej polosi,
- je štandardný gravitačný parameter.
Výsledok:
- Pre danú veľkú polos, špecifická obežná energia je nezávislá od excentricity.
Použitím vis-viva teórie zistíme:
- priemerný čas špecifickej potenciálnej energie je rovný 2ε,
- priemerný čas r−1 je a−1
- priemerný čas špecifickej kinetickej energie je rovný -ε,
Špecifický moment hybnosti
 Vektor polohy r, vektor rýchlosti v, skutočná anomália ν a uhol dráhy pohybu Φ na obežnej dráhe. Znázornené sú aj najdôležitejšie parametre elipsy (a, b, p).
Vektor polohy r, vektor rýchlosti v, skutočná anomália ν a uhol dráhy pohybu Φ na obežnej dráhe. Znázornené sú aj najdôležitejšie parametre elipsy (a, b, p).
kde:
- je špecifický relatívny moment hybnosti obežnej dráhy,
- je kruhová rýchlosť obiehajúceho telesa,
- je radiálna vzdialenosť obiehajúceho telesa od centrálneho telesa,
- je uhol dráhy pohybu,
- p je parametr elipsy, p = b2/a
Priemet dráhy na centrálne teleso

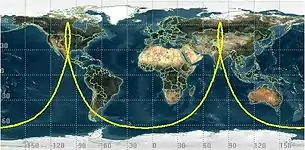

Priemet obežnej dráhy je zložený z pohybu obiehajúceho telesa a z vlastnej rotácie obiehaného telesa.
Kolmý priemet eliptickej dráhy na obiehané teleso má najčastejšie tieto tvary:
- bod – geostacionárna dráha s malou excentricitou
- úsečka – eliptická synchrónna dráha so sklonom 0°
- priamka – rovníková dráha, so sklonom 0°
- sínusoida – eliptické dráhy, so sklonom k rovníku a s malou excentricitou – typická pre bežné satelity s kruhovou orbitou
- cykloida – vysoké eliptické dráhy, so sklonom k rovníku cca 63°-116°a s excentrickou dráhou, s periódou pod 24hodin – typ Molnija
- osmičková – vysoké eliptické dráhy, so sklonom k rovníku cca 63°-116°a s veľkou excentricitou, s periódou 1deň – typ Tundra
Pozri aj
Externé odkazy
- Základy kozmických letov ⇒ orbitálna mechanika (po anglicky)
- Mesačné fotografické porovnania (po anglicky)
- Afélium - Perihélion (po anglicky)
- Tundra_Orbits.wmv (po anglicky)
Zdroj
- D’ELISEO, MM. The first-order orbital equation. American Journal of Physics, 2007, s. 352 – 355. DOI: 10.1119/1.2432126.
- D’ELISEO, MM. The gravitational ellipse. Journal of Mathematical Physics, 2009, s. 022901-022901-10 doi = 10.1063/1.3078419.
Tento článok je čiastočný alebo úplný preklad článku Elliptic orbit na anglickej Wikipédii.
