Barycentrum

Barycentrum je v astronómii centrum hmoty dvoch alebo viacerých telies, ktoré sa obiehajú navzájom a je bodom, okolo ktorého tieto telesá obiehajú. Je to dôležitá koncepcia v oblastiach astronómie a astrofyziky. Vzdialenosť od stredu hmoty telesa k barycenteru sa môže vypočítať ako problém dvoch telies.

Pohyb Slnka okolo barycentra Slnečnej sústavy v rokoch 2000 až 2050, pozícia Slnka je k 19. jún 2025 pri 24. perihélium sondy Parker Solar Probe.

Problém dvoch telies

Problém dvoch telies je úloha klasickej mechaniky, v ktorej je cieľom skúmať pohyb dvoch telies, ktoré navzájom interagujú. Príkladom môže byť obeh planét okolo Slnka.

V prípade dvoch telies vzdialenosť r1 od ťažiska primárneho telesa (hmotnosti m1) k barycenteru je daná:

r_{1}=a\cdot {\frac {m_{2}}{m_{1}+m_{2}}}={\frac {a}{1+{\frac {m_{1}}{m_{2}}}}}

r1 je vzdialenosť ťažiska telesa 1 k barycenteru
a je vzdialenosť medzi ťažiskami oboch telies
m1 a m2 sú hmotnosti oboch telies.

V nasledujúcej tabuľke sú uvedené niektoré príklady telies zo slnečnej sústavy. R1 je polomer centrálneho telesa, M_⊕ hmotnosť Zeme.

Centrálne	m₁(`M`_⊕)	Obiehajúce	m₂(`M`_⊕)	a(km)	r₁(km)	R₁(km)	r₁/R₁
Zem	1	Mesiac	0.0123	384,000	4,670	6,380	0.732
Pluto	0.0021	Charon	0.000254 (0.121 M_♇)	19,600	2,110	1,150	1.83
Slnko	333,000	Zem	1	150,000,000 (1 AU)	449	696,000	0.000646
Slnko	333,000	Jupiter	318 (0.000955 `M`_☉)	778,000,000 (5.20 AU)	742,000	696,000	1.07

Problém n telies

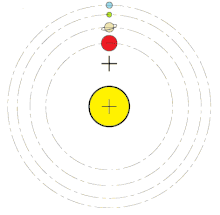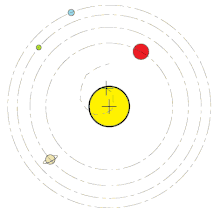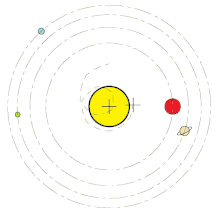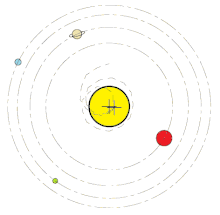
Barycentrum slnečnej sústavy - vplyv planét (Slnko s barycentrom sú zobrazené v mierke, planéty sú znázornené schématicky)

Ak chcete vypočítať barycentrum Slnečnej sústavy a skutočný pohyb Slnka, stačí zvážiť pohyby štyroch veľkých planét (Jupiter, Saturn, Urán, Neptún). Príspevky všetkých ostatných planét, trpasličích planét atď. sú zanedbateľné. Ak by štyri obrie planéty boli na rovnej línii na tej istej strane Slnka, centrum hmoty Slnečnej sústavy by ležalo o viac ako 810 000 km nad povrchom Slnka, teda okolo 1,17 násobku polomeru Slnka nad jeho povrchom. V prípade ak sa vplyvy planét vzájomne vykompenzujú, bude barycentrum ležať pri ťažisku Slnka.

Barycentrum sústavy Zem-Mesiac; vzhľadom na pomer hmotností obidvoch telies (81:1) leží vnútri Zeme.

Zdroje

Tento článok je čiastočný alebo úplný preklad článku Barycenter na anglickej Wikipédii.

Tento článok alebo jeho časť obsahuje heslo z Encyklopédie astronómie s láskavým dovolením autorov a podporou SZA.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.