Dvojeliptická prechodová dráha

Dvojeliptická prechodová dráha (al. bieliptická dráha) v astrodynamike alebo v nebeskej mechanike znamená prechodovú dráhu z nízkej kruhovej orbity na vysokú kruhovú orbitu, zloženú z dvoch polovíc eliptických dráh. Tieto eliptické dráhy sa dotýkajú hlavnými vrcholmi elipsy a druhé hlavné vrcholy ležia na nízkej a vysokej kruhovej orbite, pričom obiehané teleso sa nachádza v ohnisku elíps podľa Keplerových zákonov. Zvláštnosťou tejto prechodovej dráhy je, že prechodová dráha leží vysoko nad cieľovou orbitou.

Táto dráha môže byť za určitých podmienok energeticky efektívnejšia ako Hohmannova prechodová dráha. Myšlienku dvojeliptickej prechodovej dráhy publikoval v roku 1934 Ary Sternfeld.[1]

Princíp dvojeliptickej prechodovej dráhy
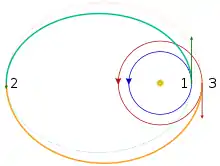
Dvojeliptická prechodová dráha pre prechod z nízkej kruhovej orbity (modrá), na vysokú kruhovú orbitu (červená)

Obiehajúce teleso aktívne prechádza z nízkej kruhovej orbity (na obrázku modrá), na vysokú kruhovú orbitu (červená), nasledovným postupom:

  • 1/ teleso zvýši obežnú rýchlosť, čím zmení svoju dráhu na vysokú eliptickú, s apogeom nad cieľovou orbitou (prvá poloelipsa - na obrázku zelená)
  • 2/ teleso v apogeu zvýši rýchlosť tak, aby nová dráha mala v perigeu výšku zhodnú s kruhovou dráhou, na ktorú sa prechádza (druhá poloelipsa - na obrázku oranžová)
  • 3/ teleso po dosiahnutí cieľovej orbity pribrzdí, čím cirkularizuje dráhu


Príklad

Ak chceme preniesť družicu z nízkej kruhovej orbity s polomerom r 0 = 6700 km na novú kruhovú dráhu s polomerom r 1 = 93800 km, potom pomocou Hohmannovej prechodovej dráhy bude potrebné delta - v = 2.824,34 + 1.308,38 = 4132,72 m /s. Ale pri splnení podmienky r 1 > 11,94 r 0 , čo spĺňame, je energeticky výhodnejšie použiť bi-eliptickú dráhu . Ak sa družica najprv urýchli o 3060,31 m/s , čím sa dostane na eliptickú obežnú dráhu s apogeom 268000 km ( r 2 = 40 r 0 ). Následne sa v apogeu urýchľuje o ďalších 608,679 m/s, čím zmení obežnú dráhu na dráhu s novým perigeom r 1 = 93800 km. Na záver , v apogeu pribrzdí o 447,554 m/s, čím cirkularizuje konečnú dráhu. Potom celkové delta - v bude iba 4116,54 , čo je o 16,18 m/s ( 0,4 % ) menej, ako pri Hohmanovej dráhe. Nevýhodou je ale nepomerne dlhší čas prechodu na novú dráhu.

! ZápalHohmanova dráha delta v (m/s)Dvoj eliptická dráha delta v (m/s)
12824,343060,31
21308,38608,679
3-447,554
Spolu 4132,72 4.116,54
  • Zelená ⇒ delta v, prírastok orbitálnej rýchlosti aplikovaný prográdne
  • Červená ⇒ delta v, aplikovaná retrográdne - zníženie orbitálnej rýchlosti


Lepšia efektivita dvojeliptickej prechodovej dráhy (voči Hohmanovej dráhe) spočíva vo vyššom prírastku delta v v perigeu, čím sa využíva Oberthov efekt.

Pozri aj


Referencie
  1. Sternfeld, Ary J. [sic] (1934-02-12), "Sur les trajectoires permettant d'approcher d'un corps attractif central à partir d'une orbite keplérienne donnée" [On the allowed trajectories for approaching a central attractive body from a given Keplerian orbit], Comptes rendus de l'Académie des sciences (in French) (Paris) 198 (1): 711–713

Zdroj

Tento článok je čiastočný alebo úplný preklad článku Bi-elliptic transfer na anglickej Wikipédii.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.