Obor hodnot

• Funkce sinus ${\displaystyle \scriptstyle \sin$ :\mathbb {R} \rightarrow \mathbb {R} } nabývá pouze hodnot mezi -1 a 1, a proto je její obor hodnot ${\displaystyle \scriptstyle {\mathcal {H}}(\sin )}$ interval ${\displaystyle \scriptstyle \left\langle -1,1\right\rangle }$.
• Oborem hodnot absolutní hodnoty čísla jsou všechna nezáporná reálná čísla.
• Oborem hodnot nemusí být jen čísla, lze sestrojit zobrazení, které vezme číslo a vrátí zobrazení. Uvažme například zobrazení ${\displaystyle \scriptstyle T}$, které vezme číslo ${\displaystyle \scriptstyle a\in \mathbb {R} }$ a vrátí zobrazení ${\displaystyle \scriptstyle f(x)=\exp(ax)}$. Neboli

${\displaystyle T:\mathbb {R} \to {\mathcal {C}},}$

kde ${\displaystyle \scriptstyle {\mathcal {C}}}$ označuje množinu spojitých funkcí definovaných na ${\displaystyle \scriptstyle \mathbb {R} }$. Hodnotou zobrazení ${\displaystyle \scriptstyle T}$ je tedy opět nějaké zobrazení ${\displaystyle \scriptstyle f}$, které zobrazuje reálná čísla na kladná reálná čísla, tj. ${\displaystyle \scriptstyle f:\mathbb {R} \to \mathbb {R} ^{+}}$.

Mějme zobrazení ${\displaystyle \scriptstyle T:X\to Y}$. V závislosti na tom, zda zobrazení ${\displaystyle \scriptstyle T}$ při svém působení na množinu ${\displaystyle \scriptstyle X}$ vyčerpá všechny prvky množiny ${\displaystyle \scriptstyle Y}$, nebo ne, se zavádí následující názvosloví:

• Pokud pro každý prvek ${\displaystyle \scriptstyle y}$ množiny ${\displaystyle \scriptstyle Y}$ existuje prvek ${\displaystyle \scriptstyle x}$ z množiny ${\displaystyle \scriptstyle X}$ takový, že ${\displaystyle \scriptstyle T(x)=y}$, tak nazýváme zobrazení ${\displaystyle \scriptstyle T}$ surjektivní zobrazení, neboli říkáme, že zobrazení ${\displaystyle \scriptstyle T}$ zobrazuje množinu ${\displaystyle \scriptstyle X}$ na množinu ${\displaystyle \scriptstyle Y}$.
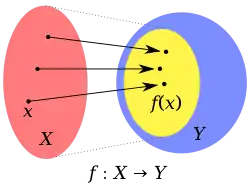
• Pokud naopak existuje prvek ${\displaystyle \scriptstyle y}$ z množiny ${\displaystyle \scriptstyle Y}$, pro něž nenajdeme jeho vzor v množině ${\displaystyle \scriptstyle X}$, tak říkáme, že zobrazení ${\displaystyle \scriptstyle T}$ zobrazuje množinu ${\displaystyle \scriptstyle X}$ do množiny ${\displaystyle \scriptstyle Y}$. Tomuto případu odpovídá situace na obrázku. Tam je žlutou barvou vyznačen obor hodnot zobrazení (funkce) ${\displaystyle \scriptstyle f}$, zatímco modrou barvou jsou vyznačeny ty prvky množiny ${\displaystyle \scriptstyle Y}$, pro něž neexistuje odpovídající ${\displaystyle \scriptstyle x\in X}$, pro které by platilo ${\displaystyle \scriptstyle T(x)=y}$. Uvedeného pojmu zobrazovat do množiny se užívá i případě, kdy se nestaráme o to, zda ${\displaystyle \scriptstyle T}$ skutečně nepokryje celou množinu ${\displaystyle \scriptstyle Y}$ a připouštíme tak obě možnosti, tj. i tu, kdy je zobrazení ${\displaystyle \scriptstyle T}$ surjektivní.

Ve funkcionální analýze se zavádí pojem esenciálního oboru hodnot. Buď ${\displaystyle \scriptstyle M}$ množina vybavená mírou ${\displaystyle \scriptstyle \mu }$ a nechť ${\displaystyle \scriptstyle f}$ je nějaká komplexní funkce definovaná na ${\displaystyle \scriptstyle M}$, tj. ${\displaystyle \scriptstyle f:M\to \mathbb {C} }$. Pak pod pojmem esenciální obor hodnot funkce ${\displaystyle \scriptstyle f}$ rozumíme množinu

${\displaystyle R_{\text{ess}}(f)=\{\lambda \in \mathbb {C} |(\forall \epsilon >0)(\mu (M_{\epsilon }(\lambda ))>0)\},\quad {\text{kde}}\quad M_{\epsilon }(\lambda )=\{x\in M|\ |f(x)-\lambda |<\epsilon \}.}$

• BLANK, Jiří; EXNER, Pavel; HAVLÍČEK, Miloslav. Lineární operátory v kvantové fyzice. Praha: Karolinum, 1993. ISBN 80-7066-586-6.

• Definiční obor
• Omezená funkce