Zobrazení (matematika)
Zobrazení je v matematice předpis, kterým se prvkům určité množiny X přiřazuje nejvýše jeden prvek množiny Y. Přesněji mluvíme o zobrazení z množiny X do množiny Y. Pokud X=Y, mluvíme o zobrazení na množině. Ve speciálním případě, když je Y libovolná číselná množina, zobrazení nazýváme funkcí. Je-li prvku x množiny X přiřazen prvek y množiny Y, pak říkáme, že x je vzorem a y je obrazem.

Matematicky je zobrazení speciálním případem binární relace, u které má každý vzor nejvýše jeden obraz.
Zobrazení z množiny do množiny
Nejobecnějším z hlediska množin, do kterých náleží vzory a obrazy, je zobrazení z množiny do množiny.
- Definice[1]
Zobrazení z množiny do množiny je taková binární relace, pro kterou platí, že ke každému prvku množiny přiřazuje nejvýše jeden takový prvek množiny tak, že .
- Značení[1]
nebo
- Důležité pojmy[1]
- Prvek se nazývá obrazem prvku v zobrazení nebo také hodnotou zobrazení v bodě . Podobně obraz množiny v zobrazení je množina , na kterou se zobrazí :
- Prvek se nazývá vzorem prvku v zobrazení . Podobně vzor množiny v zobrazení je množina obsahující všechny prvky, které se do množiny zobrazí; značí se
- Množina právě těch prvků , pro které existuje prvek , že , se nazývá definičním oborem zobrazení (též zkráceně oborem zobrazení či úplným vzorem zobrazení). Je to tedy množina všech vzorů. Značí se zpravidla jednou ze značek .
- Množina právě těch prvků , pro které existuje aspoň jeden takový prvek , že , se nazývá oborem hodnot zobrazení (též úplným obrazem zobrazení). Je to tedy množina všech obrazů, respektive obraz celého definičního oboru. Značí se zpravidla jednou ze značek .
V teorii množin se tedy zobrazení definuje jako binární relace splňující podmínku existence a jednoznačnosti:
- .
Typy zobrazení
Podle pokrytí výchozí a cílové množiny
- Zobrazení v množině[1]
Zobrazení v množině je takové zobrazení z množiny do množiny , pro které , tedy výchozí a cílová množina jsou totožné.
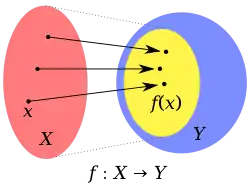
Zobrazení množiny do množiny je takové zobrazení z množiny do množiny , pro které . Definičním oborem je tedy celá výchozí množina. Tedy ke každému prvku existuje (právě jeden) takový prvek , že .
Značí se:
Zobrazení z množiny na množinu neboli surjektivní zobrazení (surjekce) je takové zobrazení z množiny do množiny , pro které . Zobrazuje tedy definiční obor na celou cílovou množinu. Tedy ke každému prvku existuje aspoň jeden takový prvek , že .
Zobrazení množiny na množinu je takové zobrazení z množiny do množiny , pro které . Tedy ke každému prvku existuje právě jeden takový prvek , že , a ke každému prvku existuje aspoň jeden takový prvek , že .
- Zobrazení na množině[1]
Zobrazení na množině je takové zobrazení množiny na množinu , pro které , tedy výchozí a cílová množina jsou totožné.
Zobrazení prosté, vzájemně jednoznačné a inverzní
Zobrazení f z množiny do množiny se nazývá prosté neboli injektivní zobrazení (injekce), právě když každé dva různé vzory mají různé obrazy :
Vzájemně jednoznačné zobrazení množin a neboli bijektivní zobrazení (bijekce) je prostým zobrazením množiny na množinu , je tedy injektivní a surjektivní zároveň.
Značí se:
Je-li prosté zobrazení z množiny do množiny , pak zobrazení z množiny do množiny , které každému přiřazuje ten prvek , pro nějž , se nazývá inverzní zobrazení k zobrazení . Jeho definičním oborem je tedy a platí .
Podle druhu vzorů a obrazů
Například:
- Posloupnost je zobrazení z množiny přirozených čísel (zpravidla do jiné číselné množiny, v obecném smyslu i do jiných druhů objektů) – vzor udává pořadí obrazu.
- Funkce (reálné či komplexní proměnné) je zobrazení v množině reálných či komplexních čísel.
- Vektorová, tenzorová resp. maticová funkce je zobrazení z množiny (vektorového prostoru) vektorů, tenzorů resp. matic.
- Funkcionál zobrazuje funkci na číslo.
- Operátor - funkci přiřazuje funkci.
- Třídové zobrazení - vzory i obrazy jsou množiny či třídy.
Další speciální typy
Například:
- Totožnost (identita) - každému prvku přiřadí tentýž prvek.
- Spojité zobrazení - k blízkým vzorům přiřazuje blízké obrazy.
- Lineární zobrazení - platí pro něj , kde a jsou prvky daného tělesa a a jsou prvky vektorového prostoru nad tímto tělesem.
- Konformní zobrazení - spojité zobrazení, které zachovává úhly.
Příklad zobrazení
Mějme množiny a . Můžeme například definovat zobrazení jako
Oborem hodnot je tedy množina . Vzorem množiny je množina . Jeden prvek v tedy může mít více než jeden vzor v . Ale každý prvek se zobrazí na právě jeden prvek v .
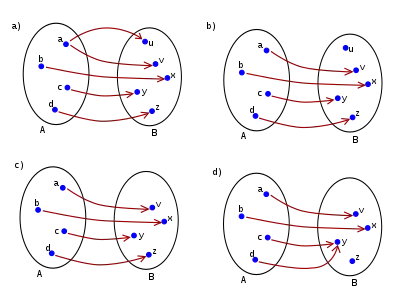
Na obrázku jsou uvedeny příklady vztahů .
- Na a) je příklad, kdy se nejedná o zobrazení.
- Na b) je příklad prostého zobrazení množiny do množiny .
- Na c) je vzájemně jednoznačné zobrazení na .
- Na d) je zobrazení, které není prosté.
Víceznačné zobrazení
Jak vyplývá z uvedené definice zobrazení, název víceznačné zobrazení je matematický oxymóron. Pojem se ale běžně užívá pro relaci, kde každému vzoru odpovídá alespoň jeden obraz. Víceznačné zobrazení
lze převést na běžné jednoznačné zobrazení do potenční množiny B
Víceznačná zobrazení jsou poměrně přirozený způsob, jak se vypořádat s inverzí od zobrazení, které není prosté. Například
Reference
- BARTSCH, Hans-Jochen, 1983. Matematické vzorce. Překlad TICHÝ, Zdeněk. 1. české (podle 17. originálního). vyd. Praha: SNTL – Nakladatelství technické literatury. 832 s. 04-020-83. Kapitola 0.4.6 Zobrazení, operace, funkce, s. 83–86.
- REKTORYS, Karel, a kol. Přehled užité matematiky. 4.. vyd. Praha: SNTL – Nakladatelství technické literatury, 1981. 1140 s. 04-003-81. Kapitola 1.23 Pojem množiny a pojem zobrazení, s. 73.
- Bartsch 1983, s. 87.