Kuželosečka

Kuželosečka je rovinná křivka, která vznikne jako průnik roviny s rotační kuželovou plochou, přičemž rovina neprochází jejím vrcholem.

Druhy kuželoseček

Typy kuželoseček

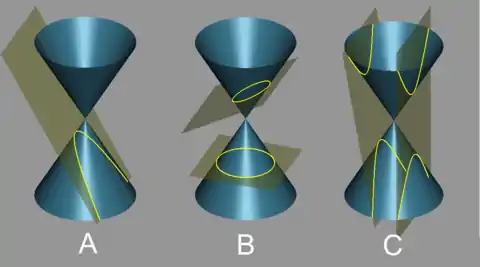
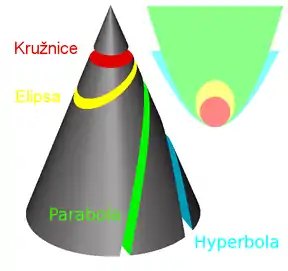
Protínáme-li kužel rovinou kolmou na osu symetrie rotačního kuželu, výslednou kuželosečkou je kružnice.

Protínáme-li kužel rovinou rovnoběžnou právě s jednou z povrchových přímek pláště kuželu, výslednou kuželosečkou je parabola.

Protínáme-li kužel rovinou, která svírá s osou symetrie rotačního kuželu úhel menší než 90° a větší než polovina vrcholového úhlu kuželu, výslednou kuželosečkou je elipsa. Rovina přitom protíná všechny povrchové přímky pláště kužele a není tedy s žádnou z nich rovnoběžná.

Protínáme-li kužel rovinou, která svírá s osou symetrie rotačního kuželu úhel menší než polovina vrcholového úhlu kuželu, výslednou kuželosečkou je hyperbola; přitom rovina je rovnoběžná právě se dvěma povrchovými přímkami kuželu.

(A: parabola, B: elipsa a kružnice, C: hyperbola)

Degenerované kuželosečky

Za kuželosečku bývá často považován také průnik kuželové plochy s rovinou procházející vrcholem kuželové plochy. Takovéto kuželosečky označujeme jako degenerované (nevlastní, singulární), neboť podle polohy roviny a osy kuželové plochy dochází k redukci kuželosečky na bod, přímku nebo dvě přímky.

Kuželosečky, které nejsou degenerované, tzn. kružnici, elipsu, parabolu a hyperbolu, označujeme jako vlastní (regulární) kuželosečky.

Algebraické vyjádření

Každou kuželosečku lze vyjádřit rovnicí

a_{11}x^{2}+2a_{12}xy+a_{22}y^{2}+2a_{13}x+2a_{23}y+a_{33}=0

,

kde koeficienty $a_{ij}$ jsou reálná čísla, přičemž $a_{ij}=a_{ji}$ . Tato rovnice je algebraickou rovnicí druhého stupně v $x$ a $y$ .

Invarianty

Při transformaci souřadnic se nemění některé charakteristické veličiny algebraické rovnice kuželosečky. Tyto veličiny se označují jako invarianty.

Uvedená rovnice má tři invarianty:

determinant kuželosečky

\Delta ={\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}}

determinant kvadratických členů

\delta ={\begin{vmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{vmatrix}}

třetím invarientem je stopa malé matice

S=a_{11}+a_{22}

Při transformaci souřadnic se tedy mění koeficienty $a_{ij}$ , avšak uvedené invarianty se nezmění.

Klasifikace kuželoseček podle invariantů

Invarianty rovnice kuželosečky lze použít ke klasifikaci jednotlivých křivek, které jsou touto rovnicí určeny.

Je-li $\Delta \neq 0$ , pak se jedná o vlastní kuželosečku. Pro $\Delta =0$ jde o kuželosečku degenerovanou. Rovnicemi s $\delta =0$ jsou určeny tzv. nestředové kuželosečky (např. parabola). Pro $\delta \neq 0$ se jedná o kuželosečky středové (např. elipsa).

Rozdělení kuželoseček	$\delta \neq 0$ středové kuželosečky		$\delta =0$ nestředové kuželosečky
	$\delta >0$	$\delta <0$
$\Delta \neq 0$ vlastní kuželosečky	$\Delta S<0$ reálná elipsa	hyperbola	parabola
	$\Delta S>0$ imaginární elipsa
$\Delta =0$ nevlastní kuželosečky	dvojice nerovnoběžných (protínajících se) imaginárních přímek s reálným průsečíkem	dvě reálné různoběžky	$a_{13}^{2}-a_{11}a_{33}<0$ dvě různé reálné rovnoběžky	$a_{13}^{2}-a_{11}a_{33}=0$ dvě splývající rovnoběžky	$a_{13}^{2}-a_{11}a_{33}>0$ dvě imaginární rovnoběžky

Středové rovnice kuželoseček

Kružnice: $(x-m)^{2}+(y-n)^{2}=r^{2}$

Elipsa: ${\frac {(x-m)^{2}}{a^{2}}}+{\frac {(y-n)^{2}}{b^{2}}}=1$

Parabola: $(x-m)^{2}=2p(y-n)$

Hyperbola: ${\frac {(x-m)^{2}}{a^{2}}}-{\frac {(y-n)^{2}}{b^{2}}}=1$

Výskyt a použití kuželoseček

Kuželosečky mají praktické uplatnění v architektuře, optice, radiotechnice, astronomii a dalších oborech. Vlnění vycházející libovolným směrem z jednoho ohniska elipsy (nebo rotační eliptické plochy) je odráženo do druhého ohniska; této skutečnosti se využívá při výrobě laserů[1] a při vytváření tak zvaných šeptajících galerií, kdy slova šeptaná v jednom ohnisku klenby nebo zakřivené stěny jsou dobře slyšitelná pouze ve vzdáleném druhém ohnisku. Vlnění vycházející z ohniska paraboly je odráženo jako svazek rovnoběžných paprsků stejným směrem, čehož se využívá při výrobě světlometů, dalekohledů, parabolických antén a radioteleskopů. Pomocí parabolického zrcadla se zapaluje Olympijský oheň. Opominutí vlastností kuželoseček může vést k požárům, zraněním nebo poškozování věcí.[2]

Řešením nejjednodušší úlohy nebeské mechaniky – pohybu hmotného bodu v gravitačním poli centrálního tělesa – jsou kuželosečky. V prvním přiblížení lze pohyb planet, asteroidů, komet a meziplanetárních sond okolo Slunce, stejně jako pohyb přirozených i umělých satelitů okolo planet popsat jako pohyb lehčího objektu po kuželosečce okolo hmotnějšího objektu, viz Keplerovy zákony.

Odkazy

Reference

REICHL, Jaroslav; VŠETIČKA, Martin. Lasery využívající pevné látky [online]. Dostupné online.
Londýnský parabolický mrakodrap ničí auta, roztavil jaguára či dodávku [online]. MAFRA a.s., 2013-09-03. Dostupné online.

Literatura

Šárka Voráčová a kolektiv: Atlas geometrie – Geometrie krásná a užitečná, Academia, Praha 2012, ISBN 978-80-200-1575-4, str. 112-113

Související články

Externí odkazy

Obrázky, zvuky či videa k tématu kuželosečka na Wikimedia Commons

Slovníkové heslo kuželosečka ve Wikislovníku
Kuželosečky (pdf)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] REICHL, Jaroslav; VŠETIČKA, Martin. Lasery využívající pevné látky [online]. Dostupné online.

[2] Londýnský parabolický mrakodrap ničí auta, roztavil jaguára či dodávku [online]. MAFRA a.s., 2013-09-03. Dostupné online.