Průnik
V matematice se jako průnik dvou nebo více množin označuje taková množina, která obsahuje pouze ty prvky, které se nalézají ve všech těchto množinách. Průnik množin A a B se označuje symbolem A ∩ B.
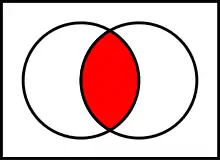
Formální definice
Pro všechna x platí, že .
V případě, že se jedná o průnik více množin, je možno jej chápat jako několik postupných průniků (viz asociativita níže), nebo tak, že prvek je součástí průniku právě tehdy, je-li prvkem všech množin. Obě tyto možnosti jsou však ekvivalentní. Např. pro průnik tří množin platí, že x ∈ A ∩ B ∩ C iff x ∈ A a zároveň x ∈ B a zároveň x ∈ C. Průnik množin lze zkráceně psát
Příklad: Průnikem množin { 1, 2, 5, 6, 8, 11 } a { 2, 3, 4, 6, 8, 9 } je množina { 2, 6, 8 }. Průnikem množin všech prvočísel { 2, 3, 5, 7, 11, … } a množiny sudých kladných čísel { 2, 4, 6, 8, … } je jednoprvková množina { 2 } (jelikož 2 je jediné sudé prvočíslo).
Vlastnosti
Operace průniku dvou množin (jakožto binární operace) je asociativní, tzn. (A ∩ B) ∩ C = A ∩ (B ∩ C). Současný průnik všech tří množin – A ∩ B ∩ C – je oběma těmto výrazům roven, proto je možno psát průnik libovolného množství množin bez použití závorek.
Průnik je komutativní operace, platí tedy, že A ∩ B = B ∩ A.
Neutrálním prvkem pro operaci průniku je univerzum, tzn. množina všech prvků, které v daném kontextu uvažujeme. Platí tedy .
Výsledkem průniku množiny s prázdnou množinou je opět prázdná množina, tzn. .
Je-li výsledkem průniku dvou množin prázdná množina, pak platí , kde je doplňkem množiny .
Vzhledem k definici průniku vyplývají všechny tyto skutečnosti z obdobných skutečností o logické spojce a zároveň.
Mohutnost průniku dvou množin je nejvýše rovna mohutnosti menší z nich: |A ∩ B| ≤ min { |A|, |B| }.
Průnik je idempotentní, tzn. platí .