Hindsko-arabská číselná soustava

Hindsko-arabská číselná soustava[1] nebo také hindská číselná soustava[2], poziční desítková číselná soustava, je celosvětově nejrozšířenější systém pro symbolickou reprezentaci čísel. Soustava byla vynalezena indickými matematiky mezi 1. a 4. stoletím. Tento systém byl přijat perskými matematiky (Al-Chorezmího kniha O výpočtech s hindskými číslicemi kolem r. 825) a arabskými matematiky (Al-Kindího kniha O používání hindských číslic kolem r. 825) v 9. století. Později se soustava rozšířila do Evropy vrcholného středověku.

Systém je založen na deseti (původně devíti) rozdílných glyfech. Symboly (glyfy) použité tak, aby reprezentovaly soustavu, jsou v zásadě nezávislé na samotném systému. Znaky aktuálně používané vychází z brahmánských číslic a už od středověku se rozdělují na různé typografické varianty.

Tyto symboly lze rozdělit do tří hlavních skupin: arabské číslice používané v oblasti velkého Maghrebu a v Evropě, východoarabské číslice (také nazývané „indické číslice“) používané na středním Východě a indické číslice používané na indickém subkontinentu.

Tato číselná soustava se dodnes používá po celém světě.

Etymologie

Hindsko-arabské číslice byly vynalezeny matematiky v Indii. Persko-arabští matematici je nazývali „hindské číslice“ (kde „hindský“ znamená indický). Později se jim v Evropě začalo říkat „arabské číslice“, protože na Západě byly představeny arabskými obchodníky.[3]

Porovnání znaků
0123456789písmoviz
○/零一二三四五六七八九východní Asiečínské, japonské, korejské číslice
ο/ōΑʹΒʹΓʹΔʹΕʹϚʹΖʹΗʹΘʹnovořečtinařecké číslice
 אבגדהוזחטhebrejštinahebrejské číslice
०१२३४५६७८९dévanágaríindické číslice
૦૧૨૩૪૫૬૭૮૯gudžarátština
੦੧੨੩੪੫੬੭੮੯gurmukhí
༠༡༢༣༤༥༦༧༨༩tibetština
০১২৩৪৫৬৭৮৯ásámsky/ bengálsky/ sylheti Bengálsko-ásámské číslice
୦୧୨୩୪୫୬୭୮୯orija
൦൧൨൩൪൫൬൭൮൯malajálamština
௦ ௧ ௨ ௩ ௪ ௫ ௬ ௭ ௮ ௯ tamilsky tamilské číslice
0౧౨౩౪౫౬౭౮౯telugština
೦೧೨೩೪೫೬೭೮೯kannadština
០១២៣៤៥៦៧៨៩khmerskykhmerské číslice
๐๑๒๓๔๕๖๗๘๙thajskythajské číslice
໐໑໒໓໔໕໖໗໘໙laosky
၀၁၂၃၄၅၆၇၈၉barmština
٠‎ ١‎ ٢‎ ٣‎ ٤‎ ٥‎ ٦‎ ٧‎ ٨‎ ٩‎ arabština arabské číslice
۰‎ ۱‎ ۲‎ ۳‎ ۴‎ ۵‎ ۶‎ ۷‎ ۸‎ ۹‎ perské písmo (farsí)/ darí/ paštština
urdsky/ shahmukhi

Stejně jako v mnoha systémech číslování, číslice 1, 2 a 3 představují jednoduché záznamy značek; 1 je jedna čára, 2 jsou dvě čáry (nyní spojené úhlopříčkou) a 3 jsou tři čáry (nyní spojené dvěma svislými čarami). Po třech číslech symboly mají tendenci se stát složitějšími (příkladem jsou čínské číslice a římské číslice). Teoretici věří, že je to proto, že je obtížné okamžitě počítat předměty o větším počtu než tři.[4]

Historie
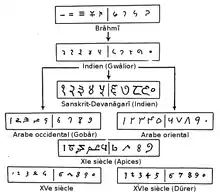
Odvození moderních číslic z brahmánského zápisu

Odkazy

Reference

V tomto článku byl použit překlad textu z článku Hindu–Arabic_numeral_system na anglické Wikipedii.

  1. David Eugene Smith and Louis Charles Karpinski, The Hindu–Arabic Numerals, 1911
  2. William Darrach Halsey, Emanuel Friedman. Collier's Encyclopedia, with bibliography and index. [s.l.]: [s.n.], 1983. Dostupné online. (anglicky)
  3. ROWLETT, Russ. Roman and "Arabic" Numerals. [s.l.]: University of North Carolina at Chapel Hill, 2004-07-04. Dostupné v archivu pořízeném dne 2018-07-31. (anglicky)
  4. Language may shape human thought Archivováno 17. 4. 2008 na Wayback Machine, New Scientist, news service, Celeste Biever, 19:00 19 August 2004.

Související články

Externí odkazy

Bibliografie
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.