Násobení matic

Pokud A je matice o rozměrech m × n a B je matice n × p, jejich součin ${\displaystyle A\cdot B}$ je matice s rozměry m × p definována vztahem

${\displaystyle (A\cdot B)_{ij}=\sum _{r=1}^{n}a_{ir}b_{rj}=a_{i1}b_{1j}+a_{i2}b_{2j}+\cdots +a_{in}b_{nj}.}$

pro všechny prvky (i , j) výsledné matice.

Prvek v i-tém řádku a j-tém sloupci výsledné matice lze také chápat jako skalární součin vektoru i-tého řádku první matice s vektorem j-tého sloupce druhé matice.

Tečka ${\displaystyle \cdot }$ se obvykle vynechává a píše se pouze ${\displaystyle AB}$.

Ilustrační obrázek

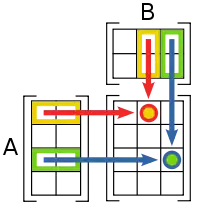
Mají se znásobit matice: ${\displaystyle \mathbf {A} ={\begin{pmatrix}\color {blue}1&\color {blue}2&\color {blue}3\\\color {orange}4&\color {orange}5&\color {orange}6\\\end{pmatrix}},\mathbf {B} ={\begin{pmatrix}\color {red}1&\color {green}2\\\color {red}3&\color {green}4\\\color {red}5&\color {green}6\\\end{pmatrix}}.}$ Jejich součin je

${\displaystyle \mathbf {A} \cdot \mathbf {B} ={\begin{pmatrix}({\color {blue}1}\cdot {\color {red}1}+{\color {blue}2}\cdot {\color {red}3}+{\color {blue}3}\cdot {\color {red}5})&({\color {blue}1}\cdot {\color {green}2}+{\color {blue}2}\cdot {\color {green}4}+{\color {blue}3}\cdot {\color {green}6})\\({\color {orange}4}\cdot {\color {red}1}+{\color {orange}5}\cdot {\color {red}3}+{\color {orange}6}\cdot {\color {red}5})&({\color {orange}4}\cdot {\color {green}2}+{\color {orange}5}\cdot {\color {green}4}+{\color {orange}6}\cdot {\color {green}6})\\\end{pmatrix}}={\begin{pmatrix}22&28\\49&64\end{pmatrix}}}$

(Tj. prvky matice A zůstávají v řádcích tak, jak jsou, a prvky v matici B se rozmístí opět do levého a pravého sloupce.)

• Maticové násobení odpovídá skládání lineárních zobrazení, které matice reprezentují.
• Maticové násobení je distributivní vůči sčítání, tj. ${\displaystyle \mathbf {A} \cdot \left(\mathbf {B} +\mathbf {C} \right)=\mathbf {A} \cdot \mathbf {B} +\mathbf {A} \cdot \mathbf {C} }$ pro všechny matice, pro které má rovnice smysl.
• Násobení reálných resp. komplexních matic je lineární vůči násobení reálným resp. komplexním číslem, tj. ${\displaystyle \mathbf {A} \cdot \left(c\mathbf {B} \right)=(c\mathbf {A} )\cdot \mathbf {B} =c(\mathbf {A} \cdot \mathbf {B} )}$, pokud má rovnice smysl.
• Matice vzhledem k součinu můžou být dělitelé nuly, tj. součin dvou nenulových matic může být nulová matice.
• Maticové násobení není komutativní, tedy obecně ${\displaystyle \mathbf {A} \cdot \mathbf {B} \neq \mathbf {B} \cdot \mathbf {A} }$.
• Násobení matice ${\displaystyle \mathbf {A} }$ jednotkovou maticí ${\displaystyle \mathbf {E} }$ zprava i zleva je identické zobrazení, tj. ${\displaystyle \mathbf {E} \cdot \mathbf {A} =\mathbf {A} \cdot \mathbf {E} =\mathbf {A} }$, pokud má rovnice smysl.
• Maticové násobení je asociativní, tedy ${\displaystyle \mathbf {A} \cdot (\mathbf {B} \cdot \mathbf {C} )=(\mathbf {A} \cdot \mathbf {B} )\cdot \mathbf {C} }$, pokud prvky matice jsou z asociativního okruhu (např. reálná nebo komplexní čísla).
• Pro čtvercové matice platí ${\displaystyle \det(\mathbf {A} \cdot \mathbf {B} )=\det \mathbf {A} \,\det \mathbf {B} }$, tj. determinant součinu je součin determinantů.
• Transpozice součinu matic je součin transponovaných matic v opačném pořadí, tj. ${\displaystyle {(\mathbf {A} \cdot \mathbf {B} )}^{T}=\mathbf {B} ^{T}\cdot \mathbf {A} ^{T}}$
• Inverzní matice součinu regulárních matic je součin inverzních matic v opačném pořadí, tj. ${\displaystyle {(\mathbf {A} \cdot \mathbf {B} )}^{-1}=\mathbf {B} ^{-1}\cdot \mathbf {A} ^{-1}}$
• Hermitovské sdružení součinu matic je součin hermitovsky sdružených matic v opačném pořadí, tj. ${\displaystyle {(\mathbf {A} \cdot \mathbf {B} )}^{+}=\mathbf {B} ^{+}\cdot \mathbf {A} ^{+}}$

Výpočetní náročnost výše popsaného algoritmu je ${\displaystyle O(n^{3})\,\!}$ (počítáme n² čísel; pro každé potřebujeme n násobení). Existují však algoritmy s nižší složitostí vhodné pro matice vyšších řádů. Nejpoužívanější z nich je Strassenův algoritmus se složitostí ${\displaystyle O(n^{\log _{2}{7}})\approx O(n^{2.807})}$. Nižší složitost u tohoto algoritmu však získáváme za cenu snížené numerické stability. Asymptoticky nejrychlejší ze známých algoritmů je Coppersmithův-Winogradův algoritmus (${\displaystyle O(n^{2.376})\,\!}$), který je však použitelný až pro matice tak velkých řádů, že je nelze zpracovávat pomocí současných počítačů[1].

Teoreticky by se dala složitost ještě zmenšit, ale nikdy nemůže být menší než ${\displaystyle O(n^{2})\,\!}$, neboť počítáme n² čísel.

• Strassenův algoritmus
• Součin
• Skalární součin, Vnitřní součin
• Vektorový součin, Dvojitý vektorový součin
• Smíšený součin
• Tenzorový součin, Vnější součin
• Hadamardův součin
• Matice