Gradient (matematika)
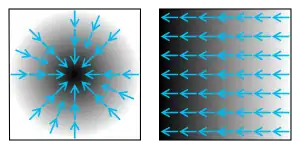
Gradient je v obecném smyslu slova směr růstu. Ve formálním jazyce matematiky označuje diferenciální operátor, jehož výsledkem je vektorové pole vyjadřující směr a velikost největší změny skalárního pole. Při formálním zápisu se používá operátor nabla .
*cos(y).png.webp)
V souřadnicovém vyjádření je v daném místě gradientem vektor, jehož složky tvoří jednotlivé parciální derivace funkce vyjadřující dané skalární pole. Pro trojrozměrné pole je gradient:
Přestože je gradient definován v kartézských souřadnicích, jde o invariantní veličinu, která nezávisí na volbě souřadnicové soustavy.
Zobecnění pro n-rozměrný prostor lze s pomocí Einsteinova sumačního pravidla vyjádřit ve tvaru
- ,
kde jsou souřadnice a jsou bázové vektory.
Operátor gradientu lze aplikovat nejen na skalární funkce, ale také na vektory a tenzory. Aplikace operátoru gradientu na tenzor zvyšuje jeho řád o jedna.
Vlastnosti gradientu
Jsou-li F,G vektorová pole, f,g funkce, a,b reálná čísla, má gradient následující vlastnosti:
Je lineární vůči reálným číslům
splňuje Leibnizovo pravidlo pro funkce
gradient skalárního součinu vektorů splňuje
Vyjádření v různých soustavách souřadnic
Následující vztahy udávají vyjádření gradientu v nejrůznějších souřadných soustavách v trojrozměrném prostoru. Je-li funkce f skalární pole v daných souřadnicích a stříškované tučné znaky souřadnic jsou jednotkové vektory báze v daných souřadnicích, pak platí
Používáme-li obecně ortogonální souřadnice x1,x2,x3, jejíž Laméovy koeficienty jsou po řadě h1,h2,h3
Ve zcela obecných souřadnicích (viz také Souřadnicový zápis vektorů) pro složky vektoru gradientu platí
Zde je potřeba podotknout, že zatímco v předchozím textu jsme za bázi brali ortonormální bázi v daných souřadnicích, ve vzorci v obecných souřadnicích používáme bázi vektorů nebo diferenciálních forem a explicitně vypisujeme jakou.
Související články
Externí odkazy
 Obrázky, zvuky či videa k tématu gradient na Wikimedia Commons
Obrázky, zvuky či videa k tématu gradient na Wikimedia Commons