Vlnky Daubechies
Daubechiesové vlnky (vlnky Daubechies) jsou rodinou ortogonálních vlnek pojmenovaných podle jejich objevitelky, belgické fyzičky a matematičky Ingrid Daubechies. Používají se při diskrétní vlnkové transformaci, nemají explicitní vyjádření a jejich konstrukce je složitá. Rodina Daubechiesové vlnek je zajímavá tím, že vlnky mají známý počet nulových momentů. Jsou konstruovány tak, že na dané délce nosiče mají právě maximální počet nulových momentů . Důsledkem toho je tato vlnka ortogonální na polynomy až do stupně (vlnková transformace bude v odpovídajících místech nulová). Tato vlastnost činí vlnky vhodnými k použití v aplikacích potlačení resp. získání polynomiální části signálu. Další aplikací je použití vlnky jako derivátoru (parciálního diferenciálního operátoru) daného řádu pro detekci nespojitostí v signálu a jeho derivacích.
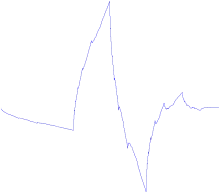
Vlnka řádu (s jedním nulovým momentem) se také nazývá Haarova vlnka.
- Vlastnosti
- asymetrické (až na )
- ortogonální, biortogonální
- délka filtrů (počet koeficientů)
- kompaktní nosič délky
- vlnky mají nulových momentů
Výpočet koeficientů
Koeficienty škálovací funkce (dolní propusti při použití ortogonální banky filtrů) musejí splňovat následující podmínky.
Normalizace:
- nebo (pak je třeba výsledné koeficienty podělit hodnotou )
z čehož plyne
- nebo (pak je třeba výsledné koeficienty podělit hodnotou )
Ortogonalita:
- pro
Nulovost momentů (uhlazenost, podmínka dolní propusti, regulárnosti):[1]
- pro
Existuje více řešení (je ovšem třeba odlišit dolní propust od horní).
Vlnky se označují jako Dx, kde x je buď počet koeficientů () nebo počet nulových momentů (), tedy např. D8 může být vlnka s 8 koeficienty (a čtyřmi nulovými momenty).
Příklad
Výpočet vlnky se 4 koeficienty (označované jako D4) v MATLABu (místo je použito pouze značení ):
t = solve(
'h0*h0 + h1*h1 + h2*h2 + h3*h3 = 1', % normalizace
'h2*h0 + h3*h1 = 0', % ortogonalita
'+(0^0)*h0 -(1^0)*h1 +(2^0)*h2 -(3^0)*h3 = 0', % nulovost nultého
'+(0^1)*h0 -(1^1)*h1 +(2^1)*h2 -(3^1)*h3 = 0' % a prvního momentu (podmínky uhlazenosti)
);
r=length(t.h0); % počet řešení
s=[1:r]; eval( [t.h0(s) t.h1(s) t.h2(s) t.h3(s)] ) % zobrazit řešení
Řešení (pouze dolní propusti):
| h0 | h1 | h2 | h3 |
|---|---|---|---|
| −0.129409522551260 | 0.224143868042014 | 0.836516303737808 | 0.482962913144534 |
| 0.482962913144534 | 0.836516303737808 | 0.224143868042014 | −0.129409522551260 |
Související články
- vlnková transformace
- kvadraturně zrcadlový filtr
- Haarova vlnka – Daubechiesové vlnka s jedním nulovým momentem
- coiflety
- symlety – rodina více symetrických vlnek se stejnými vlastnosti jako mají Daubechiesové vlnky
Reference
- ADDISON, Paul S. The Illustrated Wavelet Transform Handbook. [s.l.]: CRC Press, 2002. 353 s. Dostupné online. ISBN 0750306920, ISBN 9780750306928. Kapitola 3.5 Daubechies wavelets, s. 104. (anglicky)
Literatura
- DAUBECHIES, Ingrid. Ten Lectures on Wavelets. Philadelphia, Pennsylvania: Society for Industrial and Applied Mathematics, 1992. xix, 357 s. (CBMS-NSF regional conference series in applied mathematics; sv. 61). Dostupné online. ISBN 0898712742. (anglicky)