Definiční obor
Definiční obor funkce f[1] (nebo jen obor funkce f[2]) je množina všech hodnot, pro které je funkce definována. Definiční obor můžeme definovat pro jakékoli zobrazení. Nechť je zobrazení z množiny do množiny . Pak definiční obor zobrazení tvoří právě ty prvky množiny , pro něž je definován obraz při zobrazení . Obecně nemusí být zobrazení definováno na celé množině . V tom případě tvoří jeho definiční obor vlastní podmnožinu množiny . Občas se kromě názvu definiční obor používá také označení doména. Definiční obor zobrazení se značí většinou , či . Posledně uvedený symbol pak vychází z anglického názvu pro definiční obor (domain) a je běžně používán v cizojazyčné literatuře. V matematické notaci lze definiční obor pro zobrazení zapsat jako
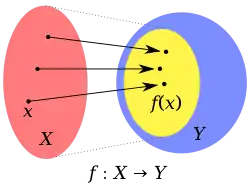
Příklad
- Funkce na množině reálných čísel není definována pro . Její definiční obor je tedy množina .
- Mezi další oblíbené příklady patří funkce složené z funkce tangens, která je definována pro všechna reálná čísla kromě lichých násobků čísla .
- Definiční obor ale nemusí tvořit jen čísla. Uvažujme například operátor derivace, který vezme funkci a vrátí její derivaci, tj. opět nějakou funkci. Neboli
kde jsme jako označili množinu reálných funkcí reálné proměnné, tj. funkcí . V tomto případě tedy tvoří definiční obor operátoru derivace ty funkce z , pro něž existuje jejich derivace. Tento příklad ukazuje zobrazení, které není definováno na celé „vstupní“ množině, protože ne všechny funkce mají derivaci.
Názvosloví
Mějme zobrazení . V závislosti na tom, zda je zobrazení definováno pro všechny prvky nebo ne, rozlišujeme následující pojmy:
- Pokud je zobrazení definováno pro všechny prvky, tak říkáme, že zobrazuje množinu do množiny .
- Pokud naopak existuje prvek z množiny , pro něž není zobrazení definováno, pak říkáme, že zobrazení zobrazuje z množiny do množiny . Občas se pro tento případ užívá značení, kdy je vstupní množina, tj. , uvedena v závorce. Neboli
Obvykle se ale za množinu bere právě definiční obor zobrazení a výše uvedenou konvenci se závorkou není třeba užívat.
Uvažujme nyní topologický prostor a na něm definované zobrazení , které zobrazuje do nějaké množiny . O zobrazení řekneme, že je hustě definované, právě když je jeho definiční obor hustou podmnožinou topologického prostoru . Neboli
kde pruh nad množinou značí uzávěr této množiny.
Omezení definičního oboru
Každou funkci (resp. obecněji zobrazení) je možno omezit na libovolnou podmnožinu jejího definičního oboru. Tedy máme-li funkci a platí-li , můžeme omezit funkci na množinu , což značíme
Takto upravená funkce pak působí na prvky z množiny stejným způsobem jako předtím na všechny prvky z množiny . Jediným rozdílem je, že už má smysl hovořit o jejích hodnotách jen na prvcích z množiny . Pro funkci se nazývá zúžení na množinu . Místo slova zúžení lze použít i cizí slovo restrikce.
Odkazy
Reference
- Přehled středoškolské matematiky, s. 130.
- Jarník Diferenciální počet I, s. 148.
Související články
Literatura
- POLÁK, Josef, 2008. Přehled středoškolské matematiky. 9. vyd. Praha: Prometheus. 659 s.
- JARNÍK, Vojtěch, 1984. Diferenciální počet (I). 7. vyd. Praha: Academia. 392 s.