Poissonovo rozdělení

Poissonovo rozdělení pravděpodobnosti popisuje náhodnou veličinu, která vyjadřuje počet výskytů jevů v určitém intervalu (času, délky, objemu), když jevy nastávají nezávisle na sobě.

Hustota pravděpodobnosti

Distribuční funkce

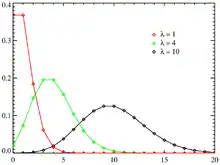
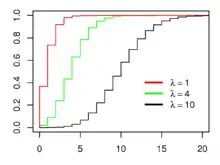
Například, občas nám přijde dopis (to je náš jev, událost). Během roku dostaneme 1460 dopisů, t.j. v průměru 4 za den. Počet příchozích dopisů během jednoho dne (to je náš časový interval) se řídí Poissonovým rozdělením. Nejvyšší je pravděpodobnost, že přijdou 4 dopisy. Pravděpodobnost dvou dopisů je o něco menší. Pravděpodobnost, že jich přijde 100, je téměř nulová.

Poissonovo rozdělení bývá označováno jako rozdělení řídkých jevů, neboť se podle něj řídí četnosti jevů, které mají velmi malou pravděpodobnost výskytu. Poissonovo rozdělení se používá k aproximaci binomického rozdělení pro velký počet pokusů, tzn. $n\to \infty$ a malou pravděpodobnost výskytu sledovaného jevu v jednom pokusu, tzn. $p\to 0$ . Obvykle můžeme binomické rozdělení aproximovat Poissonovým tehdy, pokud $n>30$ a $p\leq {\frac {1}{10}}$ . V takovém případě je $\lambda =np$ .

Rozdělení pravděpodobnosti

Poissonovo rozdělení pravděpodobnosti lze pro všechny hodnoty $x=0,1,2,...$ náhodné veličiny $X$ vyjádřit pomocí parametru $\lambda >0$ jako

P(X=x)={\frac {\lambda ^{x}}{x!}}\mathrm {e} ^{-\lambda }

pozn. e značí Eulerovo číslo

Charakteristiky rozdělení

Poissonovo rozdělení lze také popsat některými charakteristikami.

Střední hodnota Poissonova rozdělení je

\operatorname {E} (X)=\lambda

Rozptyl má hodnotu

\operatorname {D} (X)=\sigma ^{2}(X)=\lambda

Pro koeficient šikmosti dostaneme

\gamma _{1}={\frac {1}{\sqrt {\lambda }}}

Hodnota koeficientu špičatosti je

\gamma _{2}={\frac {1}{\lambda }}

Momentová vytvořující funkce Poissonova rozdělení má tvar

m(z)=\mathrm {e} ^{\lambda (\mathrm {e} ^{z}-1)}

Vícerozměrné Poissonovo rozdělení

Vícerozměrné Poissonovo rozdělení je rozdělení náhodného vektoru $X$ , jehož složky $X_{i}$ pro $i=1,2,...,n$ mají Poissonovo rozdělení s parametry $\lambda _{i}$ . Sdruženou pravděpodobnost vícerozměrného Poissonova rozdělení lze vyjádřit jako

P(x_{1},x_{2},...,x_{n})=\left\{{\begin{matrix}\mathrm {e} ^{-\sum _{i=1}^{n}\lambda _{i}}{\frac {\lambda _{1}^{x_{1}}\lambda _{2}^{x_{2}}\cdots \lambda _{n}^{x_{n}}}{x_{1}!x_{2}!\cdots x_{n}!}}&{\mbox{ pro }}x_{i}=0,1,2,...,\;\lambda _{i}>0\\0&{\mbox{ jinak }}\end{matrix}}\right.

pro $i=1,2,...,n$ .

Momentovou vytvořující funkci lze zapsat ve tvaru

m(z_{1},z_{2},...,z_{n})=\mathrm {e} ^{\sum _{i=1}^{n}\lambda _{i}\left(\mathrm {e} ^{z_{i}}-1\right)}

Příklady

Velký význam má Poissonovo rozdělení v teorii hromadné obsluhy, kde popisuje takové náhodné jevy, jako jsou příchody zákazníků.
Počet pulsů registrovaných GM-trubicí za zvolený časový interval.
Počet aut, která projedou určitým místem za daný čas.
Počet branek za fotbalový zápas.

Související články

Externí odkazy

Obrázky, zvuky či videa k tématu Poissonovo rozdělení na Wikimedia Commons
Online kalkulátor Poissonova rozdělení

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.