Navierova–Stokesova rovnice
Navierova-Stokesova rovnice je rovnice popisující proudění nestlačitelné newtonovské kapaliny. Jedná se o soustavu nelineárních parciálních diferenciálních rovnic 2. řádu. Rovnici odvodili Francouz Claude Navier a Ir George Stokes v letech 1827 a 1845 nezávisle na sobě.
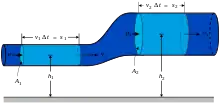
Odvození
Rovnici lze odvodit z bilance sil působících na tekutinu. Navierova-Stokesova rovnice je však speciálním případem obecné Cauchyho pohybové rovnice tekutiny, z níž lze Navierovu-Stokesovu rovnici odvodit dosazením tenzoru napětí pro newtonovskou tekutinu. Navierova-Stokesova rovnice se dá zapsat několika způsoby, například následovně
Význam jednotlivých členů:
místní zrychlení + konvektivní zrychlení = zrychlení způsobené tlakovým spádem (gradientem)+ zrychlení potřebné k překonání třecích sil + zrychlení způsobené objemovými silami
Symboly: je rychlost, je tlak, je čas, je hustota, je kinematická viskozita, je součet intenzit objemových sil (často jen tíhové zrychlení ), je operátor nabla, je symbol skalárního součinu podle konvence, že .
Řešení
Navierova-Stokesova rovnice je analyticky řešitelná jen v několika málo případech jednoduchých toků. Ve složitějších případech je nutno rovnici řešit numericky.
Nadace Clayova matematického ústavu zařadila důkaz existence hladkého řešení Navierovy-Stokesovy rovnice ve třech dimenzích na seznam sedmi nejdůležitějších matematických problémů (takzvaných Problémů tisíciletí). Na každý z nich je vypsána odměna milion dolarů.
Použití
Používá se při výpočtech proudění v aerodynamice a hydrodynamice.
Literatura
- Perry R.H.: Perry's chemical engineers' handbook, 7th edition, McGraw-Hill, New York, 1997, ISBN 0-07-049841-5
- POKORNÝ, Milan. Navier–Stokesovy rovnice [online]. [cit. 2009-11-23]. Dostupné v archivu pořízeném dne 2016-08-04. (čeština)
Související články
- Diferenciální rovnice
- Mechanika tekutin
- Pohybová rovnice tekutiny
- Rovnice kontinuity
Externí odkazy
 Obrázky, zvuky či videa k tématu Navierova-Stokesova rovnice na Wikimedia Commons
Obrázky, zvuky či videa k tématu Navierova-Stokesova rovnice na Wikimedia Commons