Konceptuální graf

Na model jsou kladeny následující požadavky:

1. Intuitivnost (orig. familiar conventions) – Běžný uživatel by měl být schopen pokládat systému dotazy aniž by se musel zaobírat technickými detaily systému.
2. Automatická inference – Systém je schopný odvozovat vztahy, které v něm nejsou explicitně zabudované.
3. Přirozenost – Formalizmus zápisu vztahů by měl být podobný sémantice přirozeného jazyka.
4. Sémantická integrita – Omezení datové domény by měla pomoci udržet databázi v takovém stavu, aby co nejlépe odrážela realitu.

(Sowa, "Conceptual Graphs for a Data Base Interface", 1976)

Z pohledu zápisu je konceptuální graf neorientovaným souvislým konečným bipartitním grafem. Jeho bipartita vypadá tak, že v jedné množině vrcholů bipartitního grafu jsou koncepty, v druhé vztahy. Lidově řečeno, v konceptuálním grafu lze hranou spojit vždy jen koncept se vztahem, ale nikoli dva vztahy nebo dva koncepty navzájem.

Základním stavebním kamenem je koncept, který se značí obdélníkem s názvem typu konceptu (v originále "sort label"). Koncept je pouze jakýsi obecný objekt, který může reprezentovat cokoli chceme, např. ČÍSLO, ČLOVĚK nebo ÚČET jsou koncepty. Pokud bychom si chtěli koncept nějak přiblížit, dá se říci že je to analogie datových typů které se vyskytují v programovacích jazycích, obecněji, že jde o entity. Dalším kamenem jsou konceptuální vztahy, jinak též nazývané relace. Konceptuální vztahy se zapisují do kroužků. Ke každému konceptuálnímu vztahu existuje alespoň jedna hrana v grafu (tzv. link), která ho spojuje s nějakým konceptem. Jednoduchý konceptuální graf můžeme vidět na následujícím obrázku.

Příklad jednoduchého konceptuálního grafu.

Tento konceptuální graf vyjadřuje fakt, že "chlapec jde". Obsahuje dva koncepty – "chlapec" a "chůze" a vztah "agent", který říká že chlapec je entitou, která provozuje nějakou činnost (chůzi). Tento obrázek je klasickým příkladem tzv. dyadického vztahu (vztahu přesně dvou entit). Podle počtu linků mezi vztahem a na něj vázanými koncepty potom mluvíme o vztazích ternárních (triadických), kvaternárních, … a obecně tedy n-árních.

V realitě se objevují koncepty, které mají různou úroveň obecnosti a jejichž konkrétní prvky mohou být vzájemnými podmnožinami. Například ZVÍŘE je podtypem ŽIVOČICH. Tomuto vztahu se říká podtyp a vyjadřuje vzájemnou povahu konkrétních prvků určitých typů konceptů. Samotný konstrukt konceptu není ale ovlivněn – každý typ konceptu je jedinečný i přesto, že oba mohou reprezentovat stejná data. Na množině všech typů konceptů definujeme částečné uspořádání za pomoci operátoru ≤ tak, jak je pro částečné uspořádání zvykem.

Dva koncepty mohou mít jeden nebo více společných podtypů (angl. common subsort). Například pokub bychom měli koncepty CELÉ-ČÍSLO a KLADNÉ-ČÍSLO jejich společným podtypem bude CELÉ-KLADNÉ-ČÍSLO. Je vidět, že ačkoliv CELÉ-ČÍSLO i KLADNÉ-ČÍSLO jsou koncepty existující samy o sobě, jejich "sloučením" dostaneme nový, úžeji specifikovaný koncept. Tento koncept lze formálně definovat s použitím relace částečného uspořádání takto:

Společný podtyp

Společným podtypem (common subsort) konceptů a a b je koncept c, právě tehdy pokud platí typ(c) ≤ typ(a) a zároveň typ(c) ≤ typ(b). Funkce typ vyjadřuje typ (orig. sort label) daného konkrétního konceptu.

Pomocí konceptů a vztahů modelujeme základní sémantiku naší problémové domény. Pro tvorbu konceptuálních grafů platí sada pravidel, jejichž dodržení má za následek vznik validního (tzv. well-formed) grafu. Rozšiřování či zmenšování existujícího konceptuálního grafu podle těchto pravidel nemůže jeho validitu poškodit. Pravidla pro tvorbu CG jsou následující:

Definice

Za předpokladu, že máme množinu well-formed konceptálních grafů, získáme z nich well-formed koncetpuální graf(y) opakovanou aplikací těchto kroků. Graf skládající se z jednoho osamoceného kontextu je validní (well-formed).

1. Kopírování – Identická kopie validního konceptuálního grafu je taktéž validní konceptuální graf.
2. Oddělení – Všechny souvislé grafy, které jsou výsledkem vymazání konceptuálního vztahu (relace) z grafu, jsou validní. Tedy: smažeme-li z grafu uzel vztahu, graf se nám sice může rozpadnout na více samostatných souvislých grafů, ale z pohledu validity CG nic tím nerozbijeme.
3. Restrikce – Nahradíme-li v grafu konkrétní typ konceptu jeho podtypem, konceptuální graf zůstane validní.
4. Spojení – Mějme dva různé konceptuální grafy, přičemž v obou se vyskytuje stejný typ konceptu. Tyto grafy můžeme sloučit tak, že z jednoho daný uzel typz konceptu smažeme a všechny hrany, které do něj vedly, napojíme na stejný typ konceptu v druhém grafu. Výsledkem je sloučený graf, který je opět validní.

Pravidlo restrikce aplikované na koncept ČLOVĚK.

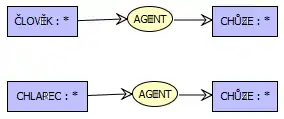
Obrázek ukazuje princip restrikce. Z původního konceptuálního grafu, který vyjadřoval fakt "člověk jde" jsme vytvořili "chlapec jde" pomocí restrikce typu ČLOVĚK na typ CHLAPEC. Protože CHLAPEC ≤ ČLOVĚK, validita grafu je zachována.

Pravidlo spojení aplikované na dva konceptuální grafy. SPojení je provedené na konceptu CHŮZE.

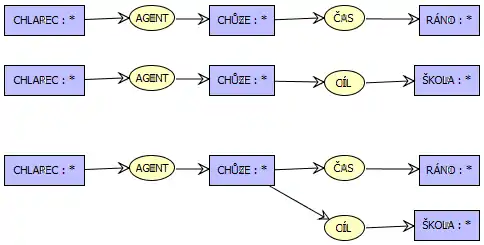
Obrázek zachycuje princip spojení. Původní konceptuální grafy vyjadřující fakty "chlapec jde ráno" a "chlapec jde do školy" jsme sloučili nad konceptem CHŮZE a dostali jsme fakt "chlapec jde ráno do školy".

Pravidlo oddělení aplikované na relaci ČAS.

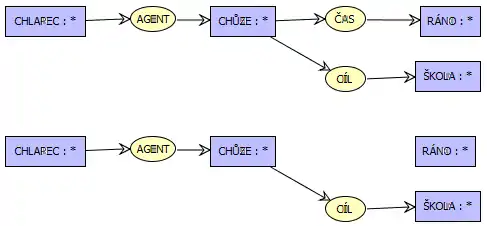
Obrázek zachycuje princip oddělení. Původní konceptuální graf vyjadřující "chlapec jde ráno do školy" jsme roztrhli odebráním vztahu ČAS. Výsledný graf vyjadřuje fakt "chlapec jde do školy", přičemž koncept RÁNO je samostatný a informaci o chlapci jdoucím do školy již nijak neovlivňuje.

Protože konceptuální grafy podporují automatickou inferenci (odvozování závěrů z předpokladů), z výše zmíněných základních pravidel mohou automaticky vznikat pravidla další. Mezi nejvýznamnější patří projekce, která má nezastupitelné místo v prostředí relačních databází. V řeči CG je výsledkem projekce dvou konceptuálních grafů na sebe jejich největší společný podgraf, přičemž v úvaze musíme vzít i podtypy jednotlivých konceptů.

Projekce dvou konceptuálních grafů a její výsledek (dole).

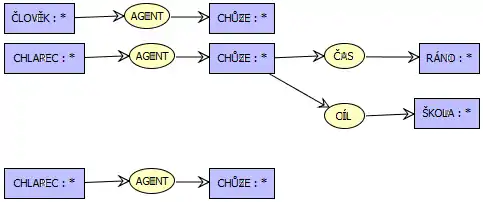
Na obrázku vidíme projekci dvou konceptuálních grafů (fakty "člověk jde" a "chlapec jde ráno do školy"), jejichž výsledkem je největší společný podgraf, který vyjadřuje fakt "chlapec jde".

V konceptuálních grafech se vyskytují nejen obecné koncepty, ale i koncepty s konkrétní hodnotou nebo s kvantifikátorem. Tyto informace se zapisují jako TYP-KONCEPTU: REFERENT. V případě obecných (angl. indefinite) konceptů pak najdeme například CHLAPEC: * což je formálně správným vyjádřením konceptu "(nějaký) chlapec". Pokud bychom ovšem do konceptu napsali konkrétní hodnotu (konstantní koncept), například CHLAPEC: Pavel, už jsme vytvořili chlapce Pavla. Konkrétní konstantě (v tomto případě "Pavel") se také říká designátor. Zapisovat můžeme i množinu hodnot, např. CHLAPEC: {Petr, Pavel}. Pokud bychom použili třeba obecný kvantifikátor, koncept (kvantifikovaný koncept) by vypadal CHLAPEC: ∀ a reprezentoval by fakt "všichni chlapci". Dalším povoleným kvantifikátorem je kvantifikátor existenční. V analogii na programovací jazyk, koncepty si můžeme představit jako datové typy a nyní řešíme, jakou mohou skutečně nabývat hodnotu, přičemž již máme (díky konstruktu podtypů) i hierarchii nadtyp-podtyp. Poslední možností reprezentace hodnoty je tzv. deskriptor. V sekci o vnořených modelech je vysvětleno, že konceptuální grafy lze do sebe vnořovat. Deskriptor je konceptuální graf, který vysvětluje daný koncept.

Lambda výrazy nám umožňují definovat složitější vztahy libovolné arity. Lambda výraz je šablonou (makrem), ze které se po dosazení proměnných stává konkrétní fakt.

Příklad lambda výrazu, který tvoří unární relaci.

Takovýto lambda výraz můžeme číst jako "chlapec λ₁ jde" a sám o sobě nemá žádný pořádný význam. Teprve pokud dosadíme λ₁ = Pavel, obdržíme fakt "chlapec Pavel jde". Námi vytvořený lambda výraz je unární relací, protože obsahuje pouze jednu volnou proměnnou. Kdybychom ještě nahradili CHŮZE: * za CHŮZE: λ₂, dostali bychom relaci binární. Ta by nám například pak umožňovala vytvářet fakty jako "chlapec Pavel jde pomalu" pro λ₁ = Pavel a λ₂ = pomalá.

Konceptální grafy jsou poměrně lehce převoditelné do predikátové logiky. Například fakt vyjádřený konceptem CHLAPEC: Pavel bychom převedli následovně:

∃x Chlapec(x) ∧ Jméno(x,Pavel)

Každou relaci (konceptuální vztah) pak převádíme jako n-ární predikát.

V predikátové logice má každá logická proměnná svoje označení. Pokud spojujeme dvě nebo více tvrzení predikátové logiky, nevyhneme se přeznačování logických proměnných. To u konceptuálních grafů odpadá, protože logické proměnné mají pouze svou grafickou podobu (obdélníček s konceptem), nikoli přiřazené formální označení – to v predikátové logice slouží stejně jen k tomu, abychom věděli, o které proměnné je zrovna řeč. Sowa ve svém základním textu zmiňuje následující jev:

∀x ∀y ∃z (z=rozdíl(x,y))

Formule predikátové logiky nám říká, že pro každá dvě čísla x,y existuje číslo z, které je jejich rozdílem. Ve formě konceptuálního grafu tento fakt vypadá následovně:

Příklad zobrazení funkčních závislostí v konceptuálním grafu.

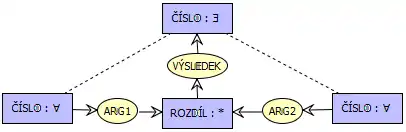
Na obrázku jsou nejzajímavější přerušované čáry vedoucí mezi obecnými a existenšním kvantifikátorem. Tyto čáry vyjadřují závislost existenčního kvantifikátoru na kvantifikátorech obecných a přirozeně tedy formují vztahy reprezentované ve formuli predikátové logiky. Takovýmto závislostem se říká funkční závislosti. Funkční závislosti jsou ovšem mnohem mocnější. Představme si predikát P(x,y,z,w), kde x a y jsou kvantifikovány obecným kvantifikátorem a z a w kvantifikátorem existenčním, přičemž z závisí pouze na x a w závisí pouze na y. Formule predikátoé logiky vypadají následovně:

∀x ∃z ∀y ∃w (P(x,y,z,w))
∀y ∃w ∀x ∃z (P(x,y,z,w))

Je vidět, že v každé z uvedených formulí jsou dvě logické proměnné uvedeny naprosto zbytečně. Kdybychom tento fakt zachytili pomocí konceptuálního grafu, bude nám stačit zachytit pouze existující funkční závislosti x -> z a y -> w aniž bychom museli používat nadbytečné konstrukty.

Funkční závislost

Funkční závislost v konceptuálním grafu je množina funkčních hran (angl. function links) vedoucích z tzv. zdrojového konceptu (konceptů) do tzv. cílového konceptu (konceptů). S každou funkční závislostí se pojí tzv. přístupová funkce (angl. access procedure). Kdykoliv známe všechny hodnoty zdrojových konceptů, přístupová procedura je schopná dopočítat hodnoty cílových konceptů.

Funkční závislosti – a přístupové procedury – jsou klíčovým prvkem pro přechod od konceptuálních grafů k fyzickému hledání dat v databázovém systému. Představme si následující SQL dotaz:

select jméno, příjmení, mzda, nadřízený from zaměstnanci where oddělení = 'personální'.

Výsledkem dotazu bude výpis zaměstnanců pracujících v personálním oddělení – jejich jména a příjmení, mzdy a jejich nadřízeného. Z pohldeu funkčních závislostí v konceptuálním grafu je ODDĚLENÍ zdrojovým konceptem, koncepty JMÉNO, PŘÍJMENÍ, MZDA a NADŘÍZENÝ cílovými koncepty funkčních závislostí. Přístupová procedura pak definuje konkrétní algoritmus pro nalezení požadovaných dat.

Každý z konceptuálních grafů může být součástí většího konceptuálního grafu. Takovýto vnořený graf (angl. nested graph) se zobrazuje jako jeden koncept. Za konceptem se potom skrývá zmíněný graf. Odkazy (např. funkční závislosti) pak mohou směřovat do konkrétních uzlů takto vnořených grafů. Vnořené grafy jsou velmi důležité, protože nám umožňují definovat kontext jednotlivých znalostí. Následující konceptuální graf reprezentuje znalost, že "John říká, že všichni psi jsou chytří."

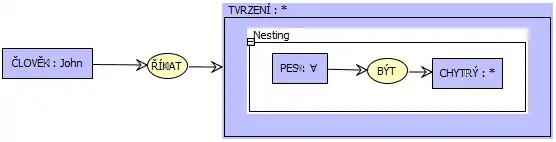
Jednoduchý příklad vnořeného konceptuálního grafu, který udává kontext daného faktu. Inspirováno: P. Křemen, https://cw.fel.cvut.cz/wiki/_media/courses/a7b33sui/01-cg.pdf .

Konceptální schémata jsou konceptuálním grafem, ve kterém se vyskytují určité kombinace kvantifikátorů a funkčních závislostí. Funkční závislosti v konceptuálním schématu totiž formují strukturu, která poskytuje přímé mapování na databázové úložiště. Při zodpovídání užvatelského dotazu se systém snaží převést podobu v (přibližně) přirozeném jazyce právě na konceptuální schéma.

Vrátíme se o kousek zpět k proměnným a kvantifikátorům v konceptuálním grafu a nejdříve doplníme jejich formální definici:

Definice

Pro formální definici se používají dva selektory nazývané value a quant (česky bychom řekli asi "hodnota" a "množství", raději ale ponecháme názvy v původní podobě). Předpokládejme, že tyto funkce mohou být aplikovány na jakýkoliv koncept. Funkce mají následující vlastnosti (pro nějaký koncept c).

1. Pokud jsou value(c) i quant(c) nedefinovány, c je obecný koncept.
2. Pokud je value(c) definována a quant(c) nedefinována, c je konstantní koncept.
3. Pokud je value(c) nedefinována a quant(c) definována, c je kvantifikovaný koncept.
4. Nemůže nastat situace, kdy jsou zároveň value(c) i quant(c) definovány.
5. Pokud je quant(c) definována, nabývá jedné z hodnot {∀,∃,E,E-set}. E značí výskyt přesně jedné hodnoty (odpovídá někdy používanému matematickému značení ∃!) a E-set značí množinu přesně daných hodnot. Pro tyto kvantifikátory platí slabší podmínka – že daná množina může být i prázdná.
6. Existuje funkce permissible, která definuje množinu povolených hodnot pro daný koncept. Formálně: pro každý konstantní koncept c platí value(c) ∈ permissible(typ(c)).
7. Funkce permissible respektují vytah nadtyp-podtyp daných konceptů. Tedy pokud máme dva konstantní koncepty a jeden je podtypem druhého, pak jeho množina povolených hodnot je podmnožinou povolených hodnot jeho nadtypu.

(Sowa, "Conceptual Graphs for a Data Base Interface", 1976)

Konceptuální schéma

Konceptuální schéma je validní konceptuální graf, který má alespoň jednu funkční závislost. Koncept může být zdrojem libovolného počtu funkčních závislostí, ale žádný koncept nemůže být cílem více než jedné funkční závislosti.

• Pokud je koncept c zdrojem, ale není cílem funkční závislosti, pak quant(c) = ∀.
• Pokud je koncept c zdrojem i cílem funkční závislosti, pak quant(c) = E.
• Pokud je koncept c pouze cílem funkční závislosti, pak quant(c) ∈ {E,E-set}.
• Pokud koncept není ani zdrojem ani cílem funkční závislosti, pak je obecným konceptem.

(Sowa, "Conceptual Graphs for a Data Base Interface", 1976)

Pokud bychom měli databázi o několika tabulkách se vzájemnými vazbami, tato databáze je provázána konstrukty, kterým se říká cizí klíče. Databázová tabulka, která se neodkazuje na žádnou jinou je obecně kvantifikovaným konceptem. Konceptuální vztahy popisují chápání a významové vazby dat. Funkční závislosti reprezentují fyzickou přítomnost konstruktů cizích klíčů v databázovém schématu.

Výše popsaný model konceptuálních grafů umožňuje na rozdíl od predikátové logiky prvního řádu vytvářet nerozhodnutelná schémata. Problém je v příliš expresivním množinovém designátoru a v deskriptorech. John Sowa tento problém řešil pomocí tzv. simple conceptual graphs, které použití těchto dvou prvků zapovídají (Sowa 1984). Myšlenku "simple graphs" dále rozpracovali Michel Chein a Marie-Laure Mugnier v roce 1992[1].

Za účelem lepší reprezentace libovolného jazyka či logiky se postupně vyvíjely rozšiřující modely. Tato rozšíření lze klasifikovat do několika stupňů[2]:

• Core CGs: Beztypová logika pokrývající "Comon Logic" standardizovanou prostřednictvím ISO/IEC 24707.
• Extended CGs: Přidává do konceptuálních grafů některé další prvky (univerzální kvantifikátor, typová návěstí a Boolovské kontexty). Jde o rozšíření za účelem efektivnějšího zápisu, vyjadřovací síla obou variant (Core i Extended) je stejná a existuje algoritmus na vzájemný převod těchto dvou variant.
• CGs with contexts: Umožňuje podporu meta-jazyků (jazyků popisujících jiné jazyky). Kontexty zde realizují chybějící potřebu odvozovat tvrzení o objektech z tvrzení o meta-objektech.
• Research CGs: Různé variace a odnože konceptuálních grafů, které jsou aktivně ve vývoji. Úspěšná rozšíření tohoto typu mohou být později začleněna do standardu.

První z vývojových větví je vývoj rozhraní pro grafickou tvorbu výroků predikátové logiky. V takovém přístupu, je vzorec v predikátové logice (prvního řádu) vyjádřen pojmenovaným grafem. Má lineární notaci. Formát pro výměnu konceptuálních grafů (Conceptual Graph Interchange Format (CGIF) byl standardizován normou ISO/IEC 24707:2007 pod ISO jako jeden ze tří dialektů „Obecné logiky“ Common Logic, která tvoří rámec skupiny jazyků založených na logice.

Kočka Elsie sedí na rohožce

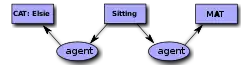
Uvedený diagram je příkladem způsobu zobrazení konceptuálního grafu. Obdélníky tvoří pojmové (konceptuální) uzly a ovály zobrazují „vztahové“ uzly. Ve výše zmíněném zápisu (CGIF) by byl tento konceptuální graf zapsán následovně:

   [Cat Elsie] [Sitting *x] [Mat *y] (agent ?x Elsie) (location ?x ?y)

V hranatých závorkách jsou uzavřeny informace z uzlů konceptů a do kulatých závorek se zapisují vztahové uzly. Písmena x a y se nazývají „koreferenční štítky,“ které značí, jakým způsobem jsou konceptuální a vztahový uzel vzájemně propojeny.

Ve formátu Common Logic Interchange Format (CLIF) jsou tato písmena namapována na proměnné, viz následující příklad:

   (exists ((x Sitting) (y Mat)) (and (Cat Elsie) (agent x Elsie) (location x y)))

Srovnáme-li oba zápisy, tak jak ukazuje první příklad (ve zápis ve formátu CGIF), hvězdičky u koreferenčních štítků *x a *y odpovídají (v zápise formátu CLIF) existenčním kvantifikátorům proměnných. A dále otazníkům z prvního zápisu odpovídají vázaným proměnným druhého zápisu. Univerzální kvantifikátor by se v CGIF zapsal @every*z a v CLIF forall (z).

Prověření syntaxe může být provedeno tak, že přepíšeme graf do logického zápisu a takový zápis necháme přeložit robotem.

Druhá vývojová větev je vystavěna na základech existenčních grafů navržených Charlesem Sandersem Peircem, které spadají do původních grafů navržených Johnem Sowou. V tomto přístupu, který vyvíjel převážně Frithjof Dau, jsou konceptuální grafy spíše (podle definice teorie grafů) konceptuálními diagramy, než grafy. Prověřovací operace jsou prováděné v těchto diagramech.

Třetí větví vývoje konceptuálních grafů tvoří reprezentace znalostí pomocí grafů a logický ověřovací aparát (GBKR). Tento přístup vyvinuli Michel Chein a Marie-Laure Mugnier. Hlavními znaky jsou:

• všechny druhy znalostí (ontologie, pravidla, omezení a fakta) jsou označené grafy, které poskytují intuitivní a snadné pochopení významu reprezentovaných znalostí
• ověřovací mechanismy jsou založené na zápisu grafu, především na klasickém zápisu grafového homomorfismu (mapování dvou grafů na sebe s respektováním jejich struktury), což umožní především napojit základní ověřované problémy na jiné fundamentální problémy v počítačové vědě
• forma je vystavěná na logice, tzn. má sémantiku logiky prvního řádu a vyvozovací mechanismus je jednoznačný a úplný s ohledem na dedukci v logice prvního řádu
• z hlediska výpočetního, byl homomorfismus grafů přijat v 90. letech jako hlavní používaný zápis a výpočet komplexity a algoritmická účinnost našly uplatnění v několika málo oblastech

V tomto článku byl použit překlad textu z článku Conceptual graph na anglické Wikipedii.

SOWA, John F. Conceptual Graphs for a Data Base Interface [online]. 1976. Dostupné online. (anglicky)

• Chein, Michel; Mugnier, Marie-Laure (2009). Graph-based Knowledge Representation: Computational Foundations of Conceptual Graphs. Springer. ISBN 978-1-84800-285-2.
• Dau, F. (2003). "The Logic System of Concept Graphs with Negation and Its Relationship to Predicate Logic". Lecture Notes in Computer Science (Springer) 2892.
• Harmelen, Frank van; Lifschitz, Vladimir; Porter, Bruce. (December 2007). Handbook of Knowledge Representation. Elsevier. ISBN 978-0-444-52211-5. 213-237.
• Křemen, Petr. "Konceptuální grafy". Přednáška - Katedra kybernetiky, FEL ČVUT v Praze
• Sowa, John F. (July 1976). "Conceptual Graphs for a Data Base Interface". John F. Sowa personal page 20 (4): 336–357.
• Sowa, John F. (1984). Conceptual Structures: Information Processing in Mind and Machine. Reading, MA: Addison-Wesley. ISBN 978-0-201-14472-7.
• Galitsky, Boris; Dobrocsi, Gabor; de la Rosa, Josep Lluis; Kuznetsov, Sergei O. (2010). "From Generalization of Syntactic Parse Trees to Conceptual Graphs". Lecture Notes in Computer Science (Springer) 6208.

• Resource Description Framework
• Reprezentace znalostí
• Sémantický web
• Ontologie (informatika)
• Mikroformát
• Sémantika

• Conceptual Structures Home Page. Old site: Conceptual Graphs Home Page. Yearly international conferences (ICCS): list; also see Uta Priss's table and Arisbe's list Archivováno 29. 8. 2013 na Wayback Machine (with Wayback Machine links).
• Graph-Based Knowledge Representation (book)
• John F. Sowa - Conceptual Graphs
• Sowa, John F.. "Laws, Facts, and Contexts: Foundations for Multimodal Reasoning".
• University of Aalborg Online Course
• CoGui
• Cogitant
• Přednáška Ing. Petra Křemena z Katedry kybernetiky FEL ČVUT