Cykloida

Prostá cykloida

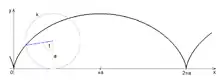
Pokud bod pevně spojený s kružnicí leží na jejím obvodu, pak při valení této kružnice po přímce opisuje tento bod prostou (obecnou, obyčejnou) cykloidu.

Prostou cykloidu lze vyjádřit parametricky:

${\displaystyle x=a(t-\sin t)}$,

${\displaystyle y=a(1-\cos t)}$,

kde ${\displaystyle a}$ je poloměr kružnice a parametr ${\displaystyle t}$ je úhel otočení kutálející se kružnice.

První, resp. druhou polovinu prvního oblouku prosté cykloidy lze vyjádřit v explicitním tvaru

${\displaystyle x=a\arccos {\frac {a-y}{a}}-{\sqrt {y(2a-y)}}}$

pro ${\displaystyle x\in \langle 0,\pi a\rangle }$, resp.

${\displaystyle x=a\left(2\pi -\arccos {\frac {a-y}{a}}\right)+{\sqrt {y(2a-y)}}}$

pro ${\displaystyle x\in \langle \pi a,2\pi a\rangle }$.

Perioda cykloidy je ${\displaystyle 2\pi a}$.

Délka oblouku dané větve prosté cykloidy od hrotu do bodu ${\displaystyle [x(t),y(t)]}$ pro ${\displaystyle t\in \langle 0,2\pi \rangle }$ je

${\displaystyle s=4a\left(1-\cos {\frac {t}{2}}\right)}$.

Dosazením periody získáme pro délku jedné větve prosté cykloidy výraz

${\displaystyle s=8a}$.

Obsah plochy ohraničené jednou větví prosté cykloidy je

${\displaystyle S=3\pi a^{2}}$.

Poloměr křivosti v bodě různém od hrotu prosté cykloidy je

${\displaystyle R=4a\left|\sin {\frac {t}{2}}\right|}$,

takže poloměr křivosti ve vrcholu je maximální:

${\displaystyle R=4a}$.

Nejjednodušší přirozená rovnice prosté cykloidy je

${\displaystyle R^{2}+s^{2}=16a^{2},s\in \langle -4a,+4a\rangle ,}$

kde však oblouk ${\displaystyle s}$ počítáme od vrcholu.

Evolutou cykloidy je shodná cykloida, která je ve směru osy ${\displaystyle x}$ posunuta o ${\displaystyle \pi a}$ souhlasně s původní cykloidou a ve směru osy ${\displaystyle y}$ je posunuta o ${\displaystyle 2a}$ nesouhlasně s orientací původní cykloidy.

Zkrácená cykloida

Prodloužená cykloida

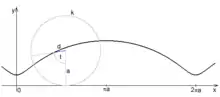
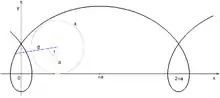
Pokud bod pevně spojený s kutálející se kružnicí neleží na obvodu této kružnice, ale jeho vzdálenost od středu kružnice o poloměru ${\displaystyle a}$ je ${\displaystyle d}$, pak pro ${\displaystyle d<a}$ získáme cykloidu zkrácenou a pro ${\displaystyle d>a}$ cykloidu prodlouženou.

Parametrické rovnice zkrácené, resp. prodloužené cykloidy lze zapsat ve tvaru

${\displaystyle x=at-d\sin t}$

${\displaystyle y=a-d\cos t}$

• Prostá cykloida má nekonečně mnoho hrotů.
• Všechny prosté cykloidy mají stejný tvar, jsou podobné.
• Zkrácená cykloida má nekonečně mnoho inflexních bodů.
• Prodloužená cykloida má nekonečně mnoho uzlů (dvojných bodů).
• Oblouk cykloidy snese ze všech oblouků největší zatížení, proto mnoho oblouků mostů má právě její tvar.
• Část cykloidy je řešením úlohy o brachistochroně

• Cyklická křivka
• Brachistochrona

• Obrázky, zvuky či videa k tématu Cykloida na Wikimedia Commons
• Jak vyrobit brachistochronu (video)
• Cykloidy v Cabri
• Cyklické pohyby (teorie, obrázky v Gnuplotu)