Povrch s nulovou rýchlosťou
Povrch s nulovou rýchlosťou alebo povrch nulovej rýchlosti je koncept, ktorý sa týka gravitačného problému n-telies. Predstavuje hraničný povrch, ktorý teleso s danou energiou nemôže prekročiť, pretože má na ňom nulovú rýchlosť. Prvýkrát ho predstavil George William Hill.[1] Povrch s nulovou rýchlosťou je obzvlášť významný pri práci so slabými gravitačnými interakciami medzi obiehajúcimi telesami.
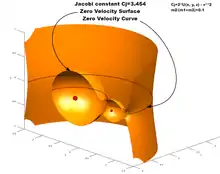
Problém troch telies
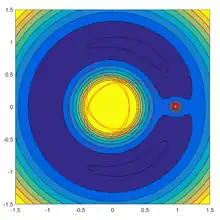
Pri kruhovo obmedzenom probléme troch telies obiehajú dve ťažké telesá v konštantnej radiálnej vzdialenosti, konštantnou uhlovou rýchlosťou a teleso zanedbateľnej hmotnosti je ovplyvnené ich gravitáciou. V rotačnom súradnicovom systéme, v ktorom sú telesá nehybné, sa zavedie odstredivá sila. V tomto súradnicovom systéme energia a hybnosť nie sú oddelene a Jacobi integrál je konštantný:
kde je rýchlosť rotácie, umiestnenie častice v rotujúcom súradnicovom systéme, – vzdialenosti k telesám a – ich hmotnosti krát gravitačná konštanta.[2]
Pre danú hodnotu , body na povrchu
vyžadujú, aby . To znamená, že častica nebude schopná prejsť cez tento povrch. Toto je povrch s nulovou rýchlosťou.[3]
Všimnite si, že nulová rýchlosť je v rotujúcom rámci, v neotáčajúcom rámci častice rotujú s ostatnými telesami. Povrch tiež predpovedá len to, do ktorých oblastí nie je možné vstúpiť, nie tvar trajektórie vnútri povrchu.[2]
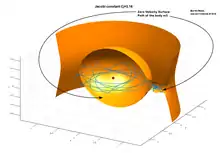
Zovšeobecnenie
Túto koncepciu možno zovšeobecniť na zložitejšie problémy, napríklad na telesá na eliptických obežných dráhach,[4] všeobecný rovinný problém s tromi telesami,[5] problém so štyrmi telesami so slnečným vetrom[6] alebo v prstencoch.[7]
Lagrangeove body
Povrch s nulovou rýchlosťou je tiež dôležitým parametrom pri hľadaní Lagrangeových bodov. Tieto body zodpovedajú miestam, kde má efektívny potenciál rotujúceho súradnicového systému extrémny. To zodpovedá miestam, kde sa povrchy s nulovou rýchlosťou zachytia a ak sa zmení vytvárajú otvory.[8] Pretože trajektórie sú ohraničené povrchmi, trajektória, ktorá sa snaží uniknúť (alebo vstúpiť) do oblasti s minimálnou energiou, bude typicky prechádzať blízko Lagrangeovho bodu, ktorý sa používa pri plánovaní nízko energetickej trajektórie.
Zhluky galaxií
Vzhľadom na skupinu galaxií, ktoré gravitačne intereagujú, sa povrch nulovej rýchlosti používa na určenie toho, ktoré objekty sú gravitačne viazané (tj. nie sú prekonané Hubblovou expanziou), a teda sú súčasťou klastra galaxií, ako je napríklad miestna skupina.[9]
Pozri aj
- Hillova sféra
- Nízko energetický transfer
- Orbitálna mechanika
Referencie
- G. W. Hill, Researches in the lunar theory. Am. J. Math. 1, 5, (1878) p. 129. https://www.jstor.org/stable/2369430?seq=1#page_scan_tab_contents
- SCHAUB, Hanspeter; JUNKINS, John L.. Analytical Mechanics of Space Systems, Fourth Edition. Washington, DC : American Institute of Aeronautics and Astronautics, Inc., 2018-01-19. Dostupné online. ISBN 978-1-62410-521-0. DOI:10.2514/4.105210 (po anglicky)
- Zero-Velocity Surfaces [online]. farside.ph.utexas.edu, [cit. 2020-01-03]. Dostupné online.
- Szenkovits, Z. M. F., & Csillik, I. (2004). Polynomial representation of the zero velocity surfaces in the spatial elliptic restricted three-body problem. Pure Mathematics and Application, 15(2-3), 323-322.
- Bozis, G. (1976). Zero velocity surfaces for the general planar three-body problem. Astrophysics and Space Science, 43(2), 355-368.
- Kumari, R., & Kushvah, B. S. (2013). Equilibrium points and zero velocity surfaces in the restricted four-body problem with solar wind drag. Astrophysics and Space Science, 344(2), 347-359.
- Kalvouridis, T. J. (2001). Zero-velocity surfaces in the three-dimensional ring problem of N+ 1 bodies. Celestial Mechanics and Dynamical Astronomy, 80(2), 133-144.
- CRTBP Pseudo-Potential and Lagrange Points [online]. LagrangePointsPub.m, 2013-10-13, [cit. 2020-01-03]. Dostupné online.
- Galaxies and the Universe – Galaxy Groups and Clusters [online]. pages.astronomy.ua.edu, [cit. 2020-01-03]. Dostupné online.
Zdroj
Tento článok je čiastočný alebo úplný preklad článku Zero-velocity surface na anglickej Wikipédii.