Efektívny potenciál

Efektívny potenciál (alebo aj účinný potenciál) kombinuje potenciálnu energiu a tangenciálnu kinetickú energiu obiehajúceho objektu.[1] Efektívny potenciál napriek svojmu názvu nie je v skutočnosti potenciál, ale má rozmer energie. Môže sa použiť na určenie orbity planét. Základná formulácia efektívneho potenciálu je:[2]

Efektívny potenciál. E>0 hyperbola, E=0 parabola, E<0 elipsa. Body A1,...,A4 sa nazývajú body obratu.

${\displaystyle U_{\text{eff}}(\mathbf {r} )={\frac {L^{2}}{2\mu r^{2}}}+U(\mathbf {r} )}$

• L je moment hybnosti
• r je vzdialenosť medzi dvoma telesami
• μ je redukovaná hmotnosť telies (μ=m1m2/(m1+m2))
• U (r) je gravitačná potenciálna energia

Efektívnou silou (účinnou silou) je potom negatívny gradient efektívneho potenciálu:

${\displaystyle {\begin{aligned}\mathbf {F} _{\text{eff}}&=-\nabla U_{\text{eff}}(\mathbf {r} )\\&={\frac {L^{2}}{\mu r^{3}}}{\hat {\mathbf {r} }}-\nabla U(\mathbf {r} )\end{aligned}}}$

Vizualizácia efektívneho potenciálu kruhovo obmedzeného problému troch telies (Ueff červený model s bielymi čiarami ekvipotenciálu), Libračné body (modré v rovine obežnej dráhy a čierna ich projekcia na Ueff) a planéta obiehajúcu hviezdu (červené body v mierke ich hmotnosti 0,01)

V klasickej, nerelativistickej Newtonovskej fyzike je efektívny potenciál:[3]

${\displaystyle U_{\text{eff}}(r)={\frac {L^{2}}{2mr^{2}}}-{\frac {GmM}{r}}}$

${\displaystyle L=mr^{2}{\omega }\,}$

• m, M - hmotnosť obiehajúceho a centrálneho telesa
• G - gravitačná konštanta
• ω - uhlová rýchlosť

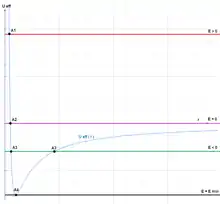
Podľa grafu Ueff možno opísať pohyb telesa v centrálnom poli v závislosti od hodnoty celkovej mechanickej energie:[4]

1. E>0 - teleso sa pohybuje po hyperbole a bod A₁ zodpovedá pericentru jeho trajektórie;

2. E=0 parabola - teleso sa pohybuje po parabole a bod A₂ zodpovedá pericentru jeho trajektórie;

3. E<0 - teleso sa pohybuje po elipse, pričom bod A₃ zodpovedá pericentru bod A'₃ apocentru jeho trajektórie;

4. E=E_min- teleso má najmenšiu možnú zápornú celkovú mechanickú energiu a pohybuje sa po kružnici s polomerom, ktorý je daný súradnicou r bodu A₄.

V mnohých aplikáciách môže byť účinný potenciál spracovaný presne tak, ako potenciálna energia jednorozmerného systému: napríklad energetický diagram využívajúci efektívny potenciál určuje body obratu a polohy stabilnej a nestabilnej rovnováhy. Podobná metóda môže byť použitá aj v iných aplikáciách, napríklad v určovaní orbity vo všeobecnej relativistickej metrológii Schwarzschild.