Podmíněná entropie

Podmíněná entropie (anglicky conditional entropy) v teorii informace kvantifikuje množství informace potřebné pro popsání výsledku náhodného pokusu $Y$ , pokud je známá hodnota jiné náhodné proměnné $X$ . Měří se stejně jako informační entropie v bitech (kterým se v této souvislosti také říká „shannons“), někdy v „přirozených jednotkách“ (natech) nebo v desítkových číslicích (nazývaný „dits“, „bans“ nebo „hartleys“). Jednotka měření závisí na základu logaritmu použitého pro výpočet entropie.

Vennův diagram ukazující aditivní a subtraktivní vztahy různých informačních měr přiřazených ke korelovaným proměnným

X

a

Y

. Plocha pokrytá některou z kružnic je sdružená entropie

\mathrm {H} (X,Y)

. Kružnice vlevo (červená a fialová) je entropie

\mathrm {H} (X)

, přičemž červená je podmíněná entropie

\mathrm {H} (X|Y)

. Kružnice vpravo (modrá a fialová) je

\mathrm {H} (Y)

, přičemž modrá je

\mathrm {H} (Y|X)

. Fialová je vzájemná informace

\operatorname {I} (X;Y)

.

Entropii $Y$ podmíněnou $X$ zapisujeme $\mathrm {H} (Y|X)$ , kde $\mathrm {H}$ je velké řecké písmeno Éta.

Definice

Podmíněná entropie $Y$ , je-li dáno $X$ , je definována jako

$\mathrm {H} (Y|X)\ =-\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)\log {\frac {p(x,y)}{p(x)}}$

(1)

kde ${\mathcal {X}}$ a ${\mathcal {Y}}$ označuje nosič náhodných proměnných $X$ a $Y$ .

Poznámka: při výpočtech se neurčité výrazy $0\log 0$ a $0\log c/0$ pro pevné $c>0$ považují za rovné nule, protože $\lim _{\theta \to 0^{+}}\theta \,\log \,c/\theta =0$ a $\lim _{\theta \to 0^{+}}\theta \,\log \theta =0$ .[1]

Intuitivní vysvětlení definice: Podle definice platí, že $\displaystyle H(Y|X)=\mathbb {E} (\ f(X,Y)\ )$ kde $\displaystyle f:(x,y)\ \rightarrow -\log(\ p(y|x)\ ).$ $\displaystyle f$ přiřazuje dvojici $\displaystyle (x,y)$ informační obsah $\displaystyle (Y=y)$ , je-li dáno $\displaystyle (X=x)$ , což je množství informace potřebné pro popsání události $\displaystyle (Y=y)$ , je-li dáno $(X=x)$ . Podle zákona velkýich čísel, $\displaystyle H(Y|X)$ je aritmetický průměr velkého počtu nezávislých realizací $\displaystyle f(X,Y)$ .

Motivace

Nechť $\mathrm {H} (Y|X=x)$ je entropie diskrétní náhodné proměnné $Y$ podmíněná tím, že diskrétní náhodná proměnná $X$ nabývá hodnotu $x$ . Označme nosiče funkcí $X$ a $Y$ ${\mathcal {X}}$ a ${\mathcal {Y}}$ . Nechť $Y$ má pravděpodobnostní funkci $p_{Y}{(y)}$ . Nepodmíněná entropie $Y$ se spočítá jako $\mathrm {H} (Y):=\mathbb {E} [\operatorname {I} (Y)]$ , tj.

\mathrm {H} (Y)=\sum _{y\in {\mathcal {Y}}}{\mathrm {Pr} (Y=y)\,\mathrm {I} (y)}=-\sum _{y\in {\mathcal {Y}}}{p_{Y}(y)\log _{2}{p_{Y}(y)}},

kde $\operatorname {I} (y_{i})$ je informační obsah toho, že výsledek $Y$ má hodnotu $y_{i}$ . Entropie $Y$ podmíněná tím, že $X$ nabývá hodnotu $x$ , je definována podobně podmíněné očekávání:

\mathrm {H} (Y|X=x)=-\sum _{y\in {\mathcal {Y}}}{\Pr(Y=y|X=x)\log _{2}{\Pr(Y=y|X=x)}}.

Pamatujte, že $\mathrm {H} (Y|X)$ je výsledek průměrování $\mathrm {H} (Y|X=x)$ přes všechny možné hodnoty $x$ , kterých může nabývat $X$ . Také pokud se výše uvedený součet bere přes vzorek $y_{1},\dots ,y_{n}$ , očekávaná hodnota $E_{X}[\mathrm {H} (y_{1},\dots ,y_{n}\mid X=x)]$ je známa v nějakém oboru jako ekvivokace (anglicky equivocation).[2]

Jsou-li dány diskrétní náhodné proměnné $X$ s obrazem ${\mathcal {X}}$ a $Y$ s obrazem ${\mathcal {Y}}$ , podmíněná entropie $Y$ , je-li dáno $X$ se definuje jako vážený součet $\mathrm {H} (Y|X=x)$ pro každou možnou hodnotu $x$ , s použitím $p(x)$ jako váhy:[3]^:s.15

{\begin{aligned}\mathrm {H} (Y|X)\ &\equiv \sum _{x\in {\mathcal {X}}}\,p(x)\,\mathrm {H} (Y|X=x)\\&=-\sum _{x\in {\mathcal {X}}}p(x)\sum _{y\in {\mathcal {Y}}}\,p(y|x)\,\log \,p(y|x)\\&=-\sum _{x\in {\mathcal {X}}}\sum _{y\in {\mathcal {Y}}}\,p(x,y)\,\log \,p(y|x)\\&=-\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)\log \,p(y|x)\\&=-\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)\log {\frac {p(x,y)}{p(x)}}.\\&=\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)\log {\frac {p(x)}{p(x,y)}}.\\\end{aligned}}

Vlastnosti

Nulová podmíněná entropie

$\mathrm {H} (Y|X)=0$ právě tehdy, když hodnota $Y$ je úplně určena hodnotou $X$ .

Podmíněná entropie of nezávislý náhodné proměnné

Naopak $\mathrm {H} (Y|X)=\mathrm {H} (Y)$ právě tehdy, když $Y$ a $X$ jsou nezávislé náhodné proměnné.

Řetízkové pravidlo

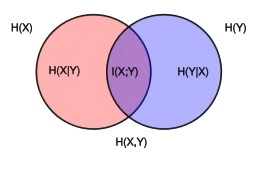
Předpokládejme, že kombinovaný systém určený dvěma náhodnými proměnnými $X$ a $Y$ má sdruženou entropii $\mathrm {H} (X,Y)$ , tj. potřebujeme průměrně $\mathrm {H} (X,Y)$ bitů informace pro popsání jeho přesného stavu. Pokud nejdříve zjistíme hodnotu $X$ , získali jsme $\mathrm {H} (X)$ bitů informace. Pokud je $X$ známé, potřebujeme pouze $\mathrm {H} (X,Y)-\mathrm {H} (X)$ bitů pro popsání stavu celého systému. Tato hodnota se přesně rovná $\mathrm {H} (Y|X)$ , kterou dává řetízkové pravidlo podmíněné entropie:

\mathrm {H} (Y|X)\,=\,\mathrm {H} (X,Y)-\mathrm {H} (X).

[3]^:s.17

řetízkové pravidlo vyplývá z výše uvedené definice podmíněné entropie:

{\begin{aligned}\mathrm {H} (Y|X)&=\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)\log \left({\frac {p(x)}{p(x,y)}}\right)\\[4pt]&=\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)(\log(p(x))-\log(p(x,y)))\\[4pt]&=-\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)\log(p(x,y))+\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}{p(x,y)\log(p(x))}\\[4pt]&=\mathrm {H} (X,Y)+\sum _{x\in {\mathcal {X}}}p(x)\log(p(x))\\[4pt]&=\mathrm {H} (X,Y)-\mathrm {H} (X).\end{aligned}}

Řetízkové pravidlo platí obecně pro více náhodné proměnné:

\mathrm {H} (X_{1},X_{2},\ldots ,X_{n})=\sum _{i=1}^{n}\mathrm {H} (X_{i}|X_{1},\ldots ,X_{i-1})

[3]^:s.22

Tento vztah se podobá řetízkovému pravidlu z teorie pravděpodobnosti, ale místo násobení využívá sčítání.

Bayesovo pravidlo

Bayesovo pravidlo pro podmíněnou entropii říká

\mathrm {H} (Y|X)\,=\,\mathrm {H} (X|Y)-\mathrm {H} (X)+\mathrm {H} (Y).

Důkaz: $\mathrm {H} (Y|X)=\mathrm {H} (X,Y)-\mathrm {H} (X)$ a $\mathrm {H} (X|Y)=\mathrm {H} (Y,X)-\mathrm {H} (Y)$ . Symetrie má za následek $\mathrm {H} (X,Y)=\mathrm {H} (Y,X)$ . Odečtením obou rovnic dostaneme Bayesovo pravidlo.

Pokud $Y$ je podmíněně nezávislé na $Z$ , je-li dáno $X$ máme:

\mathrm {H} (Y|X,Z)\,=\,\mathrm {H} (Y|X).

Další vlastnosti

Pro jakékoli $X$ a $Y$ :

{\begin{aligned}\mathrm {H} (Y|X)&\leq \mathrm {H} (Y)\,\\\mathrm {H} (X,Y)&=\mathrm {H} (X|Y)+\mathrm {H} (Y|X)+\operatorname {I} (X;Y),\qquad \\\mathrm {H} (X,Y)&=\mathrm {H} (X)+\mathrm {H} (Y)-\operatorname {I} (X;Y),\,\\\operatorname {I} (X;Y)&\leq \mathrm {H} (X),\,\end{aligned}}

kde $\operatorname {I} (X;Y)$ je vzájemná informace mezi $X$ a $Y$ .

Pro nezávislé $X$ a $Y$ :

\mathrm {H} (Y|X)=\mathrm {H} (Y)

a

\mathrm {H} (X|Y)=\mathrm {H} (X)\,

Přestože určitá podmíněná entropie $\mathrm {H} (X|Y=y)$ může být menší i větší než $\mathrm {H} (X)$ pro dané náhodné variace $y$ $Y$ , $\mathrm {H} (X|Y)$ nemůže nikdy přesáhnout $\mathrm {H} (X)$ .

Podmíněná diferenciální entropie

Definice

Výše uvedená definice platí pro diskrétní náhodné proměnné. Spojitá verze diskrétní podmíněné entropie se nazývá podmíněná diferenciální (nebo spojitá) entropie. Nechť $X$ a $Y$ jsou spojité náhodné proměnné se sdruženou hustotou pravděpodobnosti $f(x,y)$ . Diferenciální podmíněná entropie $h(X|Y)$ se definuje takto[3]^:s.249

$h(X|Y)=-\int _{{\mathcal {X}},{\mathcal {Y}}}f(x,y)\log f(x|y)\,dxdy$

(2)

Vlastnosti

Oproti podmíněné entropii pro diskrétní náhodné proměnné může být podmíněná diferenciální entropie záporná.

Stejně jako v diskrétním případě platí řetízkové pravidlo pro diferenciální entropii:

h(Y|X)\,=\,h(X,Y)-h(X)

[3]^:s.253

Toto pravidlo však neplatí, pokud se příslušné diferenciální entropie neexistují nebo jsou nekonečné.

Sdružené diferenciální entropie se také používají v definici vzájemné informace mezi spojitými náhodnými proměnnými:

\operatorname {I} (X,Y)=h(X)-h(X|Y)=h(Y)-h(Y|X)

$h(X|Y)\leq h(X)$ , přičemž rovnost nastává právě tehdy, když $X$ a $Y$ jsou nezávislé.[3]^:s.253

Vztah k chybě odhad

Podmíněné diferenciální entropie dává spodní mez očekávané druhé mocniny chyby odhadu. Pro jakoukoli náhodnou proměnnou $X$ , pozorování $Y$ a odhad ${\widehat {X}}$ platí:[3]^:s.255

\mathbb {E} \left[{\bigl (}X-{\widehat {X}}{(Y)}{\bigr )}^{2}\right]\geq {\frac {1}{2\pi e}}e^{2h(X|Y)}

Což se podobá principu neurčitosti z kvantové mechaniky.

Zobecnění na kvantovou teorii

V kvantové teorii informace se podmíněná entropie zobecňuje na podmíněnou kvantovou entropii, která na rozdíl od svého klasického protějšku může nabývat záporných hodnot.

Odkazy

Reference

V tomto článku byl použit překlad textu z článku Conditional entropy na anglické Wikipedii.

David MacKay: Information Theory, Pattern Recognition and Neural Networks: The Book [online]. [cit. 2019-10-25]. Dostupné online.
HELLMAN, M.; RAVIV, J. Probability of error, equivocation, and the Chernoff bound. IEEE Transactions on Information Theory. 1970, roč. 16, čís. 4, s. 368–372.
COVER, Thomas M. Elements of Information Theory. [s.l.]: [s.n.], 1991. Dostupné online. ISBN 0-471-06259-6.

Související články

Informační entropie
Vzájemná informace
Podmíněná kvantová entropie
Věrohodnostní funkce

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] David MacKay: Information Theory, Pattern Recognition and Neural Networks: The Book [online]. [cit. 2019-10-25]. Dostupné online.

[2] HELLMAN, M.; RAVIV, J. Probability of error, equivocation, and the Chernoff bound. IEEE Transactions on Information Theory. 1970, roč. 16, čís. 4, s. 368–372.

[cover1991-3] COVER, Thomas M. Elements of Information Theory. [s.l.]: [s.n.], 1991. Dostupné online. ISBN 0-471-06259-6.